Capítulo 11 Análise de Variância para 2 fatores

Também conhecida como 2-way Anova, é utilizada quando um estudo ou experimento é desenhado para responder a mais questões que uma Anova para 1 fator é capaz de responder.

É muito comum comparar tratamentos que são combinações de dois fatores independentes.

A inferência para uma Anova de dois fatores é feita da seguinte forma:

Faça gráficos das médias dos grupos

Procure por interação
Procure por efeitos principais

Faça o teste F para três questões:

Há interação?
Há efeito principal para o primeiro fator?
Há efeito principal para o segundo fator?

A seguir veremos três exemplos que ilustram várias situações da Anova de 2 fatores.

Exemplo 11.1 (Análise de Variância para dois fatores - interação não significativa) A reprodução tem um custo fisiológico alto. Uma dieta rica em proteínas pode aumentar a capacidade reprodutiva de moscas das frutas.

Um experimento avaliou a porcentagem de gordura corporal em 40 fêmeas de mosca das frutas alimentadas com 4 dietas enriquecidas com proteínas (ou não) nas doses de 0, 1, 3 e 7 g.

O experimento usou moscas selvagens e mutantes com ciclo reprodutivo mais longo.

A resposta foi a porcentagem de gordura corporal após duas semanas da dieta, contidas no arquivo mosca.xlsx.

São três grupos de hipóteses a serem testadas:

H₀: não há interação entre os genótipos e quantidade de proteína na porcentagem de gordura corporal de moscas.
H₁: há interação entre os genótipos e quantidade de proteína na porcentagem de gordura corporal de moscas.
H₀: a quantidade de proteína não influencia na porcentagem de gordura corporal de moscas.
H₁:a quantidade de proteína influencia na porcentagem de gordura corporal de moscas.
H₀: o genótipo não influencia na porcentagem de gordura corporal de moscas.
H₁: o genótipo influencia na porcentagem de gordura corporal de moscas.

Análise exploratória:

mosca <- readxl::read_excel("data/mosca.xlsx") %>%
  mutate(
    genotipo = factor(genotipo),
    proteina = factor(proteina)
  )


mosca %>%
  group_by(genotipo, proteina) %>%
  summarise(
    n = n(),
    media = mean(gordura),
    desvpad = sd(gordura),
    var = var(gordura)
  )

## `summarise()` has grouped output by 'genotipo'. You can override using the
## `.groups` argument.

## # A tibble: 8 × 6
## # Groups:   genotipo [2]
##   genotipo proteina     n media desvpad    var
##   <fct>    <fct>    <int> <dbl>   <dbl>  <dbl>
## 1 mutante  0            5  24.2   1.76   3.09 
## 2 mutante  1            5  23.3   2.51   6.32 
## 3 mutante  3            5  14.6   3.17  10.1  
## 4 mutante  7            5  13.0   2.71   7.33 
## 5 selvagem 0            5  25.6   1.50   2.24 
## 6 selvagem 1            5  22.3   1.72   2.96 
## 7 selvagem 3            5  15.1   0.691  0.477
## 8 selvagem 7            5  11.6   1.06   1.13

## Boxplot - Efeito principal fator A
boxplot(gordura ~ genotipo, data = mosca)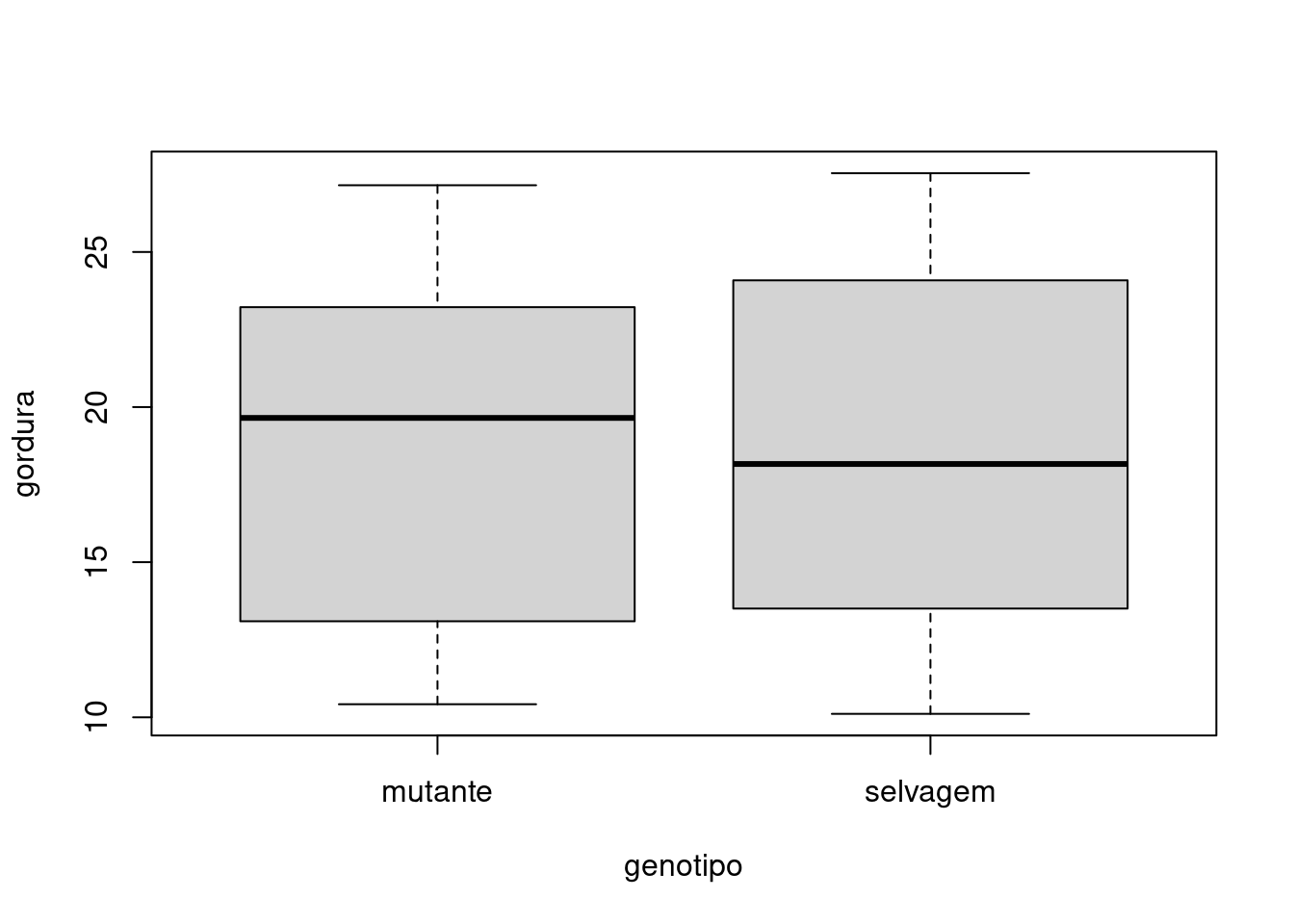

## Boxplot - Efeito principal fator B
boxplot(gordura ~ proteina, data = mosca)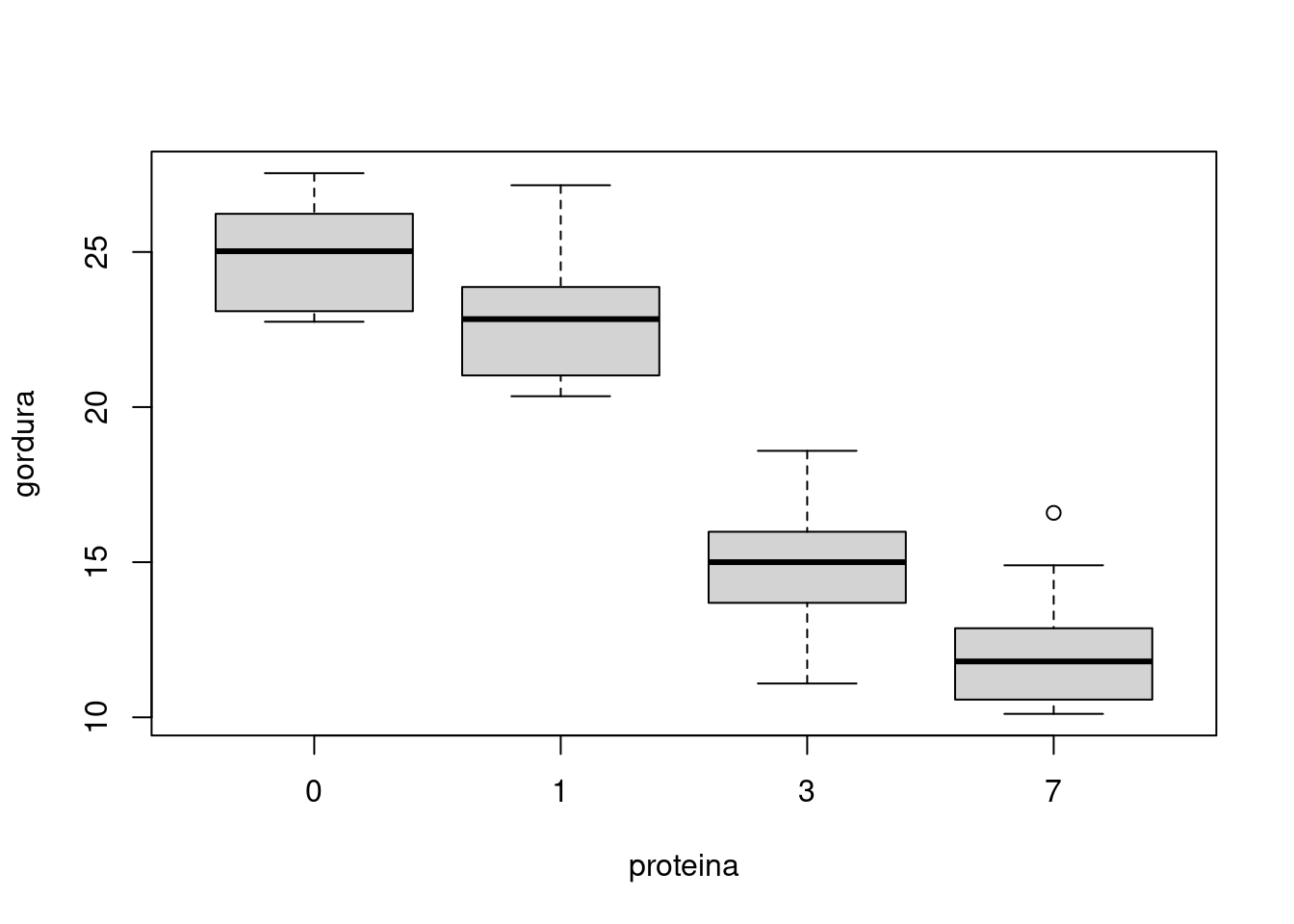

## Boxplot - Interação
boxplot(gordura ~ genotipo * proteina, data = mosca)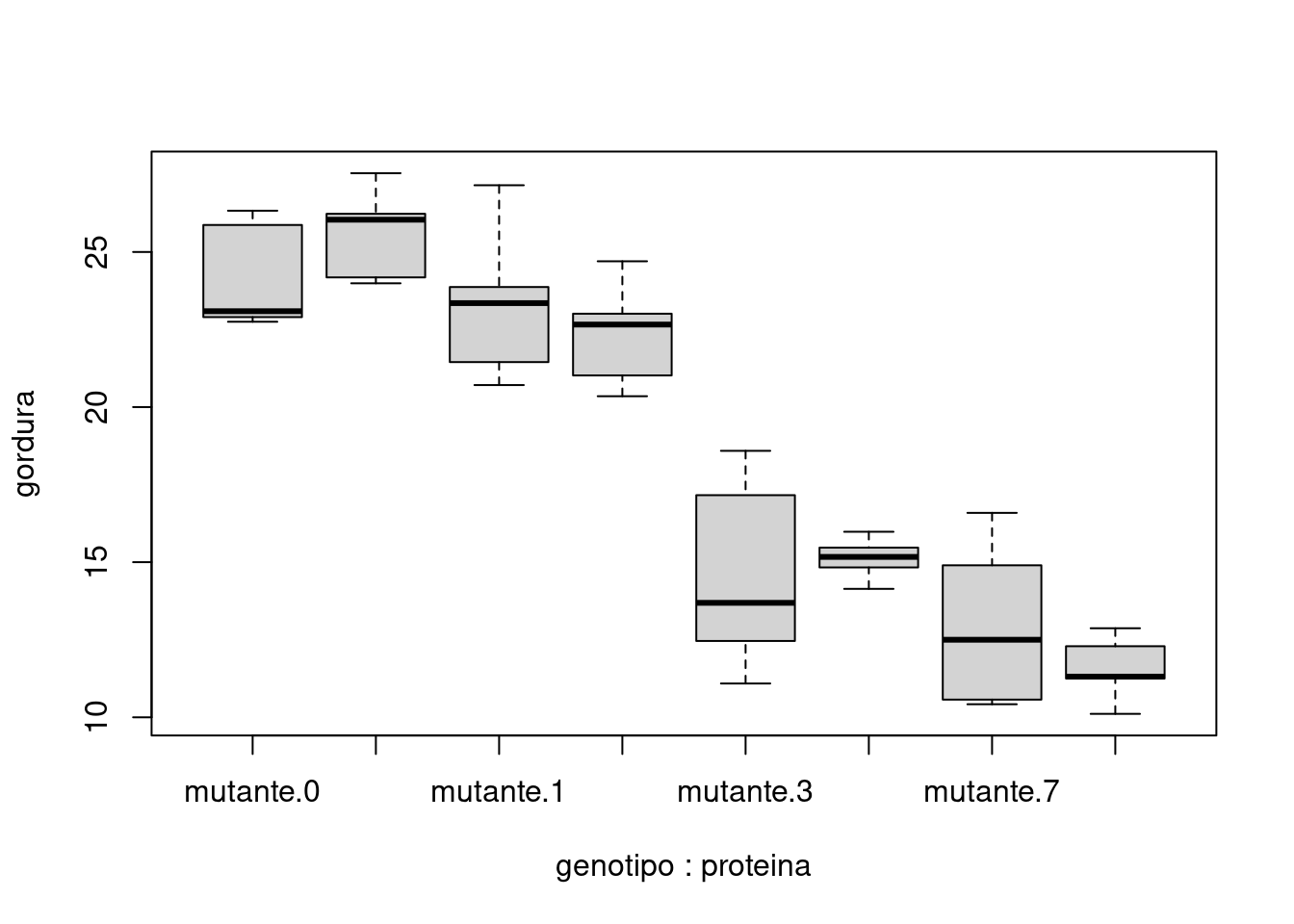

## Gráfico da interação
with(mosca, interaction.plot(genotipo, proteina, gordura))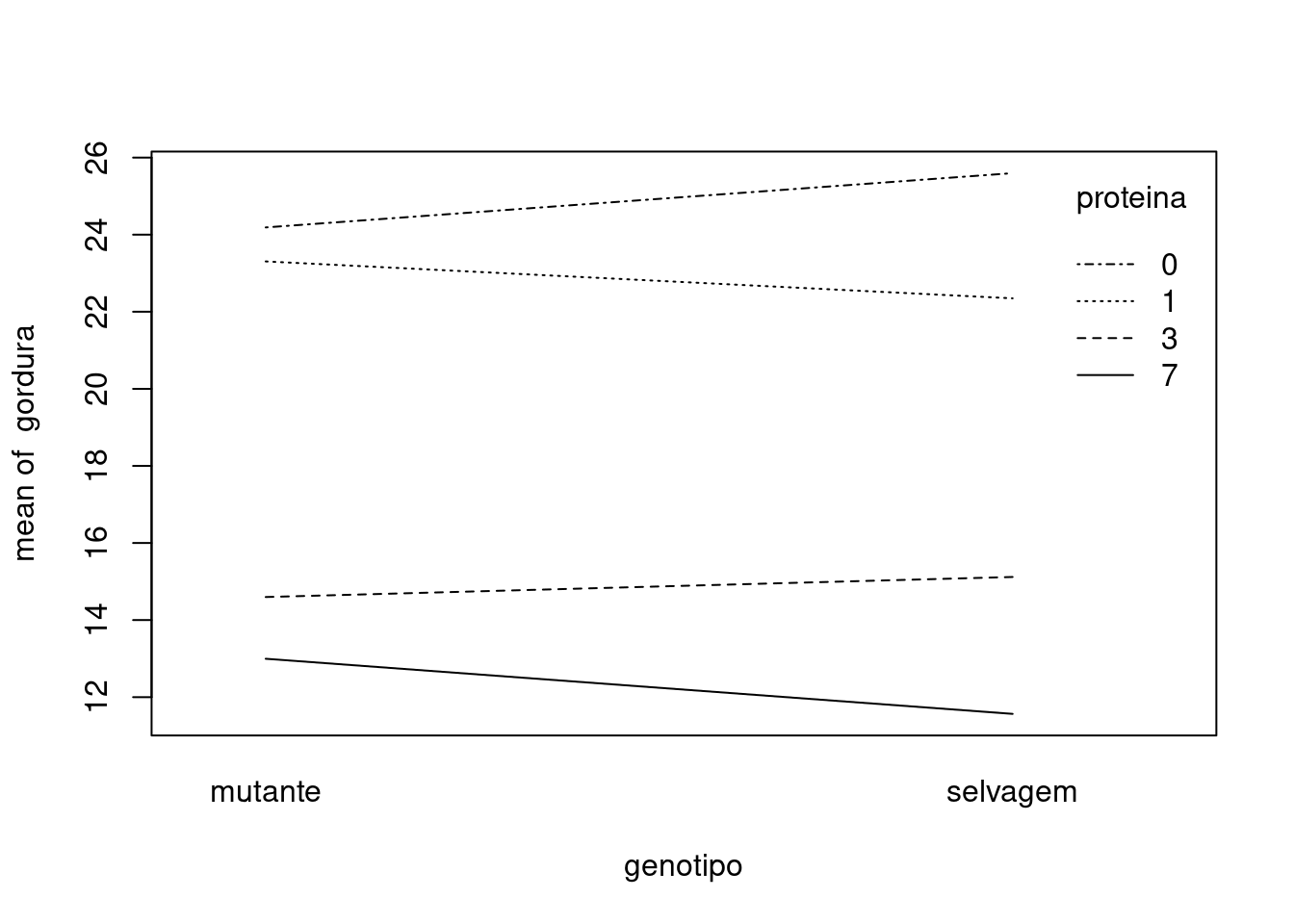

with(mosca, interaction.plot(proteina, genotipo, gordura))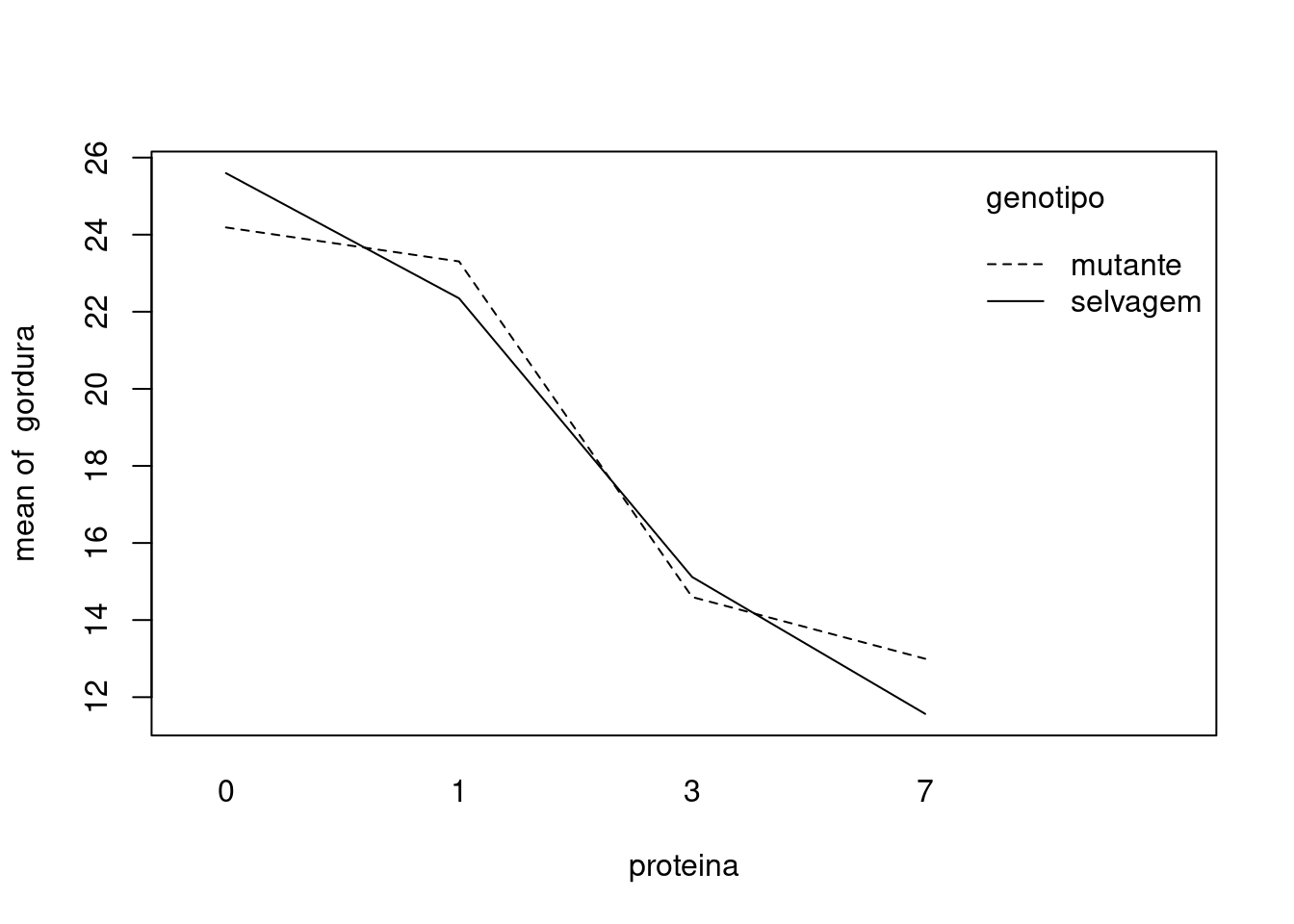

Efetuamos a Análise de Variância para os efeitos principais e para a interação:

aov_mosca <- lm(gordura ~ genotipo * proteina, data = mosca)

anova(aov_mosca)

## Analysis of Variance Table
## 
## Response: gordura
##                   Df  Sum Sq Mean Sq F value    Pr(>F)    
## genotipo           1    0.13    0.13  0.0315    0.8602    
## proteina           3 1113.37  371.12 88.3984 1.429e-15 ***
## genotipo:proteina  3   12.91    4.30  1.0247    0.3947    
## Residuals         32  134.35    4.20                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

A interação (p-valor=0,395) e o efeito principal para genótipo (p-valor=0,86) são pequenos (não significativos). O efeito principal para proteína (p-valor < 0,001) é grande (significativo).

Verificação do presuposto da Normalidade.

## curtose
aov_mosca %>%
  residuals() %>%
  moments::kurtosis()

## [1] 2.495927

## assimetria
aov_mosca %>%
  residuals() %>%
  moments::skewness()

## [1] 0.3766119

## Teste de Shapiro-Wilk
aov_mosca %>%
  residuals() %>%
  shapiro.test()

## 
##  Shapiro-Wilk normality test
## 
## data:  .
## W = 0.97295, p-value = 0.444

## Gráfico dos quantis normais
aov_mosca %>%
  residuals() %>%
  qqnorm()
aov_mosca %>%
  residuals() %>%
  qqline()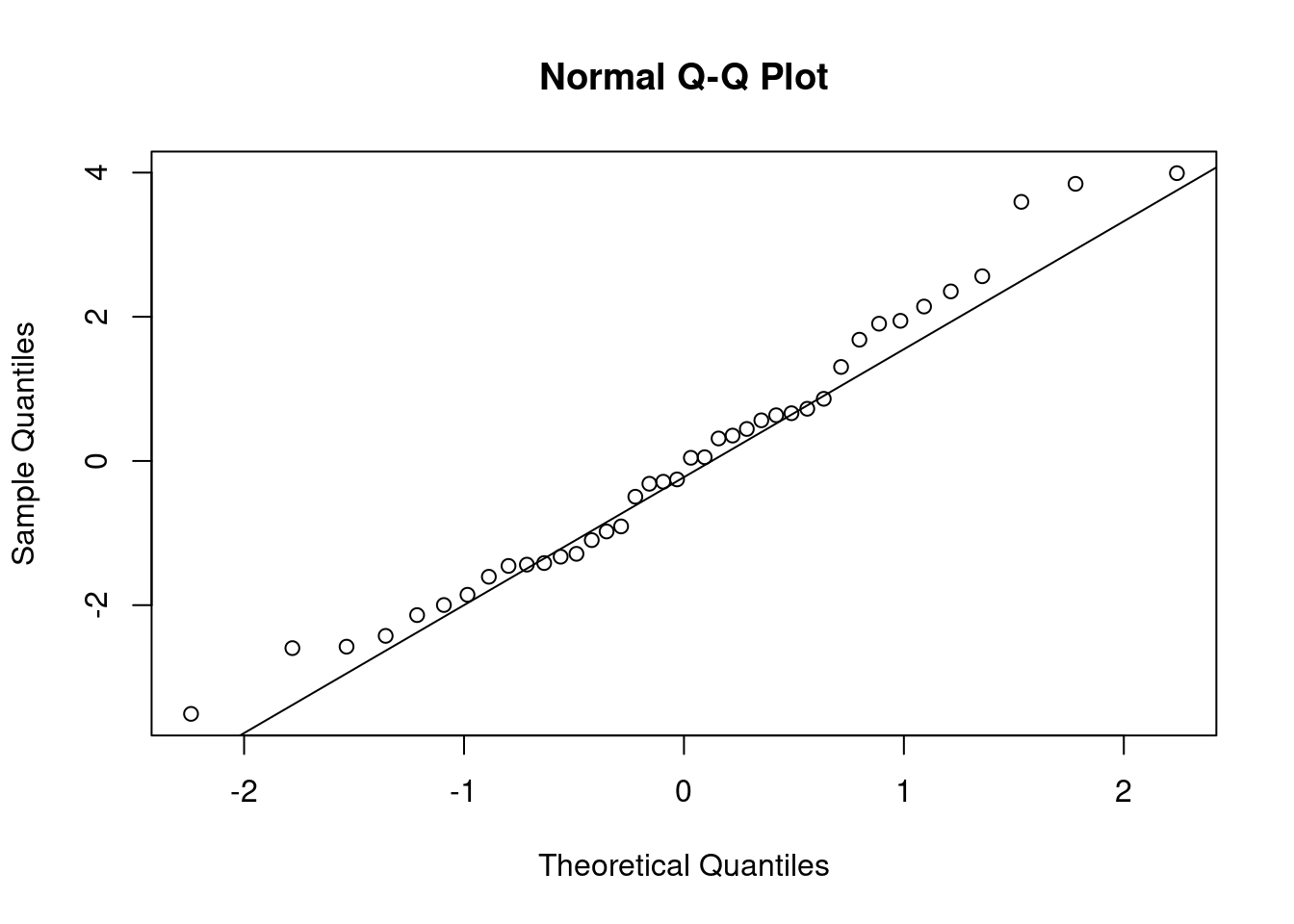

## Histograma
aov_mosca %>%
  residuals() %>%
  hist()

## Ramo e folhas
aov_mosca %>%
  residuals() %>%
  stem()

## 
##   The decimal point is at the |
## 
##   -3 | 5
##   -2 | 66410
##   -1 | 965443310
##   -0 | 95333
##    0 | 0134466779
##    1 | 3799
##    2 | 146
##    3 | 68
##    4 | 0

Verificação do presuposto da homogeneidade das variâncias

## razão maior/menor desvio-padrão
mosca %>%
  group_by(genotipo, proteina) %>%
  summarise(desvpad = sd(gordura)) %>%
  mutate(razao = max(desvpad) / desvpad)

## `summarise()` has grouped output by 'genotipo'. You can override using the
## `.groups` argument.

## # A tibble: 8 × 4
## # Groups:   genotipo [2]
##   genotipo proteina desvpad razao
##   <fct>    <fct>      <dbl> <dbl>
## 1 mutante  0          1.76   1.80
## 2 mutante  1          2.51   1.26
## 3 mutante  3          3.17   1   
## 4 mutante  7          2.71   1.17
## 5 selvagem 0          1.50   1.15
## 6 selvagem 1          1.72   1   
## 7 selvagem 3          0.691  2.49
## 8 selvagem 7          1.06   1.62

## boxplot condicional dos resíduos
boxplot(residuals(aov_mosca) ~ genotipo * proteina, data = mosca)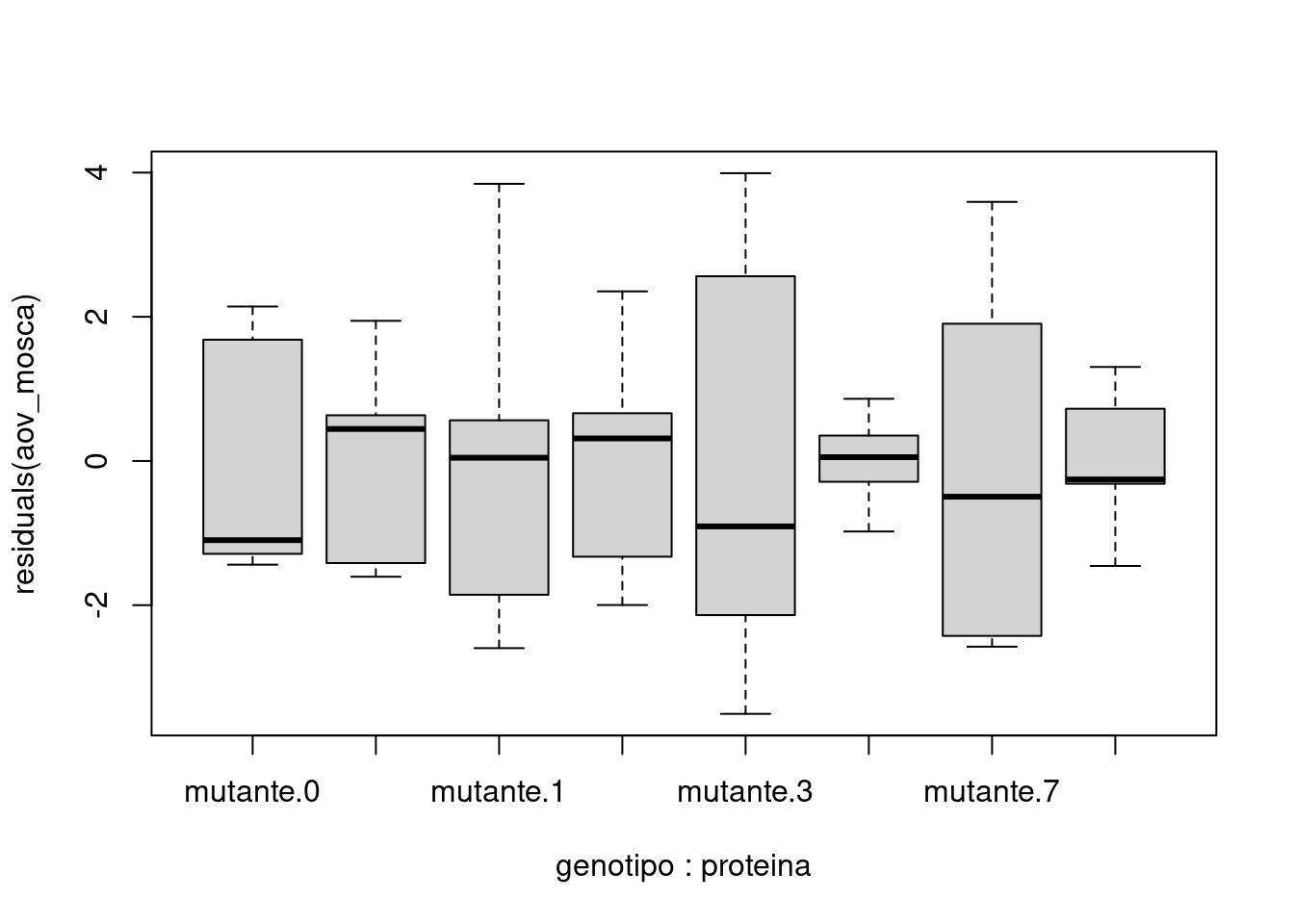

## resíduos vs ajustados
plot(aov_mosca, 1)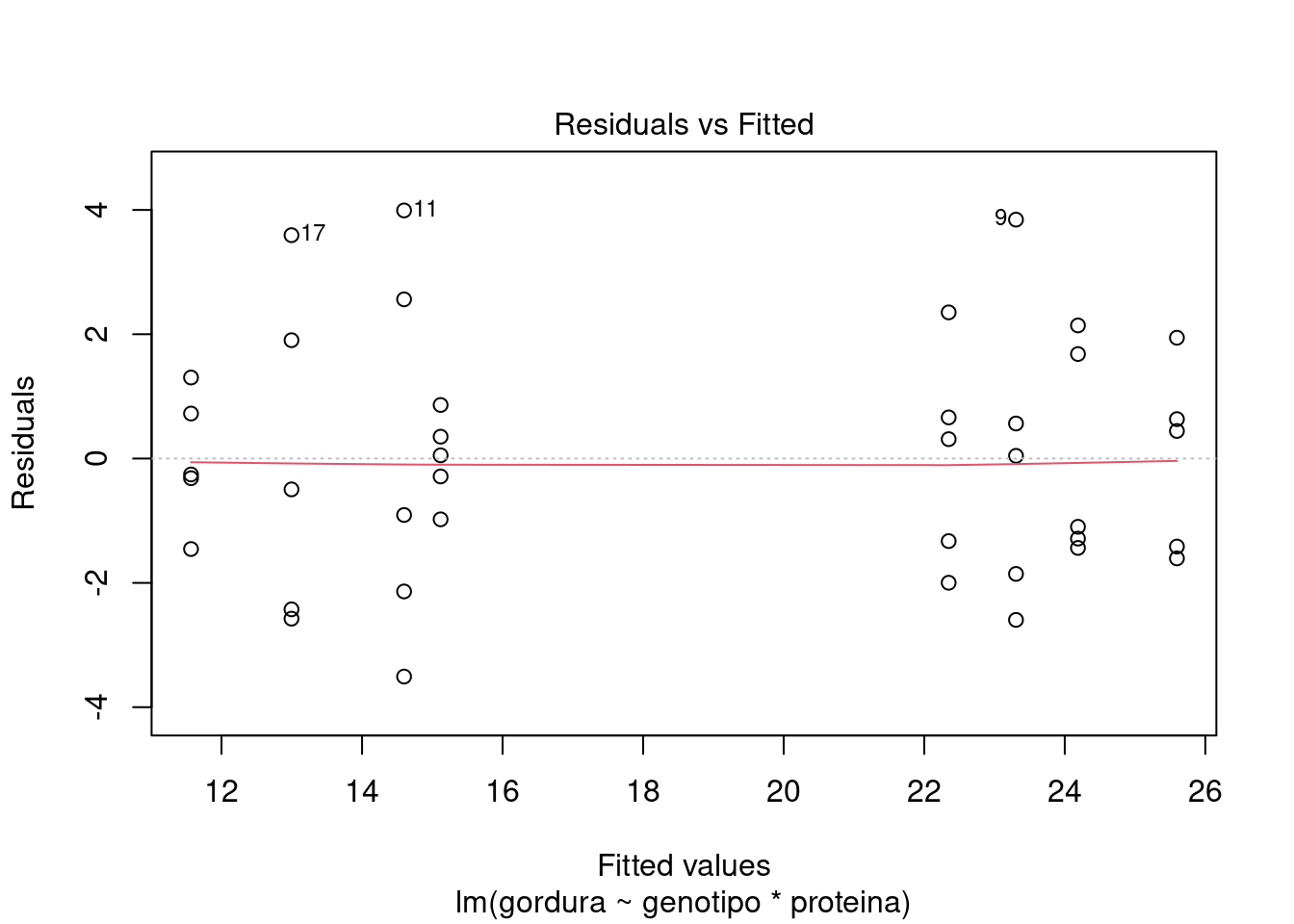

## teste de Bartlett
bartlett.test(residuals(aov_mosca) ~ paste0(genotipo, proteina), data = mosca)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  residuals(aov_mosca) by paste0(genotipo, proteina)
## Bartlett's K-squared = 10.739, df = 7, p-value = 0.1504

## teste de Levene
car::leveneTest(residuals(aov_mosca) ~ paste0(genotipo, proteina), data = mosca)

## Warning in leveneTest.default(y = y, group = group, ...): group coerced to
## factor.

## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value Pr(>F)
## group  7  1.3106 0.2773
##       32

Pela análise do conjunto dos resultados acima, não há evidência de violação dos pressupostos.

Teste de comparação de médias para o efeito principal do fator proteína:

tk_proteina <- emmeans::emmeans(aov_mosca, ~proteina, contr = "tukey")

## NOTE: Results may be misleading due to involvement in interactions

## contrastes
tk_proteina$contrasts

##  contrast              estimate    SE df t.ratio p.value
##  proteina0 - proteina1     2.06 0.916 32   2.254  0.1307
##  proteina0 - proteina3    10.03 0.916 32  10.950  <.0001
##  proteina0 - proteina7    12.61 0.916 32  13.763  <.0001
##  proteina1 - proteina3     7.97 0.916 32   8.697  <.0001
##  proteina1 - proteina7    10.55 0.916 32  11.509  <.0001
##  proteina3 - proteina7     2.58 0.916 32   2.812  0.0395
## 
## Results are averaged over the levels of: genotipo 
## P value adjustment: tukey method for comparing a family of 4 estimates

## Intervalo de confiança
tk_proteina$contrasts %>% confint()

##  contrast              estimate    SE df lower.CL upper.CL
##  proteina0 - proteina1     2.06 0.916 32  -0.4177     4.55
##  proteina0 - proteina3    10.03 0.916 32   7.5513    12.52
##  proteina0 - proteina7    12.61 0.916 32  10.1283    15.09
##  proteina1 - proteina3     7.97 0.916 32   5.4863    10.45
##  proteina1 - proteina7    10.55 0.916 32   8.0633    13.03
##  proteina3 - proteina7     2.58 0.916 32   0.0943     5.06
## 
## Results are averaged over the levels of: genotipo 
## Confidence level used: 0.95 
## Conf-level adjustment: tukey method for comparing a family of 4 estimates

## letras (CLD)
tk_proteina$emmeans %>% multcomp::cld(Letters = letters)

##  proteina emmean    SE df lower.CL upper.CL .group
##  7          12.3 0.648 32     11.0     13.6  a    
##  3          14.9 0.648 32     13.5     16.2   b   
##  1          22.8 0.648 32     21.5     24.1    c  
##  0          24.9 0.648 32     23.6     26.2    c  
## 
## Results are averaged over the levels of: genotipo 
## Confidence level used: 0.95 
## P value adjustment: tukey method for comparing a family of 4 estimates 
## significance level used: alpha = 0.05 
## NOTE: If two or more means share the same grouping symbol,
##       then we cannot show them to be different.
##       But we also did not show them to be the same.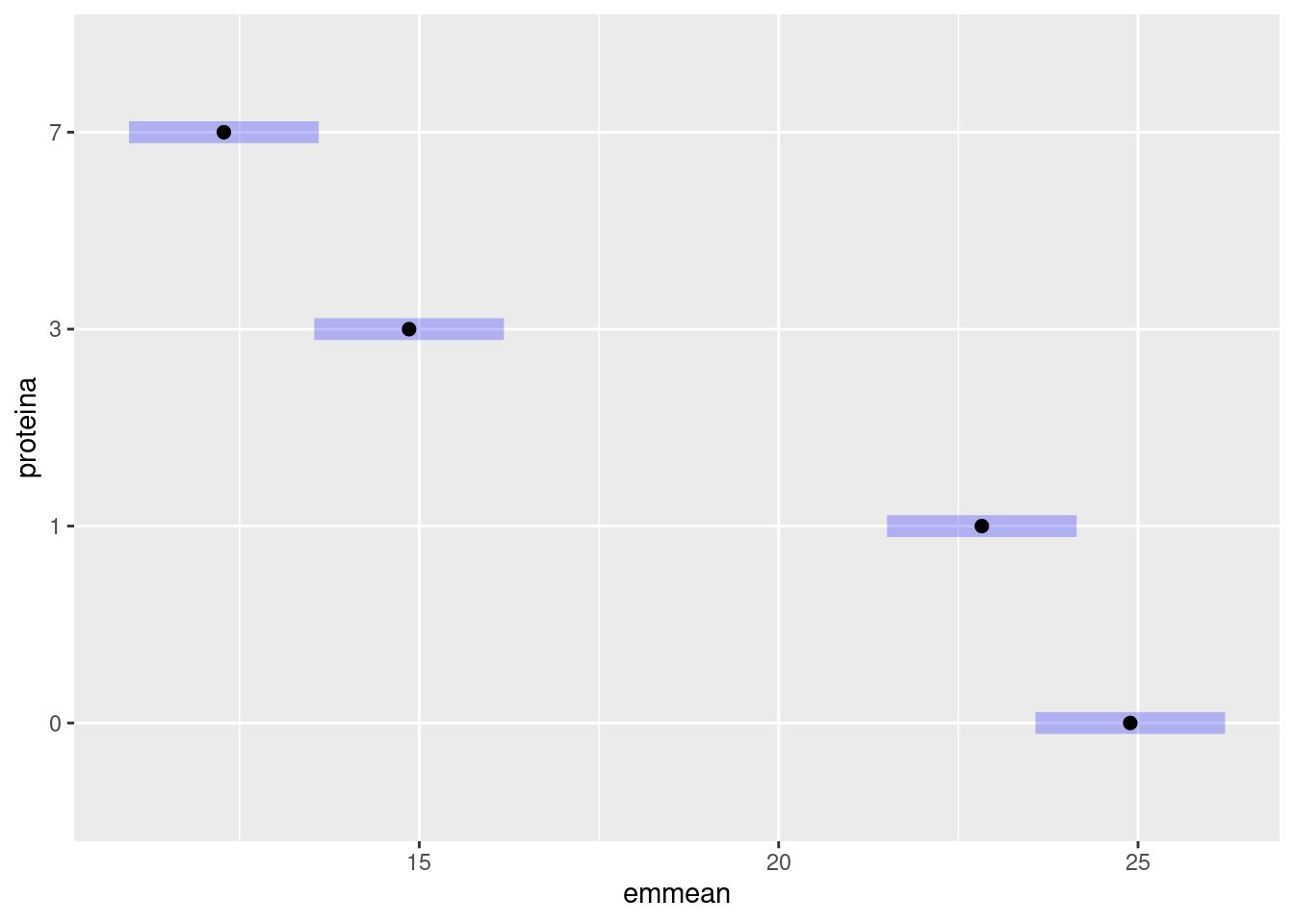

## plot
tk_proteina$emmeans %>% plot()

Teste de comparação de médias para o efeito principal do fator genótipo:

tk_genotipo <- emmeans::emmeans(aov_mosca, ~genotipo, contr = "tukey")

## NOTE: Results may be misleading due to involvement in interactions

## contrastes
tk_genotipo$contrasts

##  contrast           estimate    SE df t.ratio p.value
##  mutante - selvagem    0.115 0.648 32   0.177  0.8602
## 
## Results are averaged over the levels of: proteina

## Intervalo de confiança
tk_genotipo$contrasts %>% confint()

##  contrast           estimate    SE df lower.CL upper.CL
##  mutante - selvagem    0.115 0.648 32     -1.2     1.43
## 
## Results are averaged over the levels of: proteina 
## Confidence level used: 0.95

## letras (CLD)
tk_genotipo$emmeans %>% multcomp::cld(Letters = letters)

##  genotipo emmean    SE df lower.CL upper.CL .group
##  selvagem   18.7 0.458 32     17.7     19.6  a    
##  mutante    18.8 0.458 32     17.8     19.7  a    
## 
## Results are averaged over the levels of: proteina 
## Confidence level used: 0.95 
## significance level used: alpha = 0.05 
## NOTE: If two or more means share the same grouping symbol,
##       then we cannot show them to be different.
##       But we also did not show them to be the same.

## plot
tk_genotipo$emmeans %>% plot()

Conclusão: Maiores quantidade de proteína na dieta levam a menores taxas de gordura corporal. O genótipo da mosca das frutas tem um efeito pequeno na gordura corporal para qualquer quantidade de proteína.

O próximo exemplo ilustra uma situação em que a interação é significativa, mas os efeitos principais são grandes e mais importantes.

Exemplo 11.2 (Análise de Variância para dois fatores - interação significativa mas com efeitos principais grandes e mais importantes) Fungos micorrízicos estão presentes nas raízes de muitas plantas. Eles tem uma relação simbiótica com a planta.

Um experimento comparou o efeito da adição de nitrogênio em dois genótipos de tomate, um selvagem suscetível a micorrizas e um mutante não suscetível.

O nitrogênio foi adicionado nas doses de 0, 28 e 10 kg/ha.

Seis plantas foram aleatoriamente designadas a cada grupo.

A variável resposta é a porcentagem de fósforo nas plantas depois de 19 semanas (tomate.xlsx).

São três grupos de hipóteses a serem testadas:

H₀ : não há interação entre os genótipos e doses de nitrogênio na porcentagem de fósforo em plantas de tomate.
H₁: há interação entre os genótipos e doses de nitrogênio na porcentagem de fósforo em plantas de tomate.
H₀: o genótipo não influencia na porcentagem de fósforo em plantas de tomate.
H₁: o genótipo influencia na porcentagem de fósforo em plantas de tomate.
H₀: as doses de nitrogênio não influenciam na porcentagem de fósforo em plantas de tomate.
H₁: as doses de nitrogênio influenciam na porcentagem de fósforo em plantas de tomate.

Análise exploratória:

tomate <- readxl::read_excel("data/tomate.xlsx") %>%
  mutate(
    genotipo = factor(genotipo),
    nitrogenio = factor(nitrogenio)
  )


tomate %>%
  group_by(genotipo, nitrogenio) %>%
  summarise(
    n = n(),
    media = mean(fosforo),
    desvpad = sd(fosforo),
    var = var(fosforo)
  )

## `summarise()` has grouped output by 'genotipo'. You can override using the
## `.groups` argument.

## # A tibble: 6 × 6
## # Groups:   genotipo [2]
##   genotipo nitrogenio     n media desvpad      var
##   <fct>    <fct>      <int> <dbl>   <dbl>    <dbl>
## 1 mutante  0              6 0.248  0.0306 0.000937
## 2 mutante  28             6 0.207  0.0242 0.000587
## 3 mutante  160            6 0.182  0.0147 0.000217
## 4 selvagem 0              6 0.512  0.0833 0.00694 
## 5 selvagem 28             6 0.423  0.0455 0.00207 
## 6 selvagem 160            6 0.318  0.0462 0.00214

## Boxplot - Efeito principal fator A
boxplot(fosforo ~ genotipo, data = tomate)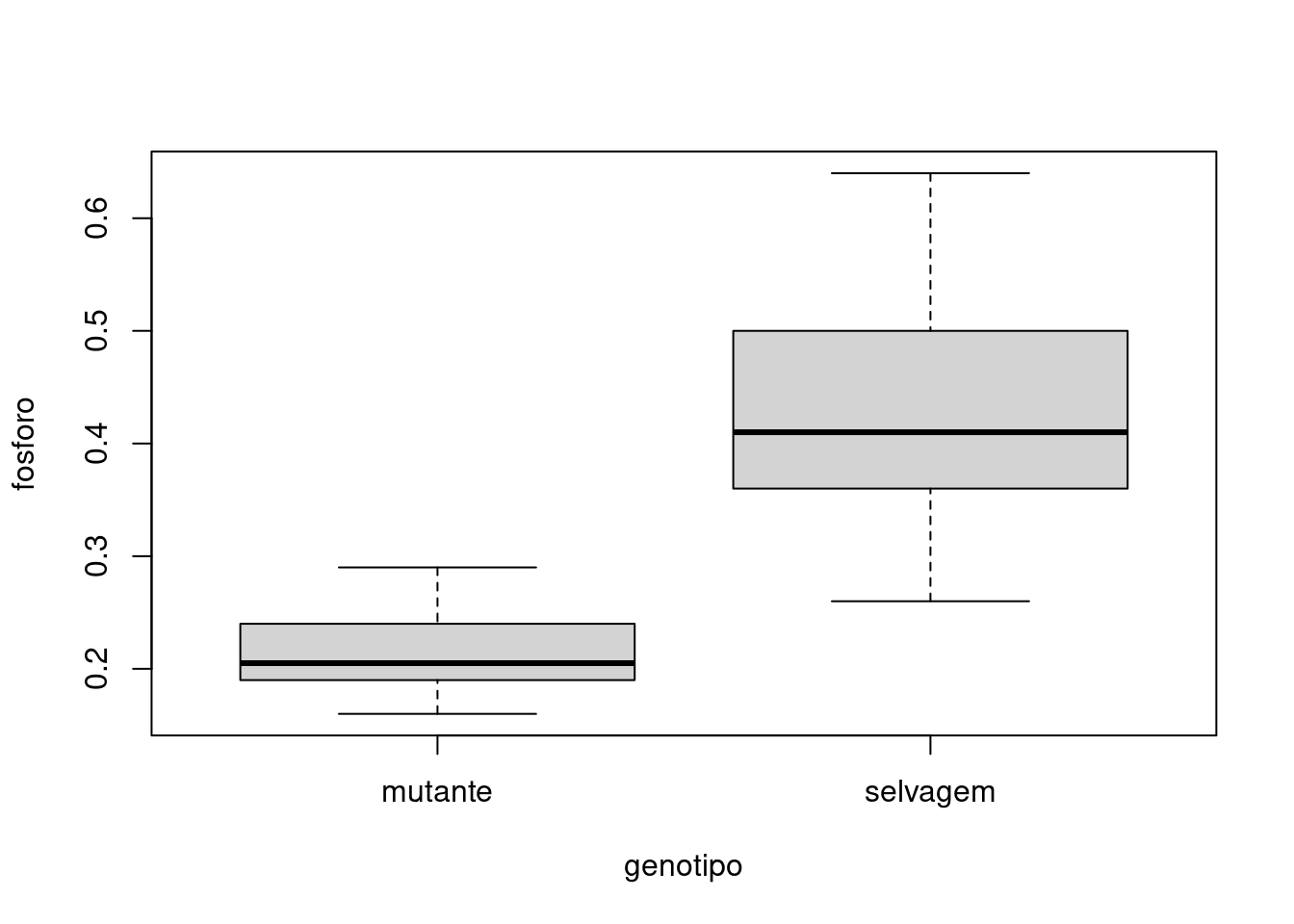

## Boxplot - Efeito principal fator B
boxplot(fosforo ~ nitrogenio, data = tomate)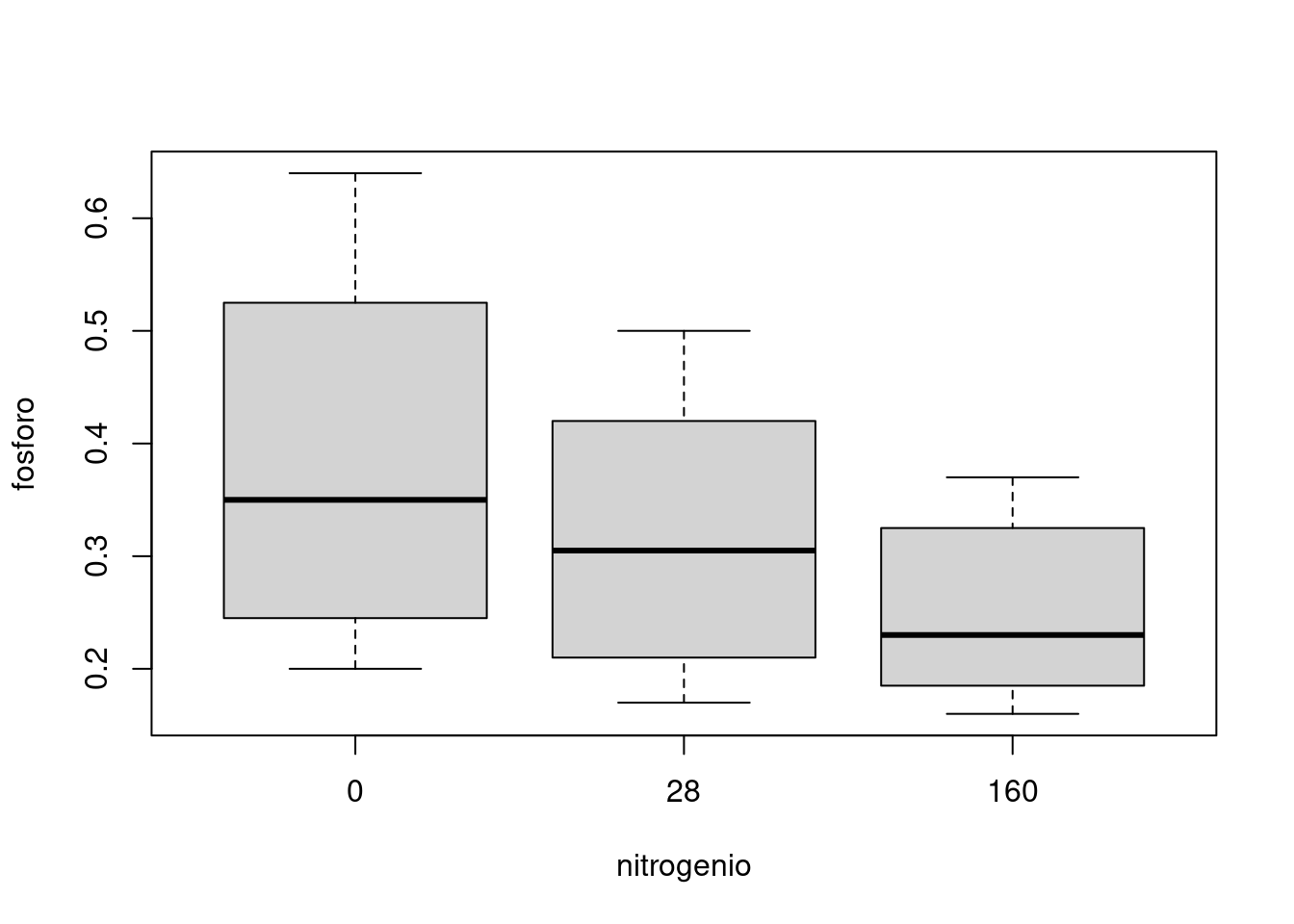

## Boxplot - Interação
boxplot(fosforo ~ genotipo * nitrogenio, data = tomate)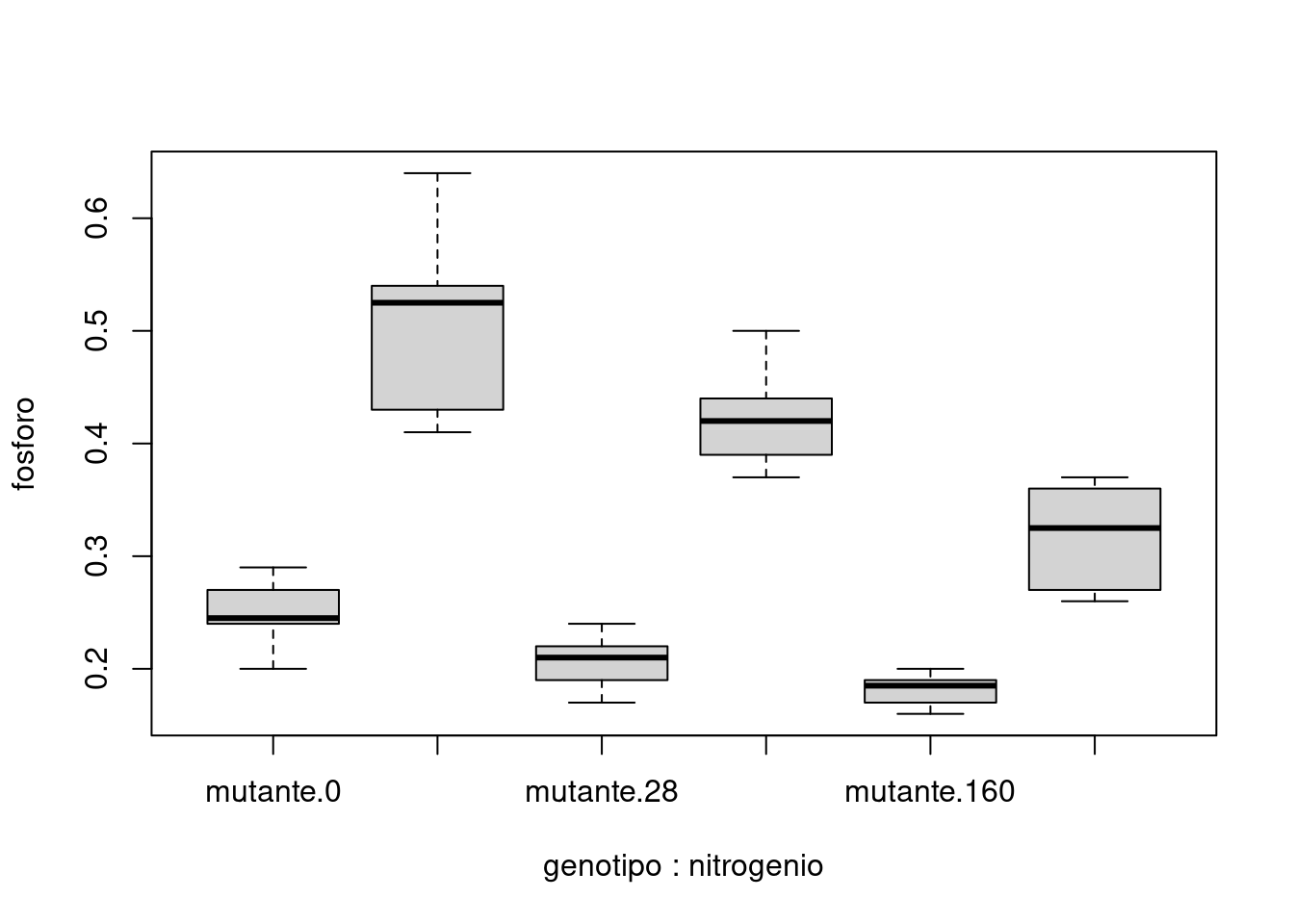

## Gráfico da interação
with(tomate, interaction.plot(genotipo, nitrogenio, fosforo))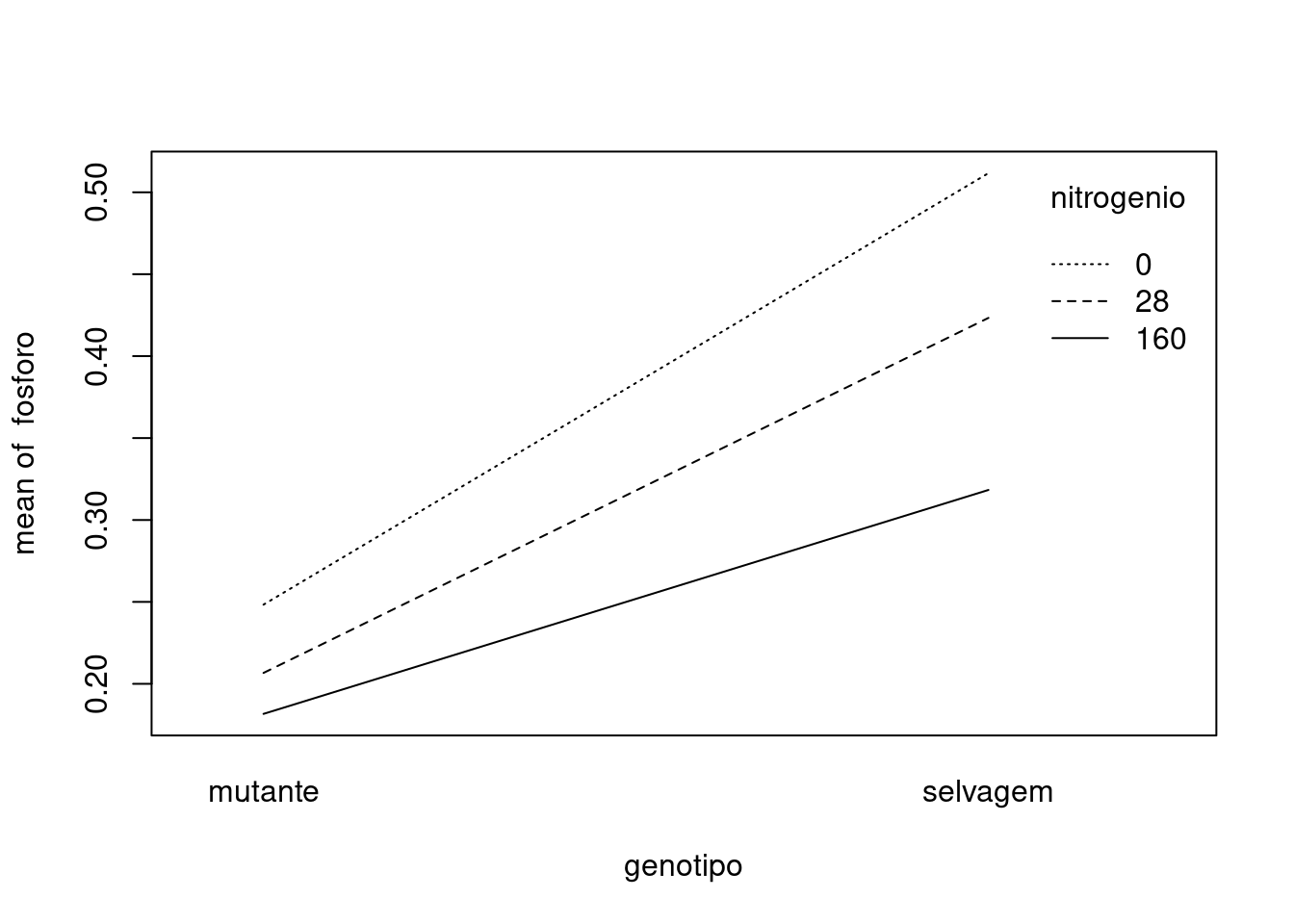

with(tomate, interaction.plot(nitrogenio, genotipo, fosforo))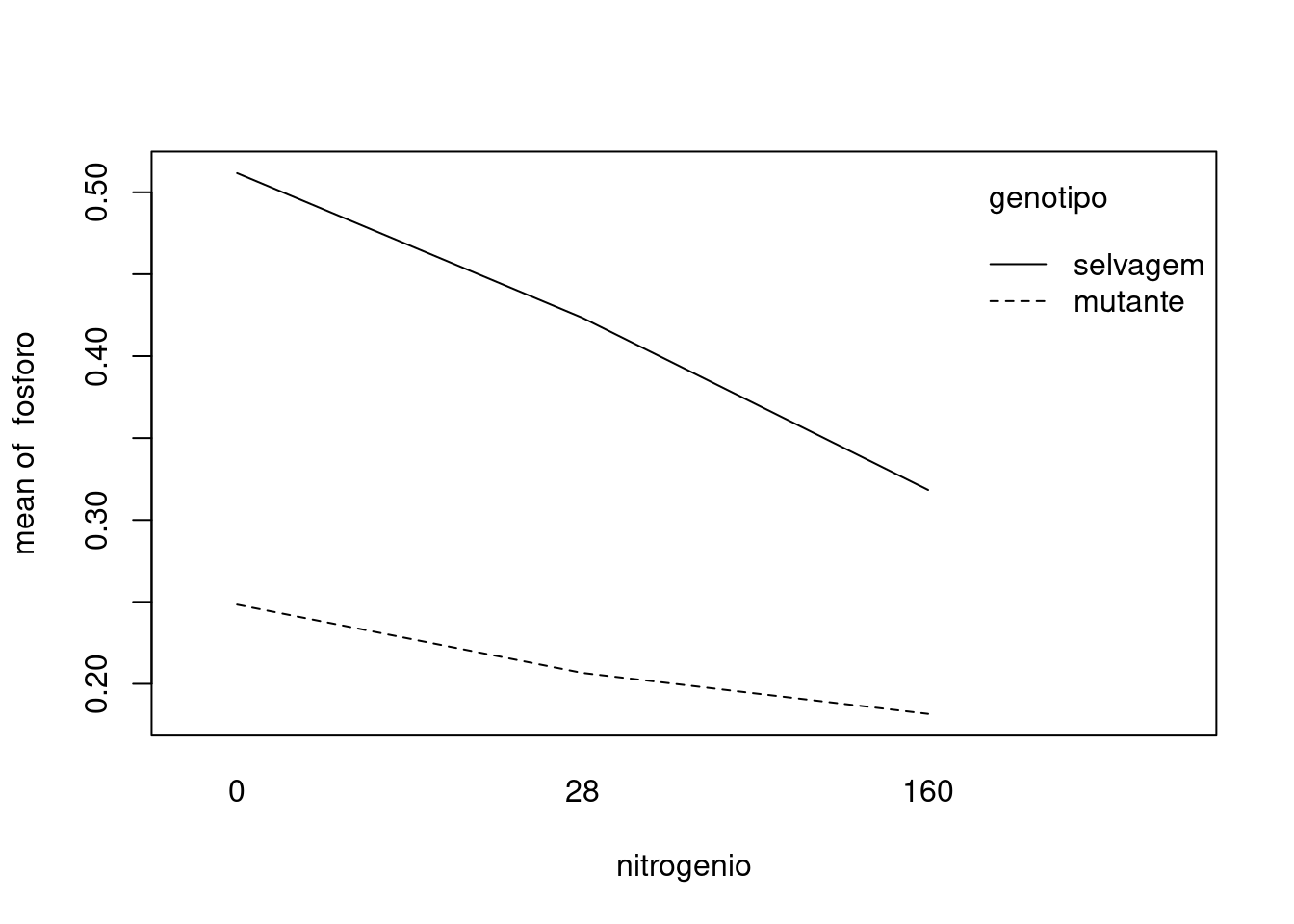

Efetuamos a Análise de Variância para os efeitos principais e para a interação:

aov_tomate <- lm(fosforo ~ genotipo * nitrogenio, data = tomate)

anova(aov_tomate)

## Analysis of Variance Table
## 
## Response: fosforo
##                     Df  Sum Sq Mean Sq F value    Pr(>F)    
## genotipo             1 0.38028 0.38028 177.148 4.019e-14 ***
## nitrogenio           2 0.10140 0.05070  23.618 6.911e-07 ***
## genotipo:nitrogenio  2 0.02462 0.01231   5.735  0.007777 ** 
## Residuals           30 0.06440 0.00215                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

A interação é significativa (p-valor = 0,0077), mas ela é pequena comparada com os efeitos principais.

O efeito principal para genótipos (p-valor < 0,001) nos mostra que tomates selvagens com micorrizas tem maiores níveis de fósforo para todas as doses de nitrogênio, devido ao benefício da simbiose.

O efeito principal para nitrogênio (p-valor < 0,001) mostra que os níveis de fósforo diminuem com o aumento da dose de nitrogênio.

Verificação dos presupostos da Normalidade e Homogeneidade das Variâncias (análise não mostrada): não há evidência de violação dos pressupostos.

Teste de comparação de médias para o efeito principal do fator nitrogênio:

tk_nitrogenio <- emmeans::emmeans(aov_tomate, ~nitrogenio, contr = "tukey")

## NOTE: Results may be misleading due to involvement in interactions

## contrastes
tk_nitrogenio$contrasts

##  contrast                     estimate     SE df t.ratio p.value
##  nitrogenio0 - nitrogenio28      0.065 0.0189 30   3.436  0.0048
##  nitrogenio0 - nitrogenio160     0.130 0.0189 30   6.873  <.0001
##  nitrogenio28 - nitrogenio160    0.065 0.0189 30   3.436  0.0048
## 
## Results are averaged over the levels of: genotipo 
## P value adjustment: tukey method for comparing a family of 3 estimates

## Intervalo de confiança
tk_nitrogenio$contrasts %>% confint()

##  contrast                     estimate     SE df lower.CL upper.CL
##  nitrogenio0 - nitrogenio28      0.065 0.0189 30   0.0184    0.112
##  nitrogenio0 - nitrogenio160     0.130 0.0189 30   0.0834    0.177
##  nitrogenio28 - nitrogenio160    0.065 0.0189 30   0.0184    0.112
## 
## Results are averaged over the levels of: genotipo 
## Confidence level used: 0.95 
## Conf-level adjustment: tukey method for comparing a family of 3 estimates

## letras (CLD)
tk_nitrogenio$emmeans %>% multcomp::cld(Letters = letters)

##  nitrogenio emmean     SE df lower.CL upper.CL .group
##  160         0.250 0.0134 30    0.223    0.277  a    
##  28          0.315 0.0134 30    0.288    0.342   b   
##  0           0.380 0.0134 30    0.353    0.407    c  
## 
## Results are averaged over the levels of: genotipo 
## Confidence level used: 0.95 
## P value adjustment: tukey method for comparing a family of 3 estimates 
## significance level used: alpha = 0.05 
## NOTE: If two or more means share the same grouping symbol,
##       then we cannot show them to be different.
##       But we also did not show them to be the same.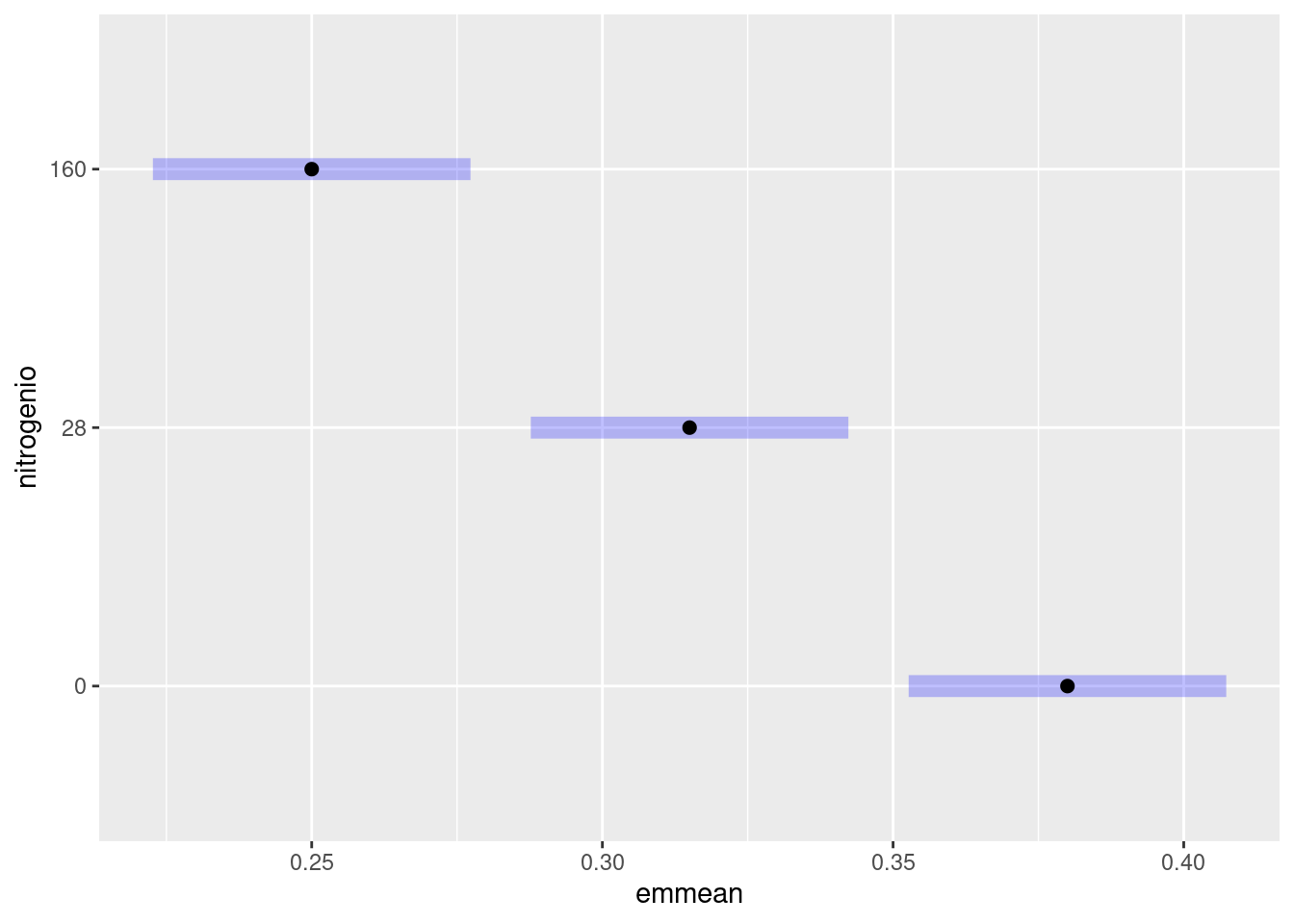

## plot
tk_nitrogenio$emmeans %>% plot()

Teste de comparação de médias para o efeito principal do fator genótipo:

tk_genotipo <- emmeans::emmeans(aov_tomate, ~genotipo, contr = "tukey")

## NOTE: Results may be misleading due to involvement in interactions

## contrastes
tk_genotipo$contrasts

##  contrast           estimate     SE df t.ratio p.value
##  mutante - selvagem   -0.206 0.0154 30 -13.310  <.0001
## 
## Results are averaged over the levels of: nitrogenio

## Intervalo de confiança
tk_genotipo$contrasts %>% confint()

##  contrast           estimate     SE df lower.CL upper.CL
##  mutante - selvagem   -0.206 0.0154 30   -0.237   -0.174
## 
## Results are averaged over the levels of: nitrogenio 
## Confidence level used: 0.95

## letras (CLD)
tk_genotipo$emmeans %>% multcomp::cld(Letters = letters)

##  genotipo emmean     SE df lower.CL upper.CL .group
##  mutante   0.212 0.0109 30    0.190    0.235  a    
##  selvagem  0.418 0.0109 30    0.395    0.440   b   
## 
## Results are averaged over the levels of: nitrogenio 
## Confidence level used: 0.95 
## significance level used: alpha = 0.05 
## NOTE: If two or more means share the same grouping symbol,
##       then we cannot show them to be different.
##       But we also did not show them to be the same.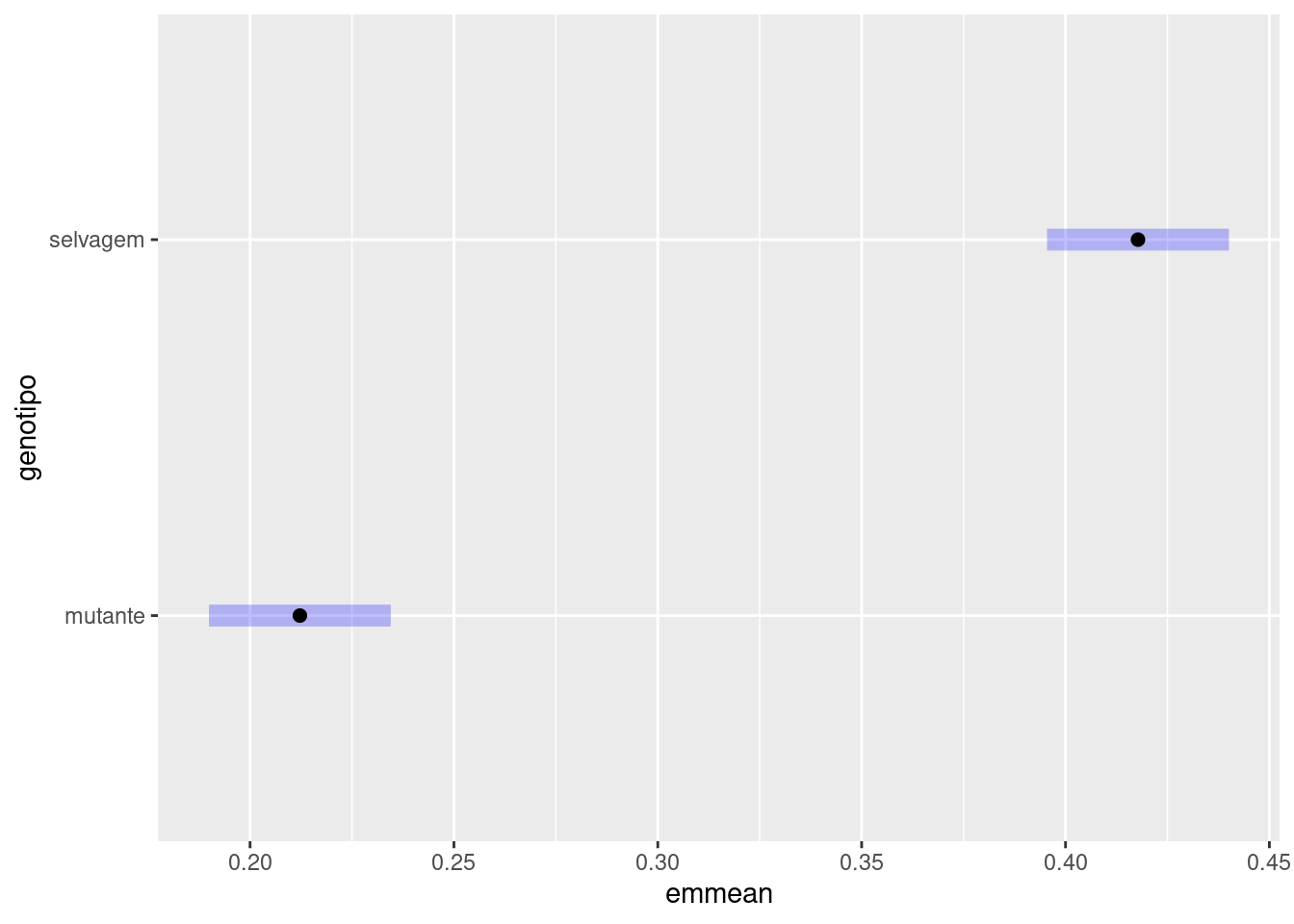

## plot
tk_genotipo$emmeans %>% plot()

Conclusão:

Tomates selvagens com micorrizas tem níveis maiores de fósforo que mutantes sem micorrizas.

O nitrogênio reduz o nível de fosforo nas plantas.

A redução é maior nas plantas selvagens, mas esta interação não é muito grande em termos práticos.

Por último, temos um exemplo em que há uma forte interação que faz os efeitos principais sem sentido. Uma Anova de dois fatores com um efeito de interação forte é frequentemente mais difícil de interpretar.

Exemplo 11.3 (Análise de Variância para dois fatores - interação significativa) Milho com maior conteúdo de aminoácidos pode ser vantajoso na alimentação animal. Nove tratamentos foram arranjados em um fatorial 3x3:

Milho normal e duas variedades alteradas: opaque-2 e floury-2
Doses de proteína na dieta: 20, 16 e 12%

As dietas milho+proteína foram usadas na alimentação de 90 pintinhos machos de 1 dia. A variável resposta é o peso (em gramas) após 21 dias milho.xlsx.

Qual combinação de milho e proteína leva ao maior aumento de peso?

Há três grupos de hipóteses serem testadas:

H₀ : não há interação entre as variedade de milho e a quantidade de proteína.
H₁: há interação entre as variedade de milho e a quantidade de proteína.
H₀: a quantidade de proteína não influencia no peso dos pintinhos.
H₁: a quantidade de proteína influencia no peso dos pintinhos.
H₀: a variedade de milho não influencia no peso dos pintinhos.
H₁: a variedade de milho influencia no peso dos pintinhos.

Análise exploratória:

milho <- readxl::read_excel("data/milho.xlsx") %>%
  mutate(
    variedade = factor(variedade),
    proteina = factor(proteina)
  )


milho %>%
  group_by(variedade, proteina) %>%
  summarise(
    n = n(),
    media = mean(peso),
    desvpad = sd(peso),
    var = var(peso)
  )

## `summarise()` has grouped output by 'variedade'. You can override using the
## `.groups` argument.

## # A tibble: 9 × 6
## # Groups:   variedade [3]
##   variedade proteina     n media desvpad   var
##   <fct>     <fct>    <int> <dbl>   <dbl> <dbl>
## 1 flou      12          10  271.    32.1 1033.
## 2 flou      16          10  434.    49.7 2474.
## 3 flou      20          10  465.    49.2 2416.
## 4 norm      12          10  195.    50.5 2553.
## 5 norm      16          10  389.    48.1 2314.
## 6 norm      20          10  486.    38.7 1496.
## 7 opaq      12          10  264.    26.0  675.
## 8 opaq      16          10  339.    54.4 2959.
## 9 opaq      20          10  438.    61.2 3741.

## Boxplot - Efeito principal fator A
boxplot(peso ~ variedade, data = milho)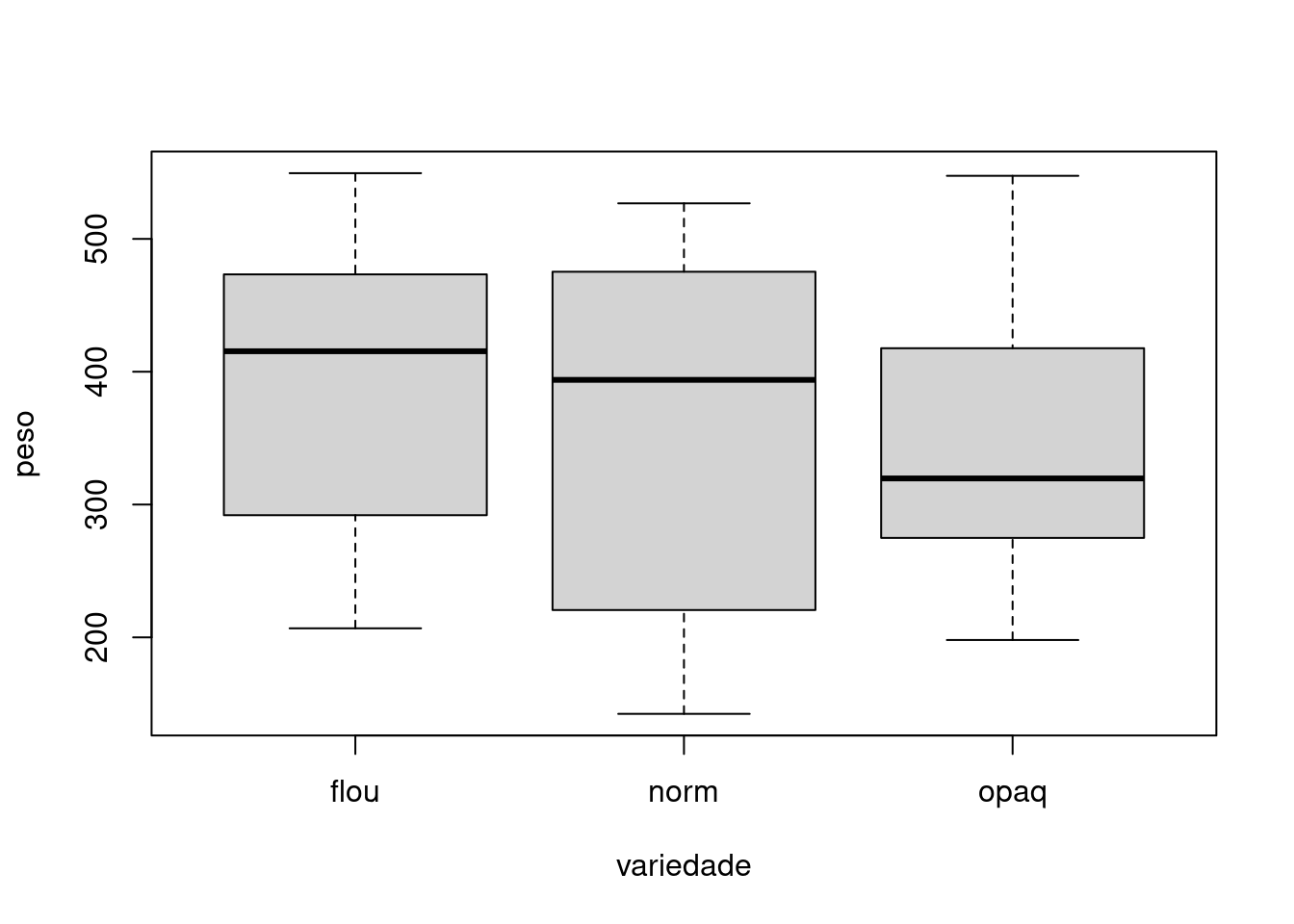

## Boxplot - Efeito principal fator B
boxplot(peso ~ proteina, data = milho)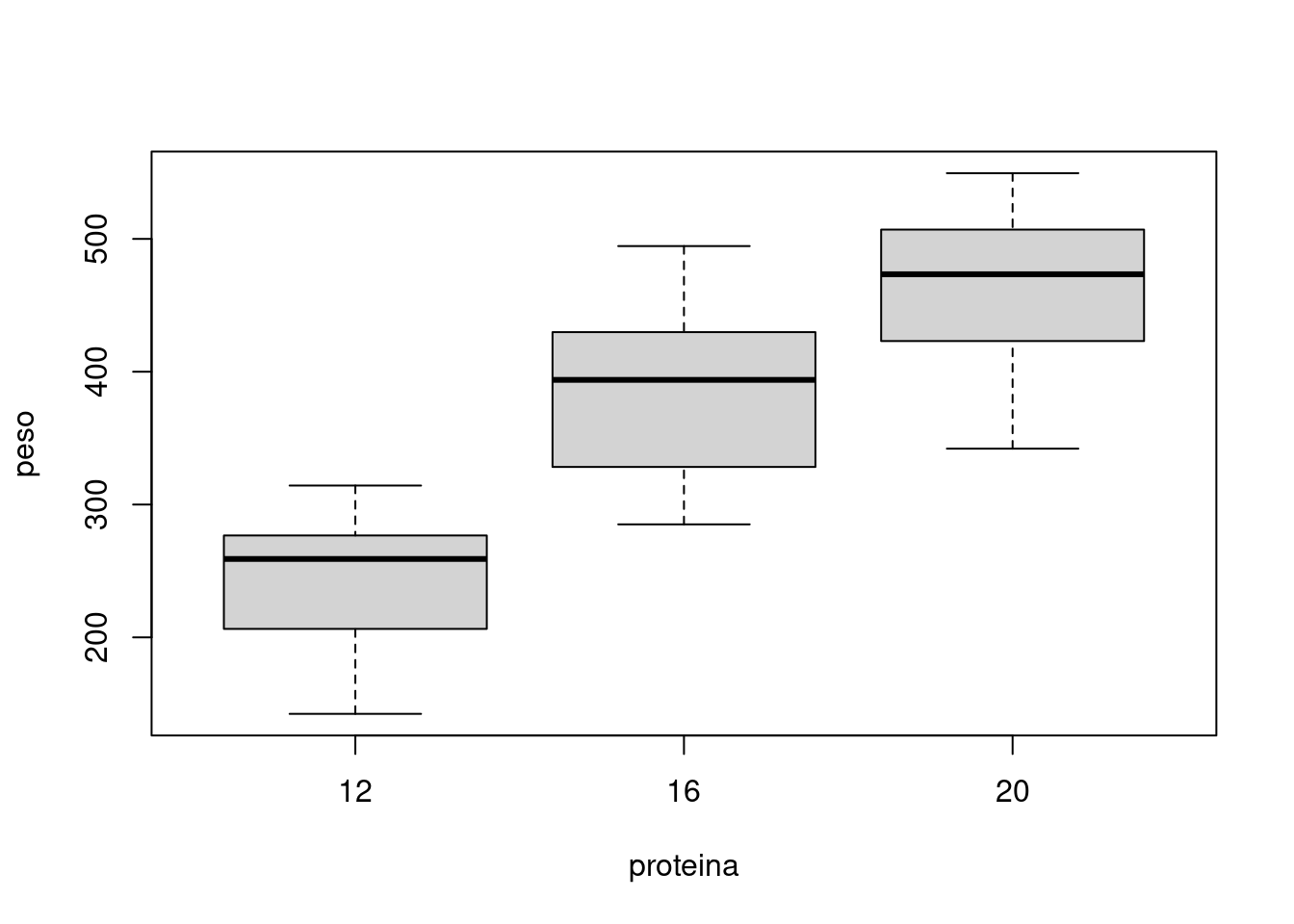

## Boxplot - Interação
boxplot(peso ~ variedade * proteina, data = milho)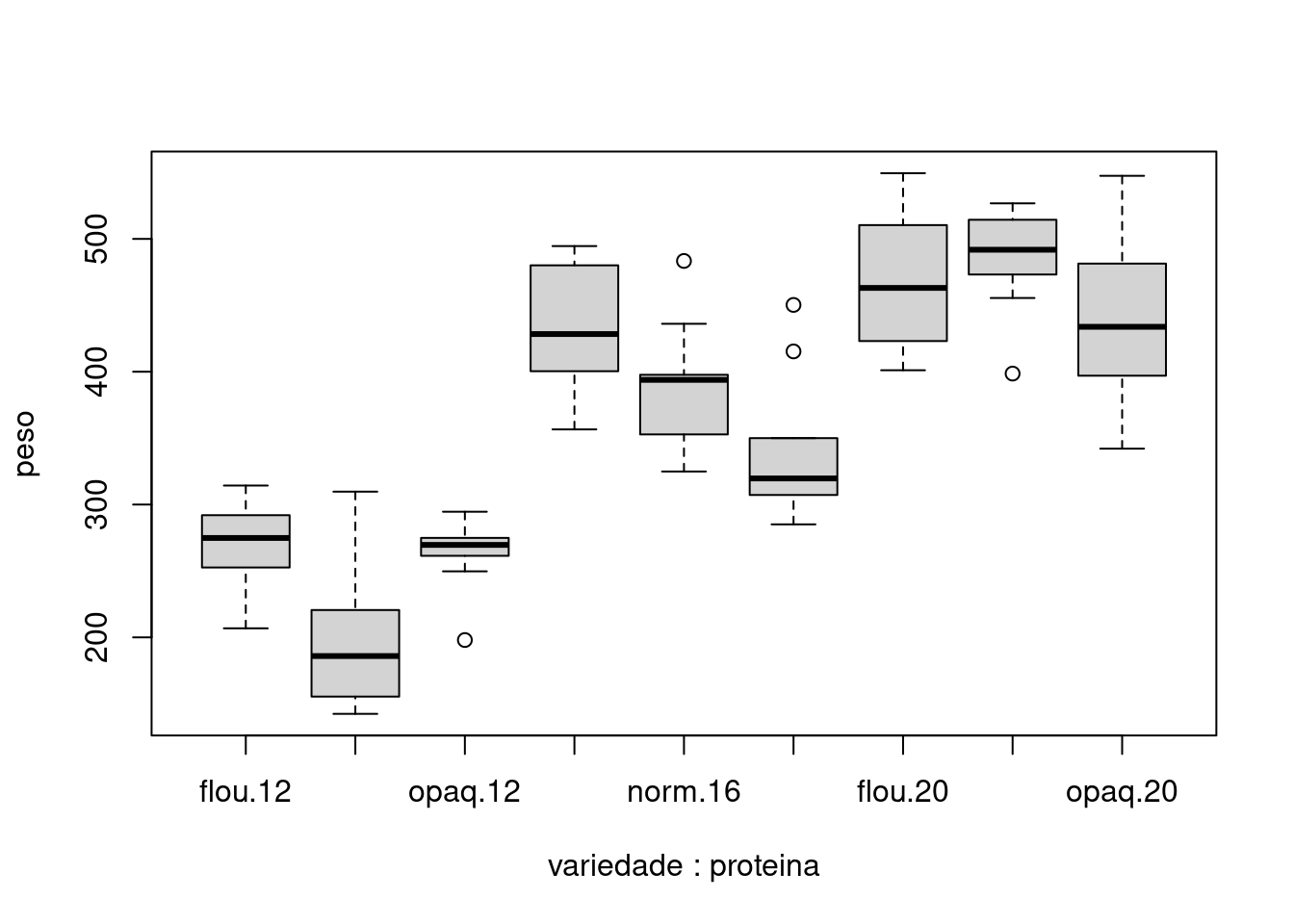

## Gráfico da interação
with(milho, interaction.plot(variedade, proteina, peso))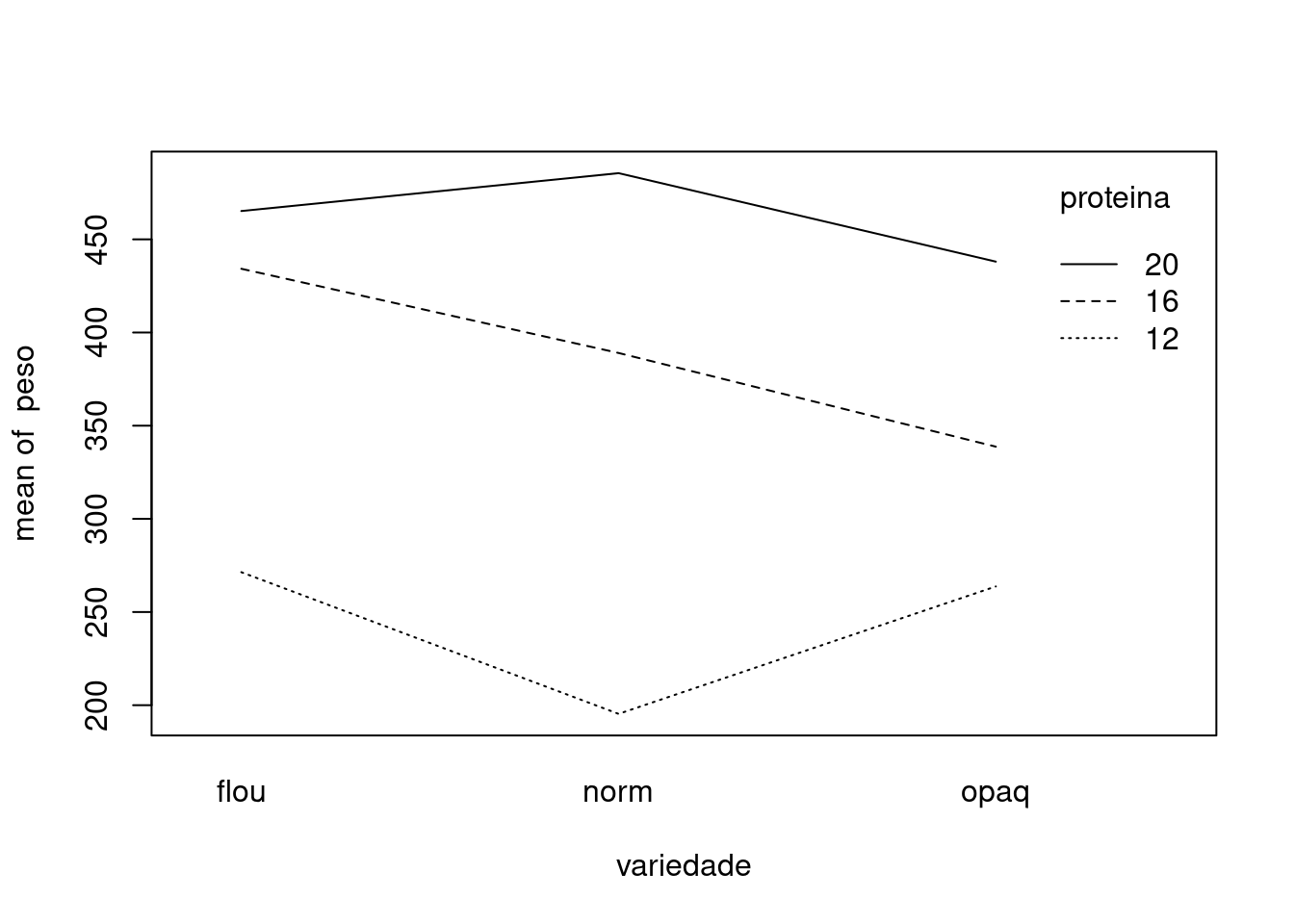

with(milho, interaction.plot(proteina, variedade, peso))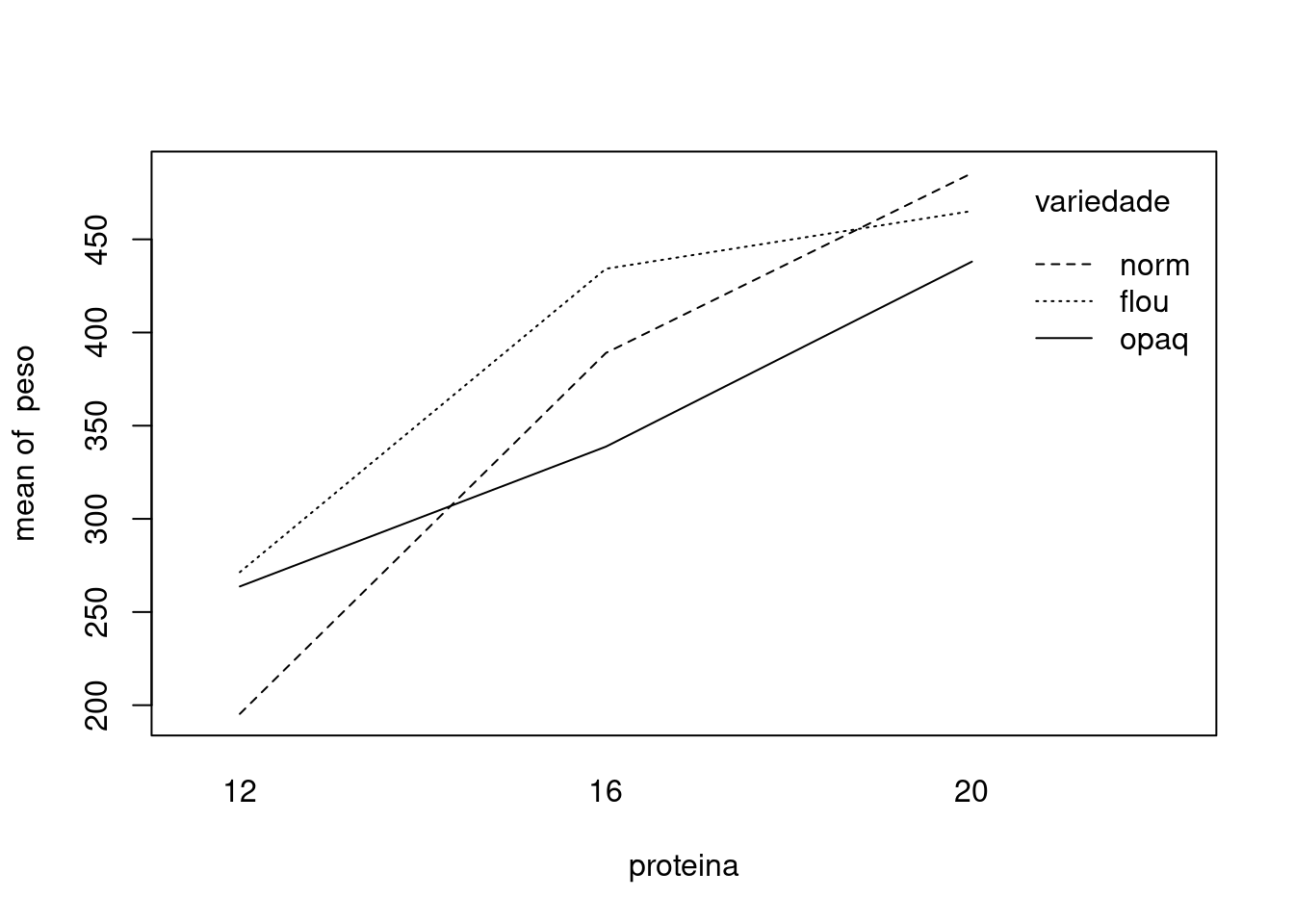

Efetuamos a Análise de Variância para os efeitos principais e para a interação:

aov_milho <- lm(peso ~ variedade * proteina, data = milho)
anova(aov_milho)

## Analysis of Variance Table
## 
## Response: peso
##                    Df Sum Sq Mean Sq  F value    Pr(>F)    
## variedade           2  31137   15568   7.1265   0.00141 ** 
## proteina            2 745621  372810 170.6557 < 2.2e-16 ***
## variedade:proteina  4  60894   15223   6.9686 7.143e-05 ***
## Residuals          81 176951    2185                       
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Verificação dos presupostos da Normalidade e Homogeneidade das Variâncias (análise não mostrada): não há evidência de violação dos pressupostos.

Desdobramento da interação: variedade dentro de cada nível de proteína.

## Desdobramento da interação
phia::testInteractions(aov_milho, fixed="proteina", across="variedade")

## F Test: 
## P-value adjustment method: holm
##           variedade1 variedade2 Df Sum of Sq       F    Pr(>F)    
## 12              7.66     -68.39  2     35065  8.0256 0.0013218 ** 
## 16             95.47      50.28  2     45616 10.4404 0.0002773 ***
## 20             27.16      47.48  2     11350  2.5977 0.0806380 .  
## Residuals                       81    176951                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

## Teste de Tukey para a interação
tk_variedade <- emmeans::emmeans(aov_milho, ~proteina|variedade, contr = "tukey")

## Contrastes
tk_variedade$contrasts

## variedade = flou:
##  contrast                estimate   SE df t.ratio p.value
##  proteina12 - proteina16   -162.8 20.9 81  -7.790  <.0001
##  proteina12 - proteina20   -193.8 20.9 81  -9.273  <.0001
##  proteina16 - proteina20    -31.0 20.9 81  -1.483  0.3046
## 
## variedade = norm:
##  contrast                estimate   SE df t.ratio p.value
##  proteina12 - proteina16   -193.7 20.9 81  -9.266  <.0001
##  proteina12 - proteina20   -290.2 20.9 81 -13.883  <.0001
##  proteina16 - proteina20    -96.5 20.9 81  -4.617  <.0001
## 
## variedade = opaq:
##  contrast                estimate   SE df t.ratio p.value
##  proteina12 - proteina16    -75.0 20.9 81  -3.589  0.0016
##  proteina12 - proteina20   -174.3 20.9 81  -8.340  <.0001
##  proteina16 - proteina20    -99.3 20.9 81  -4.751  <.0001
## 
## P value adjustment: tukey method for comparing a family of 3 estimates

## Intervalo de confiança
tk_variedade$contrasts %>% confint()

## variedade = flou:
##  contrast                estimate   SE df lower.CL upper.CL
##  proteina12 - proteina16   -162.8 20.9 81   -212.7   -112.9
##  proteina12 - proteina20   -193.8 20.9 81   -243.7   -143.9
##  proteina16 - proteina20    -31.0 20.9 81    -80.9     18.9
## 
## variedade = norm:
##  contrast                estimate   SE df lower.CL upper.CL
##  proteina12 - proteina16   -193.7 20.9 81   -243.6   -143.8
##  proteina12 - proteina20   -290.2 20.9 81   -340.1   -240.3
##  proteina16 - proteina20    -96.5 20.9 81   -146.4    -46.6
## 
## variedade = opaq:
##  contrast                estimate   SE df lower.CL upper.CL
##  proteina12 - proteina16    -75.0 20.9 81   -124.9    -25.1
##  proteina12 - proteina20   -174.3 20.9 81   -224.2   -124.4
##  proteina16 - proteina20    -99.3 20.9 81   -149.2    -49.4
## 
## Confidence level used: 0.95 
## Conf-level adjustment: tukey method for comparing a family of 3 estimates

## letras (CLD)
tk_variedade$emmeans %>% multcomp::cld(Letters = letters)

## variedade = flou:
##  proteina emmean   SE df lower.CL upper.CL .group
##  12          271 14.8 81      242      301  a    
##  16          434 14.8 81      405      464   b   
##  20          465 14.8 81      436      495   b   
## 
## variedade = norm:
##  proteina emmean   SE df lower.CL upper.CL .group
##  12          195 14.8 81      166      225  a    
##  16          389 14.8 81      360      418   b   
##  20          486 14.8 81      456      515    c  
## 
## variedade = opaq:
##  proteina emmean   SE df lower.CL upper.CL .group
##  12          264 14.8 81      234      293  a    
##  16          339 14.8 81      309      368   b   
##  20          438 14.8 81      409      467    c  
## 
## Confidence level used: 0.95 
## P value adjustment: tukey method for comparing a family of 3 estimates 
## significance level used: alpha = 0.05 
## NOTE: If two or more means share the same grouping symbol,
##       then we cannot show them to be different.
##       But we also did not show them to be the same.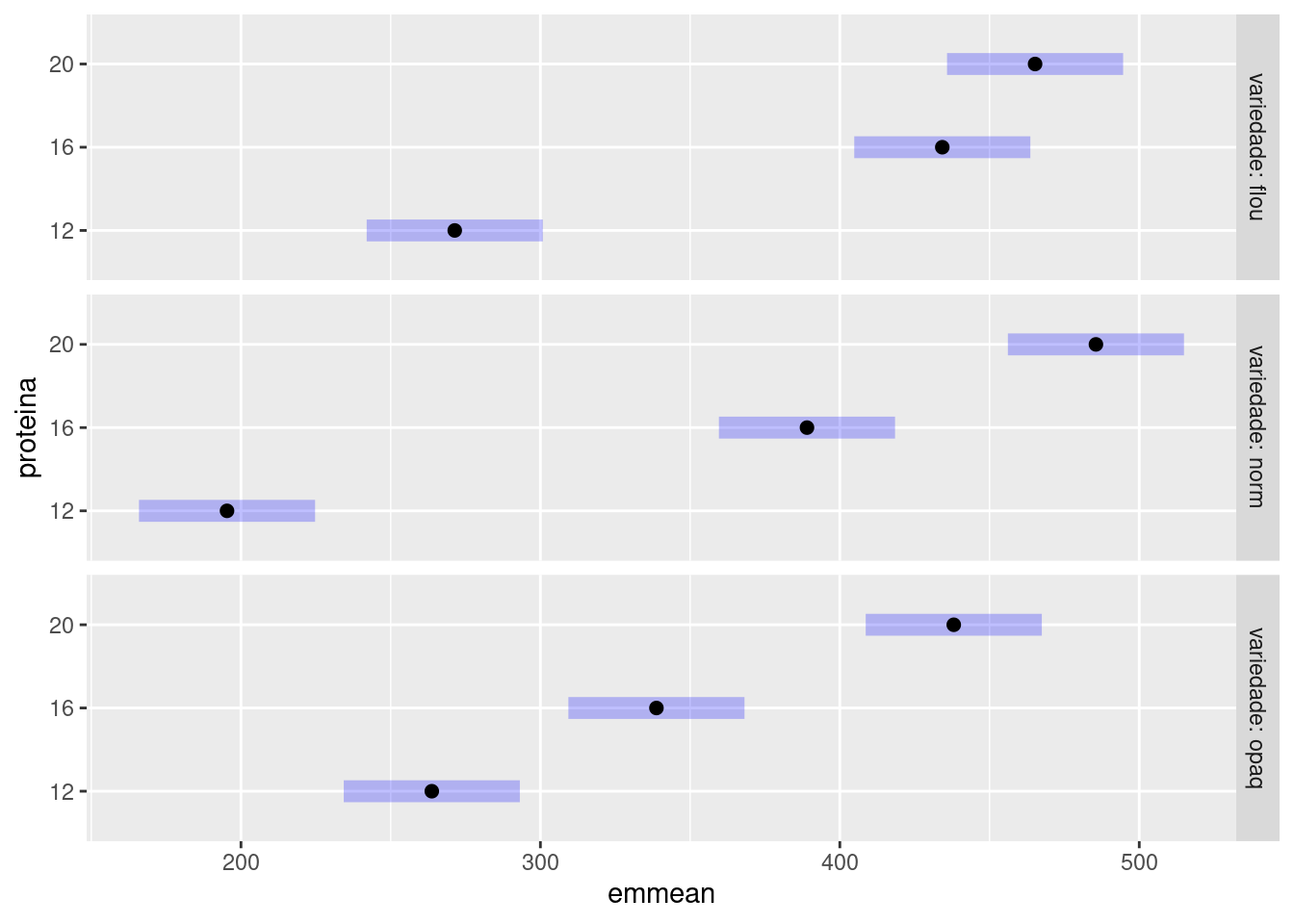

## plot
tk_variedade$emmeans %>% plot()

Desdobramento da interação: proteína dentro de cada nível de variedade.

## Desdobramento da interação
phia::testInteractions(aov_milho, fixed="variedade", across="proteina")

## F Test: 
## P-value adjustment method: holm
##           proteina1 proteina2 Df Sum of Sq      F    Pr(>F)    
## flou        -193.82    -30.99  2    216801 49.621 1.708e-14 ***
## norm        -290.19    -96.50  2    436794 99.972 < 2.2e-16 ***
## opaq        -174.32    -99.30  2    152920 35.000 1.109e-11 ***
## Residuals                     81    176951                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

## Teste de Tukey para a interação
tk_proteina <- emmeans::emmeans(aov_milho, ~variedade|proteina, contr = "tukey")

## Contrastes
tk_proteina$contrasts

## proteina = 12:
##  contrast    estimate   SE df t.ratio p.value
##  flou - norm    76.05 20.9 81   3.638  0.0014
##  flou - opaq     7.66 20.9 81   0.366  0.9287
##  norm - opaq   -68.39 20.9 81  -3.272  0.0044
## 
## proteina = 16:
##  contrast    estimate   SE df t.ratio p.value
##  flou - norm    45.19 20.9 81   2.162  0.0840
##  flou - opaq    95.47 20.9 81   4.567  0.0001
##  norm - opaq    50.28 20.9 81   2.405  0.0479
## 
## proteina = 20:
##  contrast    estimate   SE df t.ratio p.value
##  flou - norm   -20.32 20.9 81  -0.972  0.5965
##  flou - opaq    27.16 20.9 81   1.299  0.3997
##  norm - opaq    47.48 20.9 81   2.271  0.0657
## 
## P value adjustment: tukey method for comparing a family of 3 estimates

## Intervalo de confiança
tk_proteina$contrasts %>% confint()

## proteina = 12:
##  contrast    estimate   SE df lower.CL upper.CL
##  flou - norm    76.05 20.9 81   26.144    126.0
##  flou - opaq     7.66 20.9 81  -42.246     57.6
##  norm - opaq   -68.39 20.9 81 -118.296    -18.5
## 
## proteina = 16:
##  contrast    estimate   SE df lower.CL upper.CL
##  flou - norm    45.19 20.9 81   -4.716     95.1
##  flou - opaq    95.47 20.9 81   45.564    145.4
##  norm - opaq    50.28 20.9 81    0.374    100.2
## 
## proteina = 20:
##  contrast    estimate   SE df lower.CL upper.CL
##  flou - norm   -20.32 20.9 81  -70.226     29.6
##  flou - opaq    27.16 20.9 81  -22.746     77.1
##  norm - opaq    47.48 20.9 81   -2.426     97.4
## 
## Confidence level used: 0.95 
## Conf-level adjustment: tukey method for comparing a family of 3 estimates

## letras (CLD)
tk_proteina$emmeans %>% multcomp::cld(Letters = letters)

## proteina = 12:
##  variedade emmean   SE df lower.CL upper.CL .group
##  norm         195 14.8 81      166      225  a    
##  opaq         264 14.8 81      234      293   b   
##  flou         271 14.8 81      242      301   b   
## 
## proteina = 16:
##  variedade emmean   SE df lower.CL upper.CL .group
##  opaq         339 14.8 81      309      368  a    
##  norm         389 14.8 81      360      418   b   
##  flou         434 14.8 81      405      464   b   
## 
## proteina = 20:
##  variedade emmean   SE df lower.CL upper.CL .group
##  opaq         438 14.8 81      409      467  a    
##  flou         465 14.8 81      436      495  a    
##  norm         486 14.8 81      456      515  a    
## 
## Confidence level used: 0.95 
## P value adjustment: tukey method for comparing a family of 3 estimates 
## significance level used: alpha = 0.05 
## NOTE: If two or more means share the same grouping symbol,
##       then we cannot show them to be different.
##       But we also did not show them to be the same.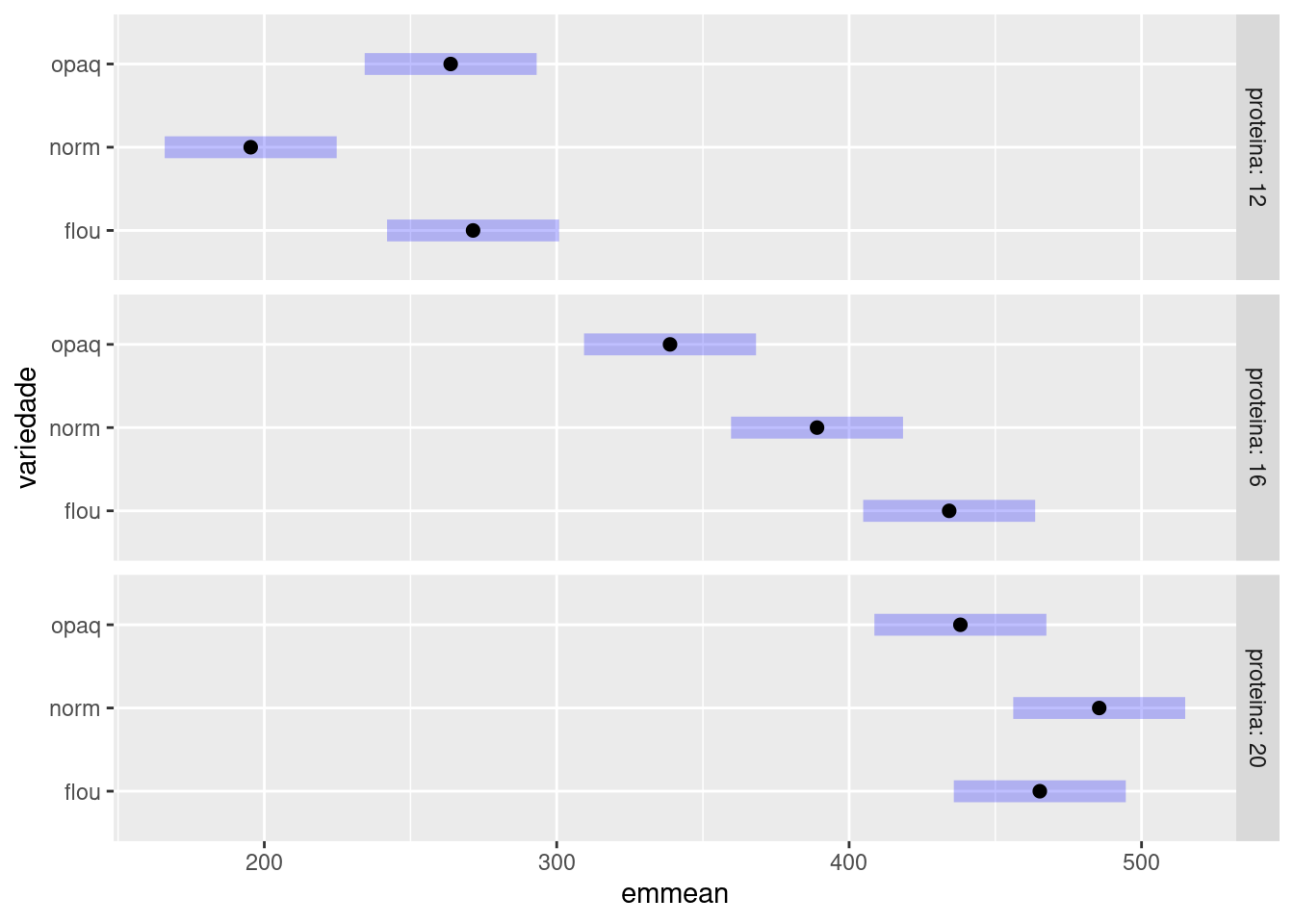

## plot
tk_proteina$emmeans %>% plot()

Há um efeito importante da interação:

O milho normal é o pior para 12% de proteína e o melhor para 20%. Floury é o melhor para 12% e 16% de proteína. Opaque é sempre inferior ao Floury, mas melhor que o normal somente para 12% de proteína.

Apesar de haver um efeito principal para variedade e proteína, estes são menos importantes devido a interação.

Conclusão:

Maior dose de proteína ajuda a acelerar o ganho de peso.
Os três tipos de milho não diferem quando a dieta tem 20% de proteína.
Floury é melhor quando a dose de proteína é de 16% e 20%.

10 Análise de Variância

12 Correlação e Regressão