
Capítulo 6 Estatística Básica
Neste capítulo, iremos estudar alguns itens que podem ser compreendidos como a base das análises estatísticas, pois são usados transversalmente em muitos outros assuntos tratados posteriormente.
Para facilitar o entendimento, alguns dos próximos exemplos (deste e dos próximos capítulos) utilizarão os dados obtidos em uma população conforme descrito a seguir.
Considere uma população com 150 árvores pertencente a um reflorestamento de Mogno Africano. O DAP destas árvores foi medido aos 5 anos após o plantio e os dados são mostrados na tabela abaixo:
| 14.80 | 12.26 | 13.77 | 14.28 | 15.01 | 12.83 | 14.98 | 14.77 | 12.88 | 13.77 |
| 11.59 | 14.44 | 12.52 | 14.12 | 10.44 | 16.19 | 13.59 | 10.92 | 11.42 | 15.64 |
| 13.54 | 10.87 | 12.80 | 16.48 | 14.78 | 15.31 | 16.83 | 14.69 | 12.63 | 13.09 |
| 12.79 | 11.78 | 10.94 | 13.77 | 13.48 | 10.60 | 13.00 | 13.78 | 12.38 | 7.92 |
| 15.59 | 11.02 | 11.85 | 13.50 | 14.97 | 13.49 | 13.80 | 15.21 | 14.14 | 12.22 |
| 11.46 | 14.42 | 13.32 | 11.39 | 14.55 | 10.04 | 15.13 | 11.09 | 12.05 | 10.98 |
| 11.96 | 10.78 | 11.49 | 11.80 | 10.87 | 12.91 | 12.48 | 10.34 | 12.79 | 11.73 |
| 10.84 | 11.69 | 13.78 | 11.21 | 15.16 | 11.79 | 11.96 | 14.34 | 13.63 | 12.86 |
| 12.09 | 10.36 | 12.59 | 16.02 | 12.00 | 14.24 | 13.70 | 12.09 | 11.84 | 9.86 |
| 12.75 | 11.05 | 15.00 | 10.64 | 12.89 | 11.48 | 13.89 | 11.84 | 11.95 | 11.99 |
| 12.29 | 15.57 | 12.50 | 15.84 | 8.78 | 11.29 | 10.16 | 11.65 | 15.60 | 14.07 |
| 11.61 | 13.88 | 13.47 | 16.68 | 12.91 | 14.52 | 15.55 | 10.00 | 13.76 | 12.22 |
| 14.15 | 14.57 | 16.71 | 13.46 | 12.10 | 11.36 | 12.60 | 13.33 | 16.45 | 9.80 |
| 14.87 | 15.46 | 15.38 | 10.96 | 13.91 | 12.64 | 14.39 | 11.69 | 11.05 | 11.55 |
| 10.74 | 14.46 | 11.16 | 12.49 | 12.85 | 14.55 | 11.98 | 14.24 | 14.87 | 11.13 |
Os dados também podem ser acessados no arquivo dap.csv.
6.1 Medidas de centro
Média
A média aritmética é a medida de centro mais comum. É o resultado da soma de um conjunto de números dividido pelo número total de elementos nesse conjunto.
Mediana
É o ponto do meio de uma distribuição, o número em relação ao qual metade das observações é menor, e metade, maior.
6.2 Medidas de dispersão
As medidas de dispersão descrevem a variabilidade dos dados.
6.2.1 Quartil
Os quartis delimitam a metade central.
- O primeiro quartil (Q1) cai em um quarto do caminho da lista.
- O terceiro quartil (Q3) cai em três quartos do caminho na lista.
- A Amplitude interquartil (AIQ) é a diferença entre o 3º e 1º quartil
Conhecendo os quartis, podemos descrever uma distribuição com um Resumo de cinco números. São eles:
- menor observação
- primeiro quartil
- mediana
- terceiro quartil
- maior observação
6.3 Descrição de uma distribuição
Qualquer conjunto de dados pode (e deve) ser descrito por meio dos resumos numéricos juntamente com a análise gráfica.
Essa descrição visa também verificar a assimetria dos dados e a presença de valores discrepantes.
Exemplo 6.4 (Descrição de uma distribuição simétrica) Considere o conjunto de dados dap.csv.
Descreva esta distribuição com o uso de gráficos e resumos numéricos.
# Histograma
hist(dap)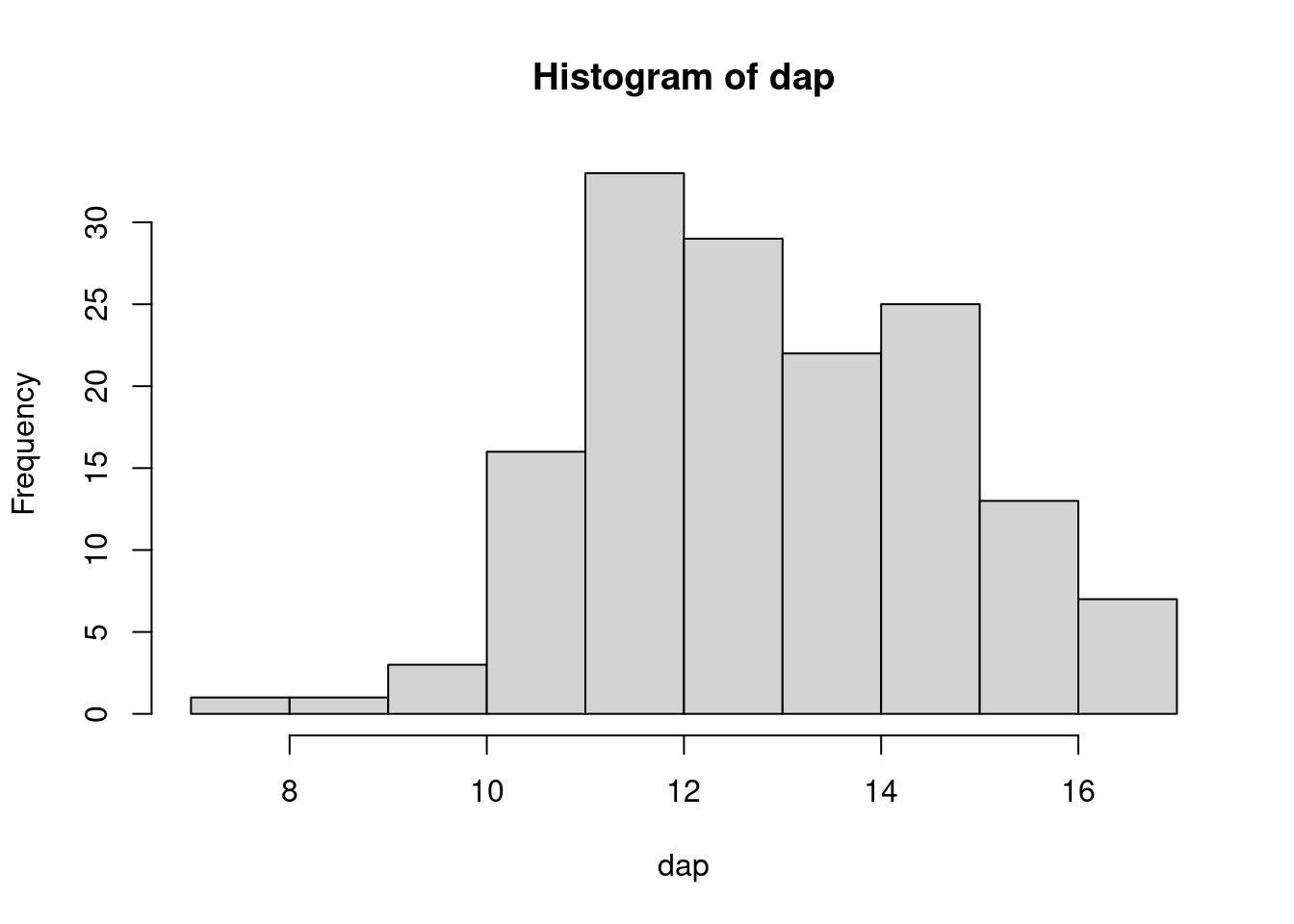
# Diagrama de ramo e folhas
stem(dap)##
## The decimal point is at the |
##
## 7 | 9
## 8 |
## 8 | 8
## 9 |
## 9 | 89
## 10 | 002344
## 10 | 667889999
## 11 | 0001111223444
## 11 | 5556667777888889
## 12 | 000000111122334
## 12 | 5555666688888999999
## 13 | 0133
## 13 | 5555556678888888999
## 14 | 11122233444
## 14 | 55666788899
## 15 | 000012234
## 15 | 5666668
## 16 | 02
## 16 | 55778
# Box-plot
boxplot(dap)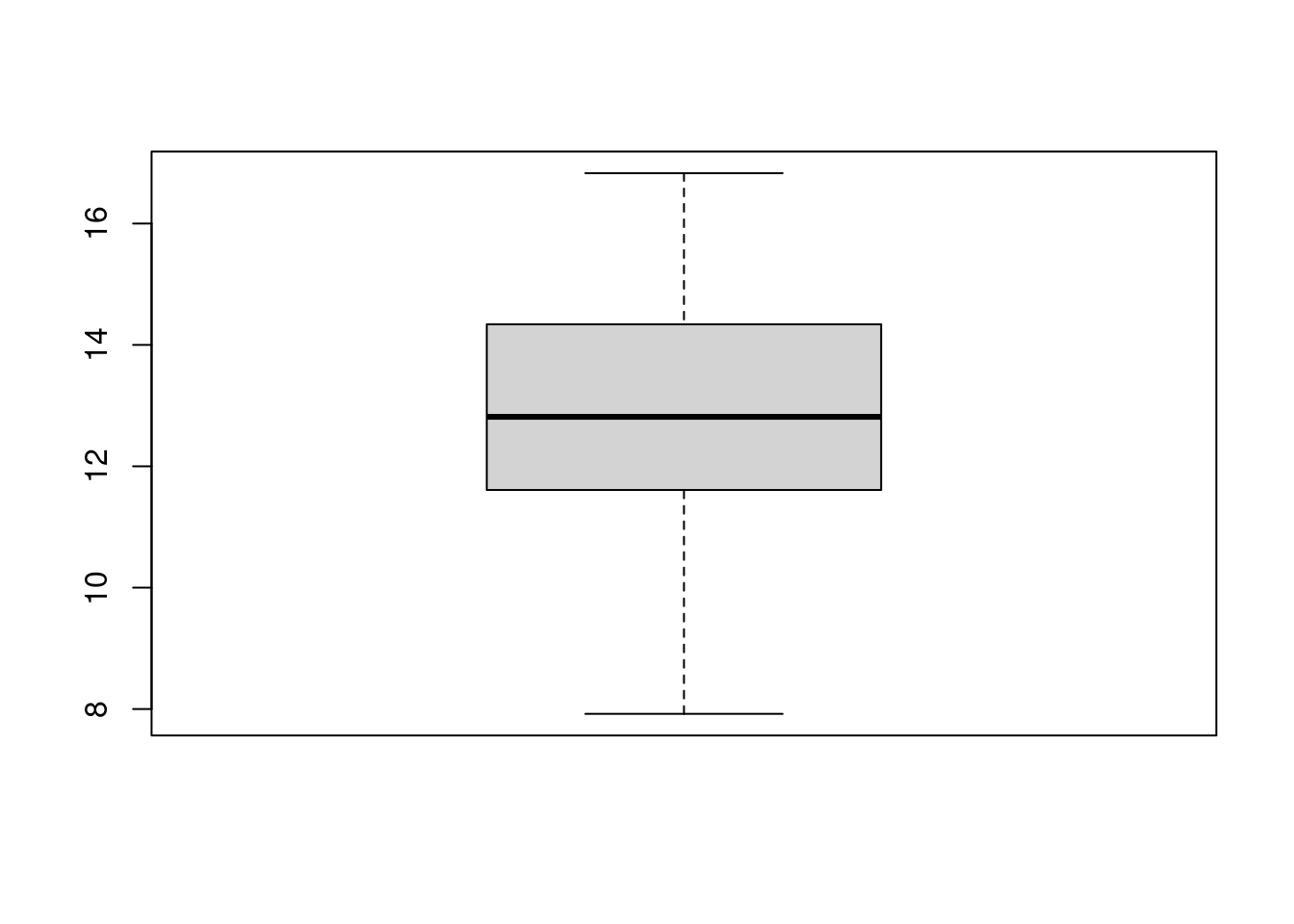
Esta é uma distribuição simétrica e que não possui valores atípicos.
O DAP média da população é de 12.95 cm com desvio-padrão de 1.78.
Vejamos outro exemplo com uma distribuição bastante diferente
Exemplo 6.5 (Descrição de uma distribuição assimétrica) Considere os dados do tempo de sobrevivência de porquinhos-da-índia após terem recebido uma injeção de bactéria infecciosa em um experimento médico.
Os dados podem ser encontrados no arquivo porquinho.xlsx
# Histograma
hist(porq)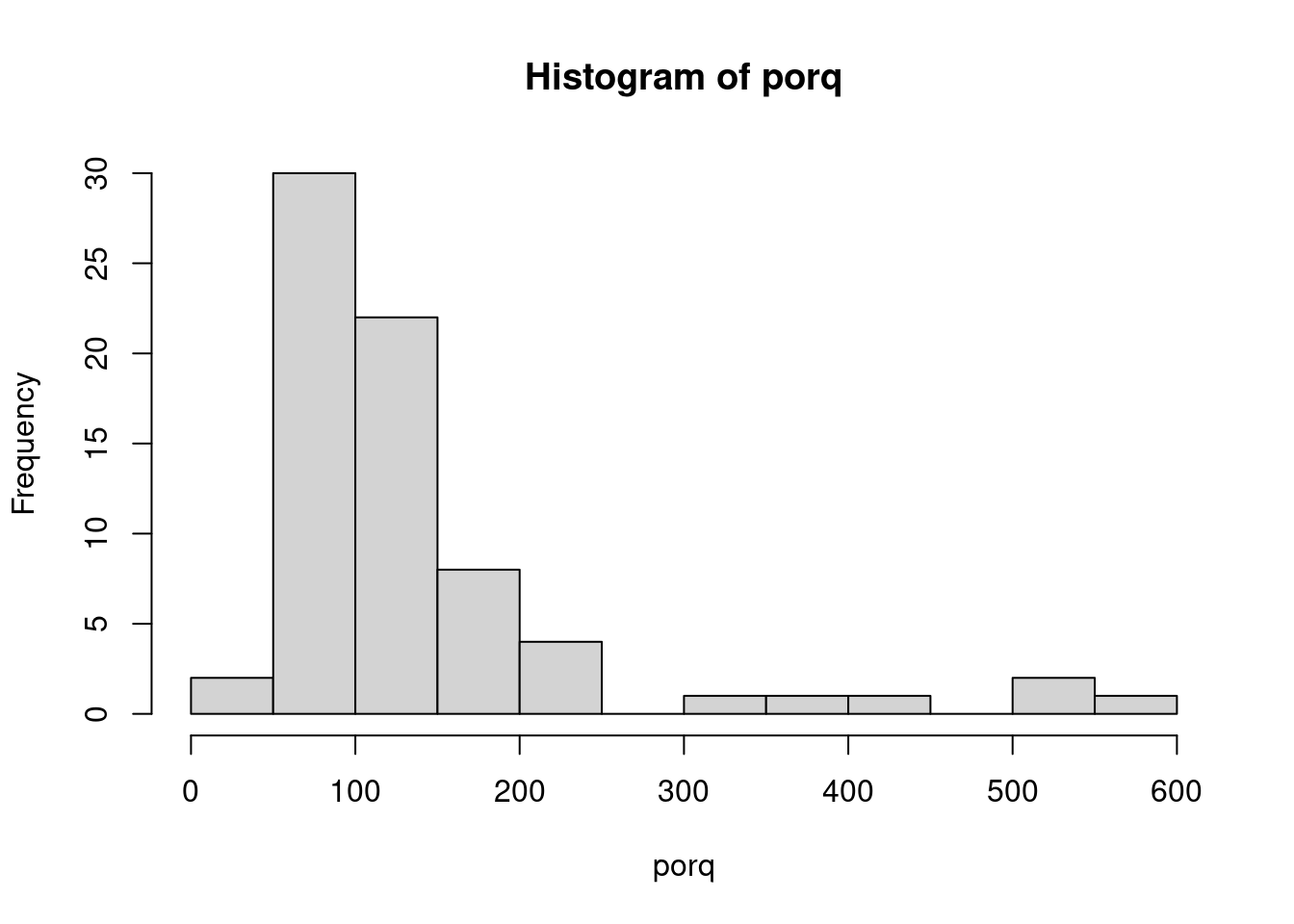
# Diagrama de ramo e folhas
stem(porq)##
## The decimal point is 2 digit(s) to the right of the |
##
## 0 | 455666677778888888888999999
## 1 | 0000000000011111222334444556678889
## 2 | 01145
## 3 | 38
## 4 | 0
## 5 | 12
## 6 | 0
# Box-plot
boxplot(porq)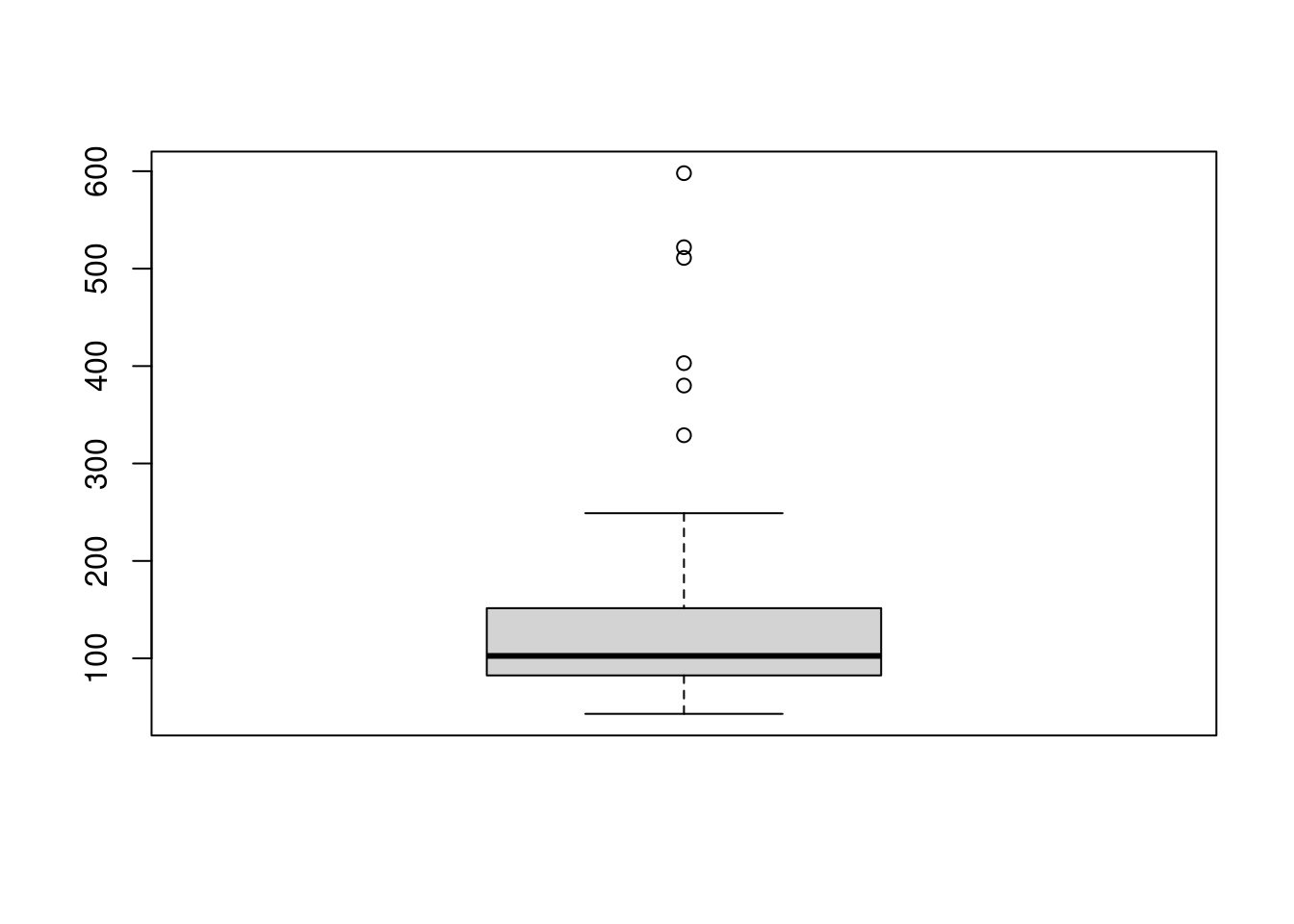
A distribuição é assimétrica á direita. A mediana da distribuição é 102.5.
O resumo de cinco números é 43, 82.75, 102.5, 149.25, 598
Metade dos porquinhos-da-índia morrem dentro dos primeiros 102 dias. Quase todos não sobrevivem até 149 dias.
No entanto, alguns poucos animais sobrevivem mais, de modo que o gráfico se estende mais para a direita do pico, até o valor mais alto de 598 dias.
Tempos de sobrevivência, seja de máquinas sob esforço ou de pacientes depois de um tratamento, em geral, são assimétricos à direita.
Muitas vezes, uma distribuição pode apresentar dois (ou mais) picos. A existência de mais de um pico sugere que indívíduos de vários tipos estão misturados no conjunto de dados.
Exemplo 6.6 (Descrição de uma distribuição bimodal) Considere o conjunto de dados peixe.csv que contém o comprimento (em cm) de vários peixes apanhados em um rio.
# Histograma
hist(peixe)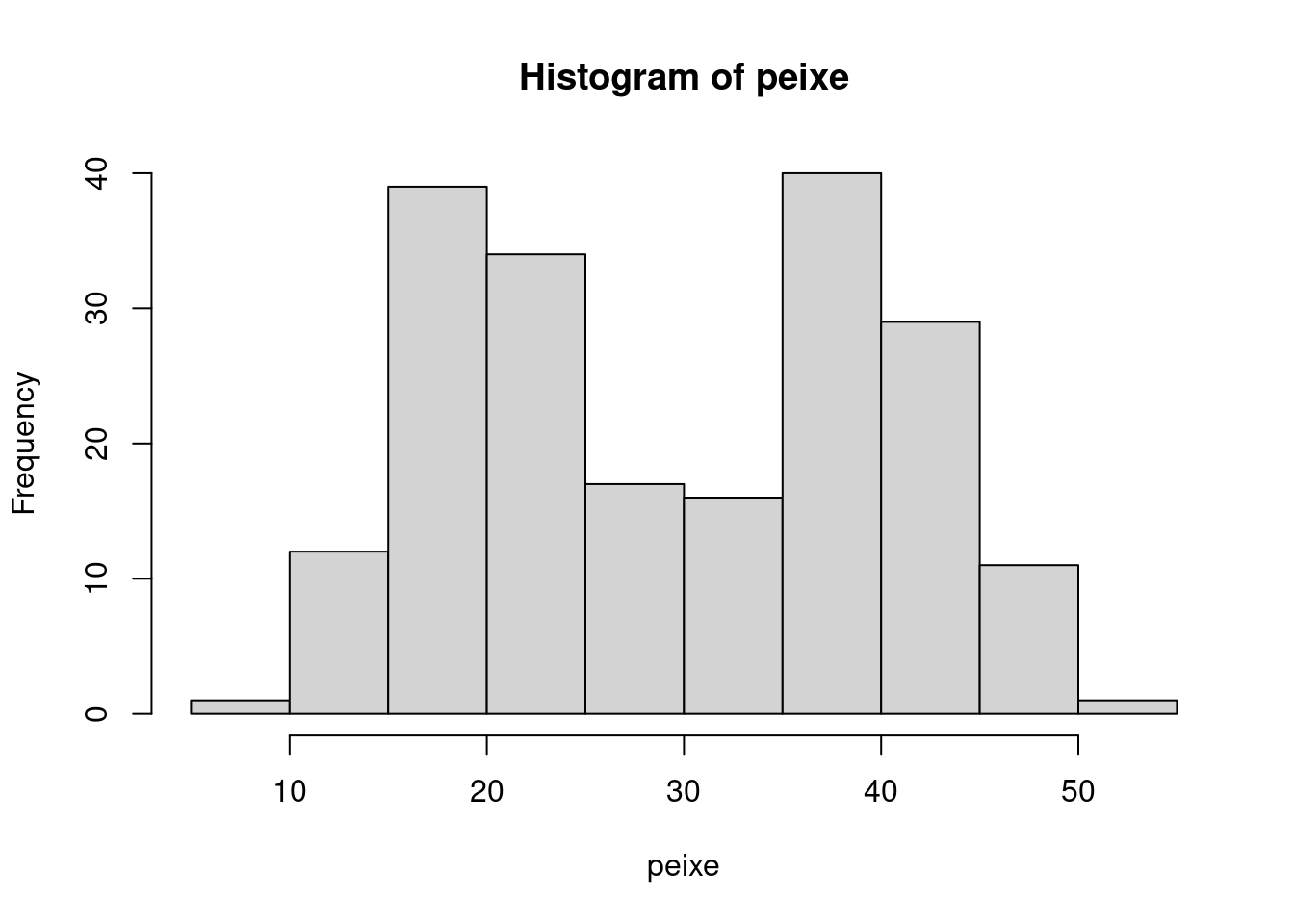
# Diagrama de ramo e folhas
stem(peixe)##
## The decimal point is at the |
##
## 8 | 5
## 10 |
## 12 | 646
## 14 | 013467789114579
## 16 | 0122557900144577
## 18 | 1277780145566788
## 20 | 0822222458999
## 22 | 022389125668999
## 24 | 4579900348
## 26 | 02456135
## 28 | 072356
## 30 | 15
## 32 | 012591234
## 34 | 336801236
## 36 | 000344678901145556679
## 38 | 00159001335577
## 40 | 025682556899
## 42 | 03555578012356
## 44 | 02475569
## 46 | 456815
## 48 | 6
## 50 | 2Esta é uma distribuição bimodal, ou seja, tem dois picos, que representam peixes menores e maiores.
A média da distribuição é 29.67 cm. Veja que este valor pouco representa a distribuição, pois a média está no “vale” entre os picos, ou seja, uma região que contém poucos valores.
Os dois picos podem refletir um dimorfismo sexual (machos maiores que fêmeas ou vice-versa) ou a presença de duas raças de peixes no rio.
A descrição separada das duas distribuições pode ser bem mais útil. Veja o arquivo peixe2.csv
# Histograma para peixes machos
hist(peixe2$m)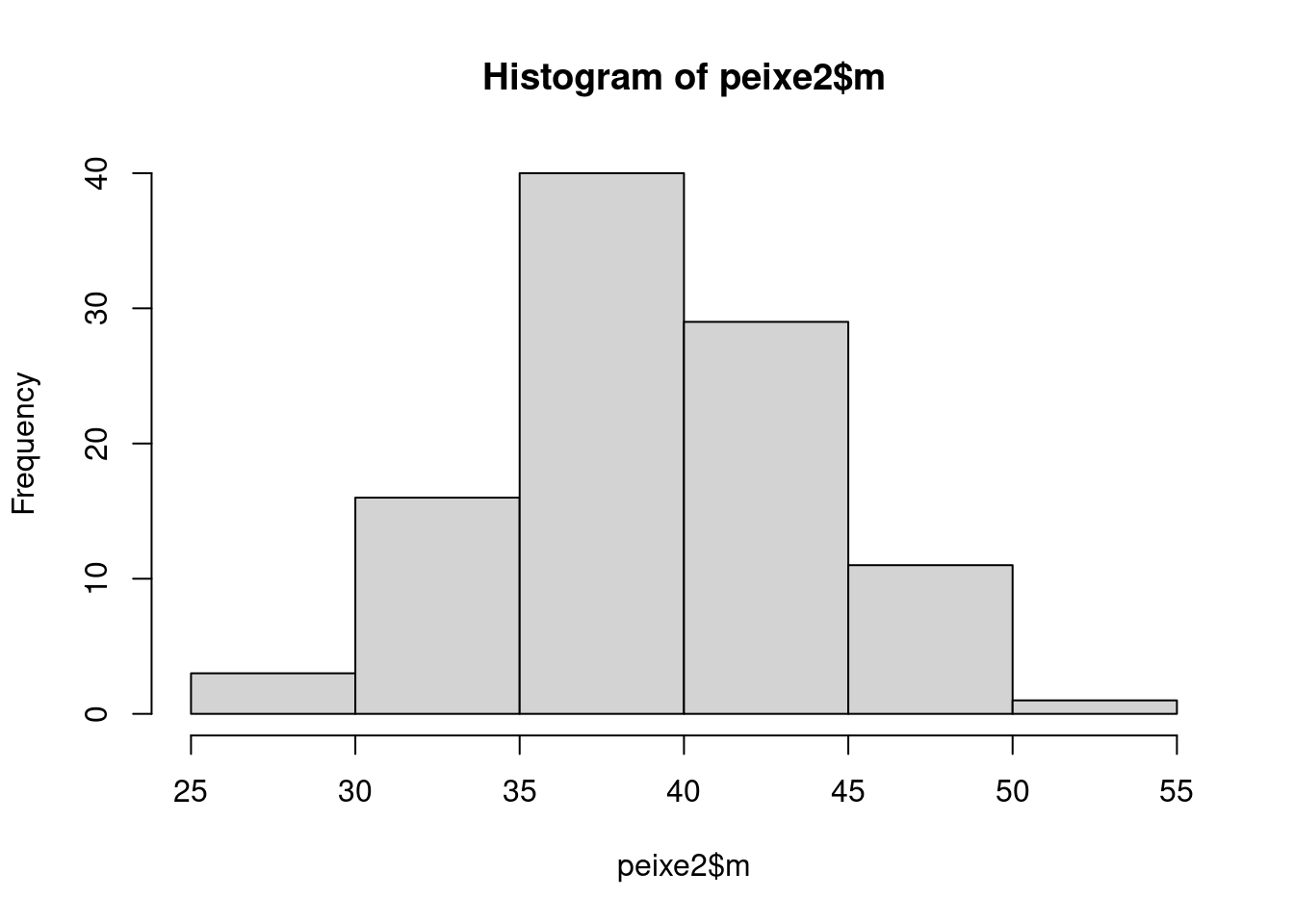
# Histograma para peixes fêmeas
hist(peixe2$f)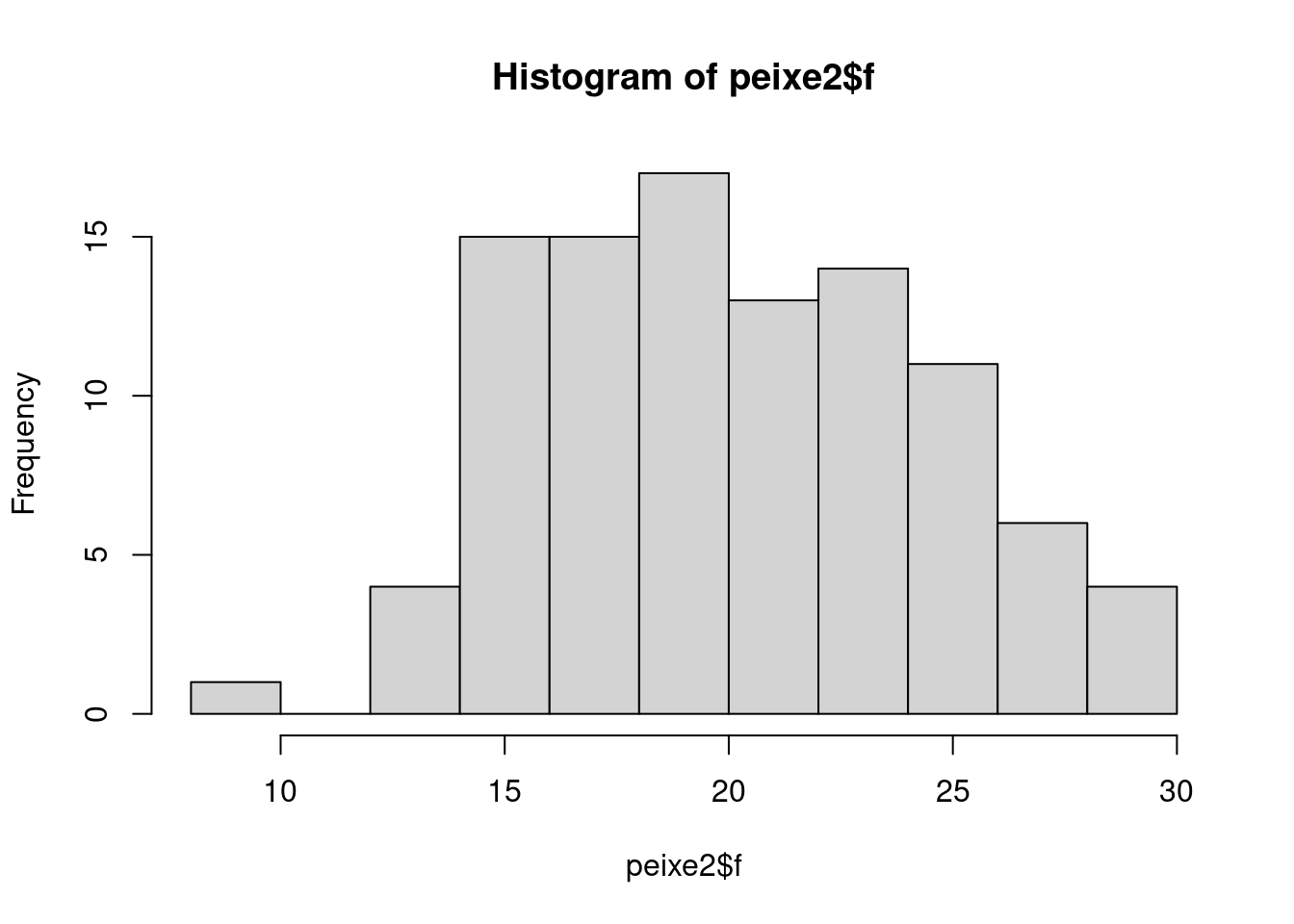
A média do tamanho dos peixes machos é 39.1 cm e dos peixes fêmeas é 20.3 cm.
Por fim, pode haver nas distribuições um ou alguns poucos valores discrepantes, ou seja, valores que diferem consideravelmente dos demais. Muito frequentemente, também são chamados de outliers.
Exemplo 6.7 (Descrição de uma distribuição com valores discrepantes) Considere os dados de produção de morango (em g/planta) contidos no arquivo morango.csv.
# Histograma
hist(morango)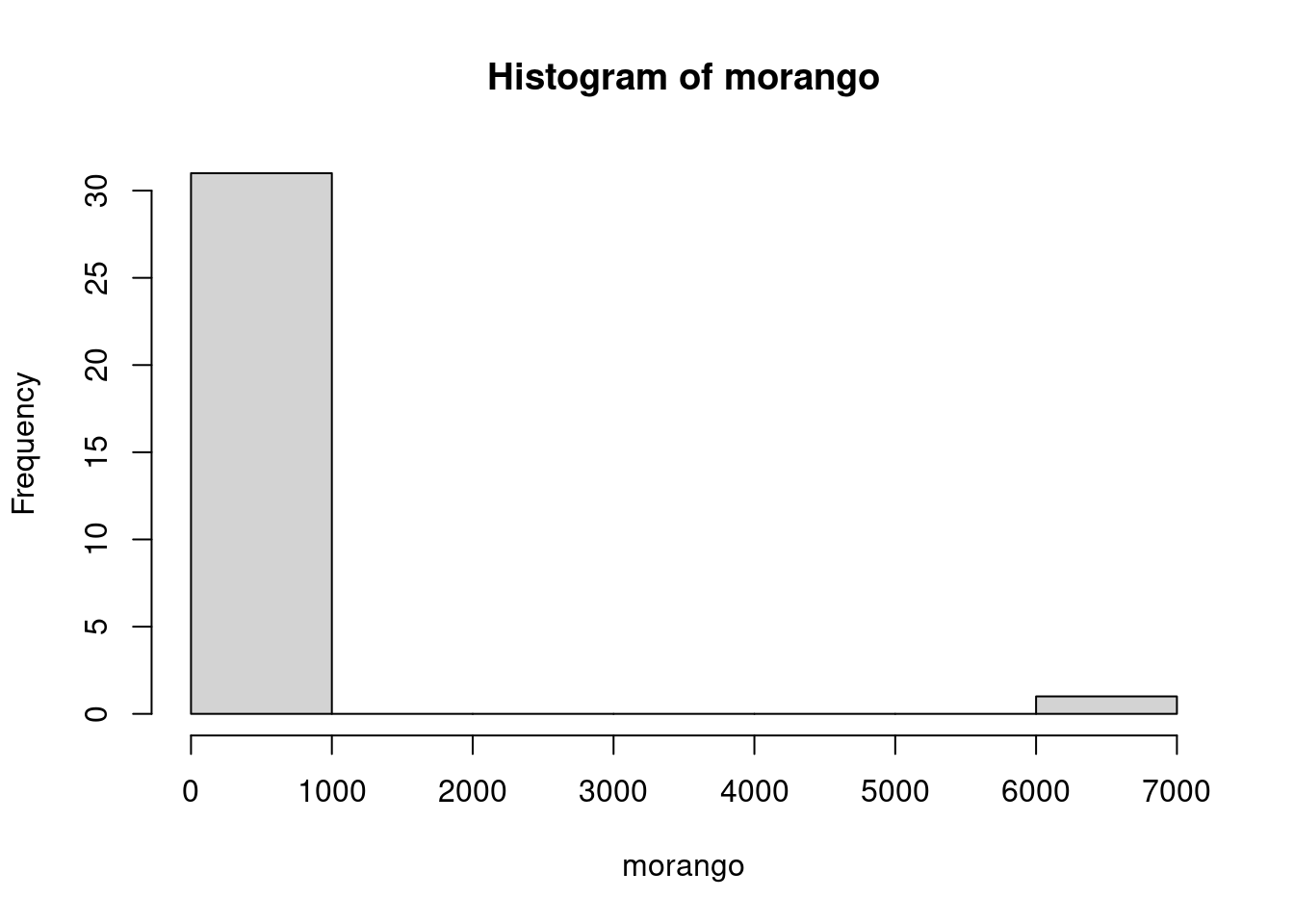
# Diagrama de ramo e folhas
stem(morango)##
## The decimal point is 3 digit(s) to the right of the |
##
## 0 | 6666666666666777777778888888888
## 1 |
## 2 |
## 3 |
## 4 |
## 5 |
## 6 | 9
# Box-plot
boxplot(morango)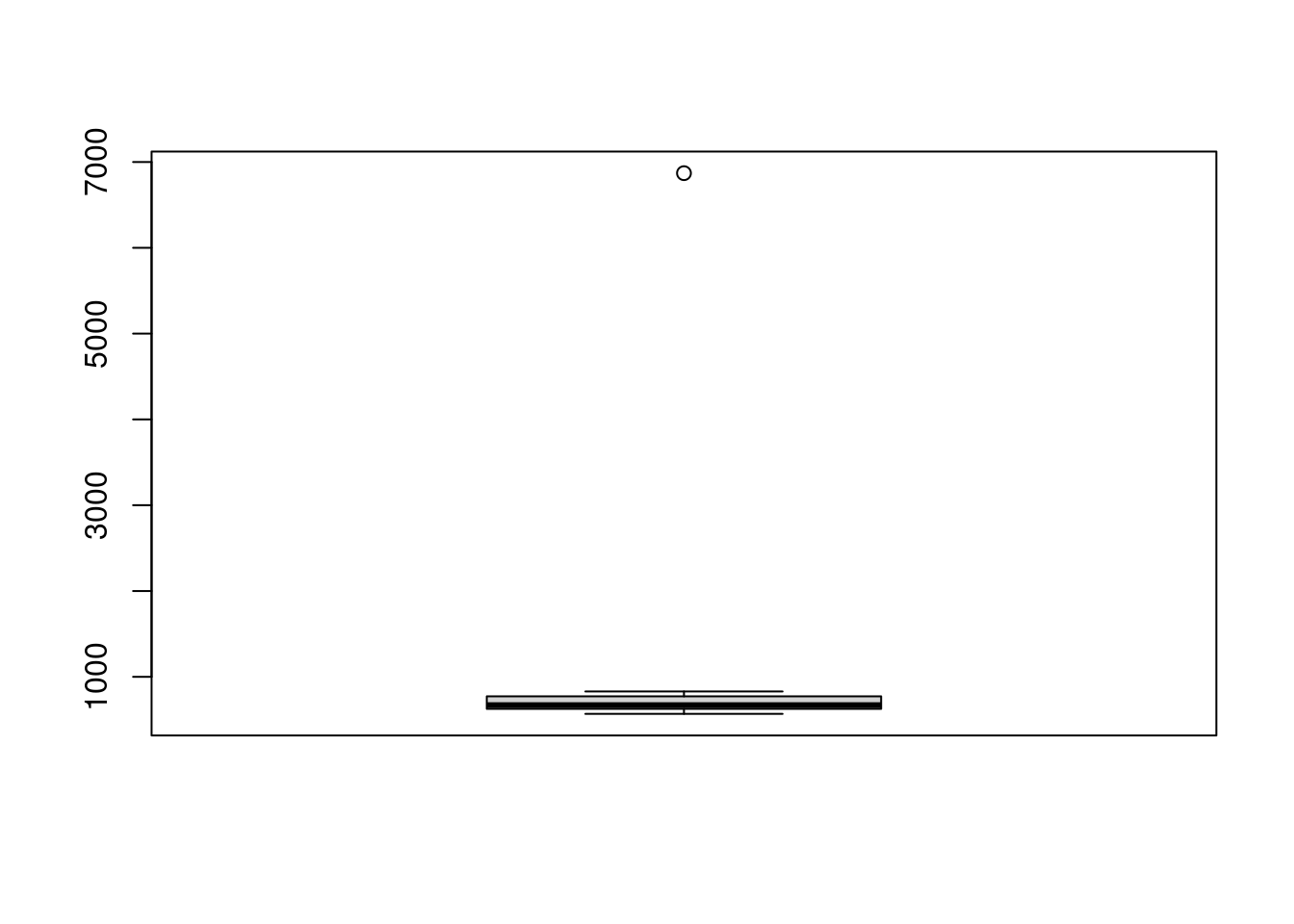
Esta distribuição apresenta claramente um valor discrepante: 6870 g na posição 10 do conjunto de dados.
A média da distribuição é 883.8 g e a mediana é 670 g.
O desvio-padrão é 1095.4 e o resumo de cinco números é 568, 628.25, 670, 772.25, 6870.
Ao se excluir este valor discrepante (outlier), veja como fica a distribuição.
morango2 <- morango
morango2[10] <- NA
# Histograma
hist(morango2)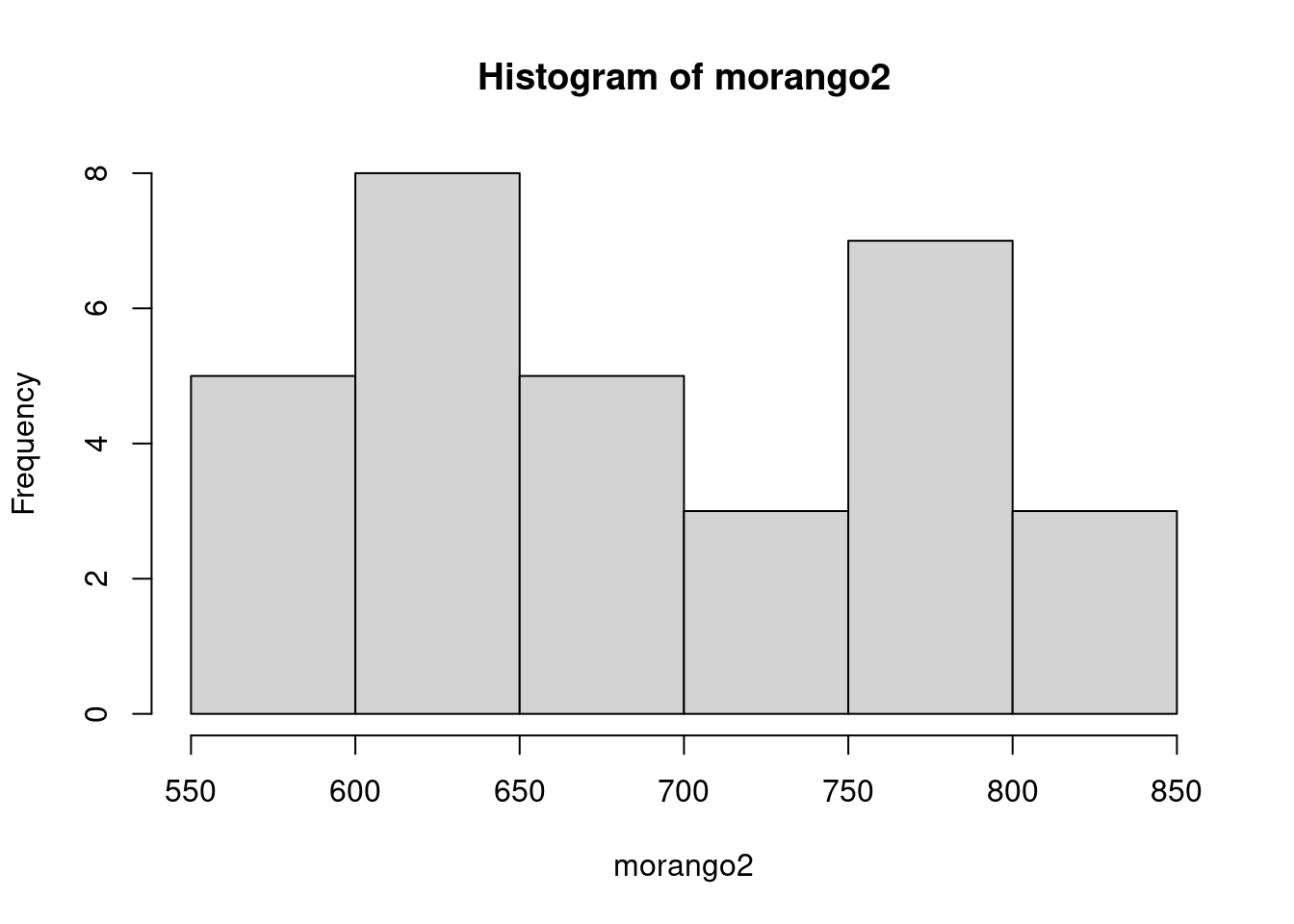
# Diagrama de ramo e folhas
stem(morango2)##
## The decimal point is 2 digit(s) to the right of the |
##
## 5 | 79999
## 6 | 0023334
## 6 | 556689
## 7 | 344
## 7 | 6777899
## 8 | 233
# Box-plot
boxplot(morango2)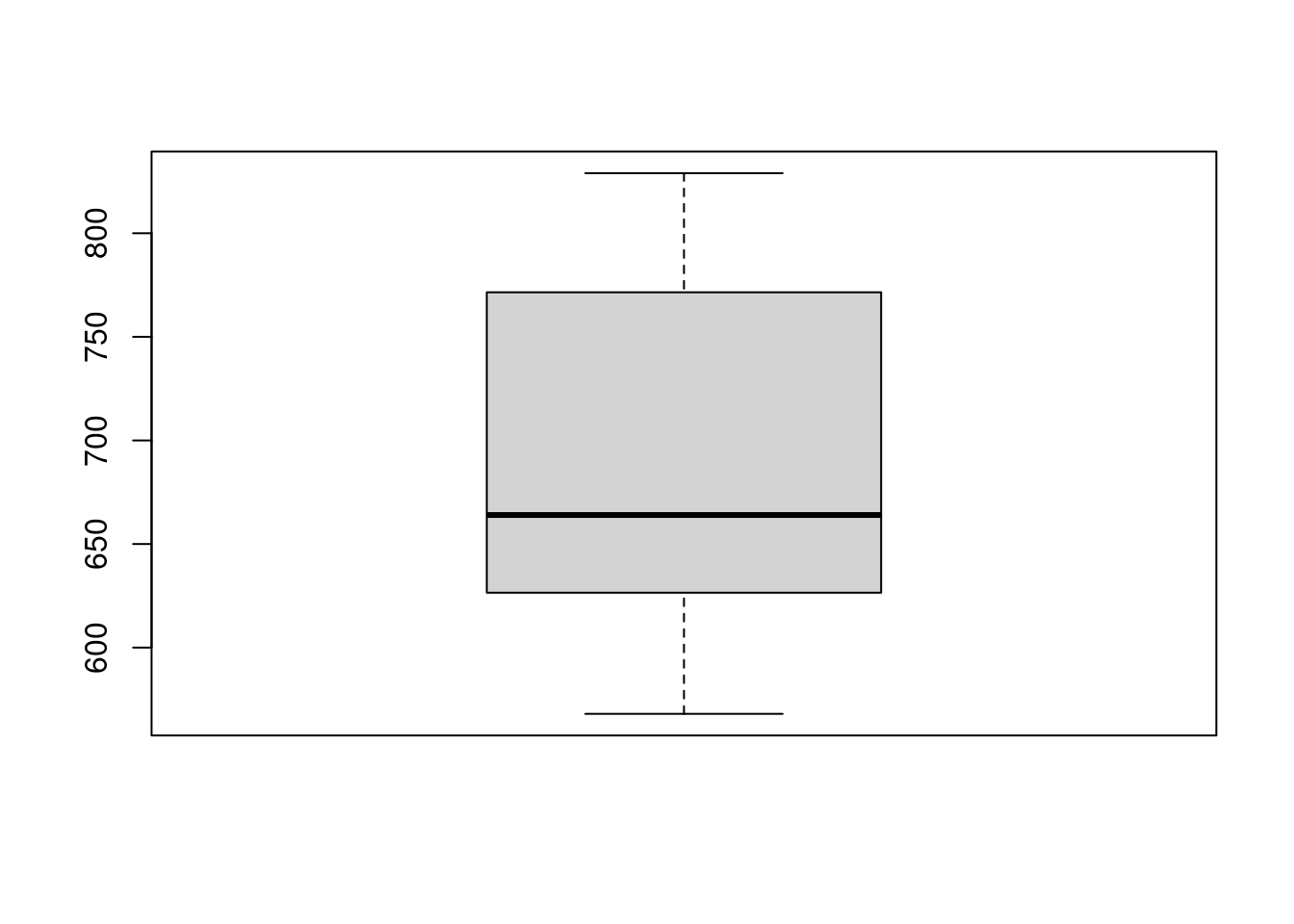
Agora, conseguimos ver que a distribuição é simétrica.
A média é 690.7 g e a mediana é 664 g.
O desvio-padrão é 83.4 e o resumo de cinco números é 568, 626.5, 664, 771.5, 829.
6.4 Comparação média/mediana
O exemplo 6.7 ilustra um fato importante sobre a média como medida de centro: ela é muito sensível a observações extremas, como em uma distribuição assimétrica ou na presença de valores atípicos.
Como a média não pode resistir à influência de observações extremas, dizemos que ela não é uma medida resistente de centro.
Ao contrário, a mediana é influenciada apenas pelo número total de pontos de dados e pelo valor numérico do ponto, ou pontos, localizado no centro da distribuição.
A média e a mediana de uma distribuição razoavelmente simétrica estão bem próximas uma da outra.
Se a distribuição for exatamente simétrica, a média e a mediana serão exatamente iguais.
Em uma distribuição assimétrica, a média está, em geral, numa posição mais extrema na cauda longa do que a mediana.
Assim como a média, o desvio-padrão s não é resistente. Algumas observações atípicas podem tornar s bastante grande.
Como o desvio-padrão mede a dispersão em torno da média, deve ser usado apenas quando a média for escolhida como a medida de centro.