6 Conceitos Básicos em Bioestatística

Antes de mergulharmos nas ferramentas e técnicas da bioestatística, é fundamental construirmos uma base sólida de conceitos básicos. Compreender esses conceitos é fundamental para o desenvolvimento de pesquisas robustas e para a interpretação correta dos resultados. Dominar esses conceitos básicos permitirá que você navegue com segurança pelos capítulos seguintes, aplicando as ferramentas da bioestatística de forma eficiente e crítica.

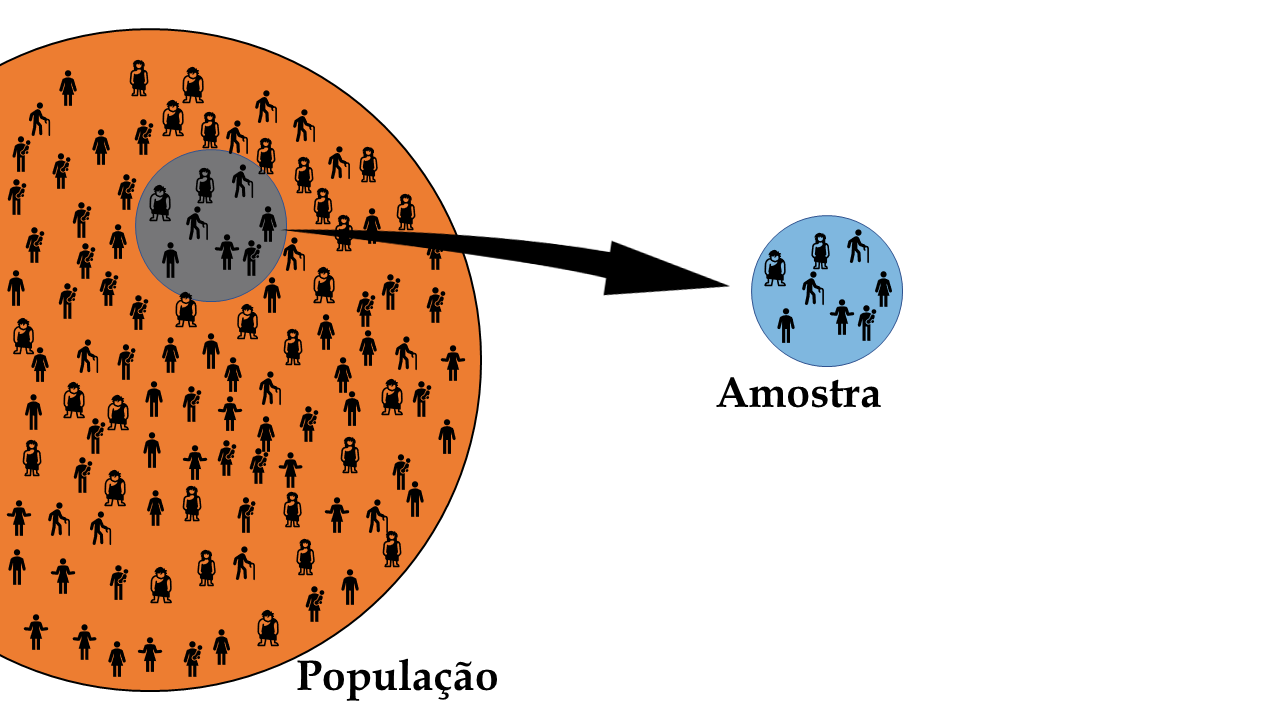
6.1 População e amostra

A compreensão da diferença entre população e amostra é fundamental para a aplicação correta das técnicas da bioestatística.

População

A população representa o conjunto completo de elementos (indivíduos, objetos, eventos) que compartilham uma característica de interesse. Frequentemente, há infinitos elementos em uma população ou, então, tantos que não conseguimos estudar cada um deles.

Exemplo 6.1 (Exemplos de população) Uma população pode ser definida como todos os indivíduos de uma espécie em uma área específica, todas as plantas de milho em uma área de cultivo, todos os indivíduos de uma espécie de peixe em um lago, todos os frutos de café em um cafezal, etc.

Amostra

Uma amostra é um subconjunto da população, selecionado para representar as características da população como um todo. A amostragem é essencial quando o estudo da população inteira é inviável ou impraticável, seja por restrições de tempo, custo ou acessibilidade.

Exemplo 6.2 (Exemplos de amostra) Por exemplo, em uma plantação com milhares de pés de milho, podemos estudar “apenas” 50 plantas selecionadas aleatoriamente para estimar a produtividade média da lavoura. Da mesma forma, em um lago com centenas de indivíduos de uma espécie de peixe, podemos amostrar “apenas” 10 indivíduos para estudar o acúmulo de metais pesados nos tecidos.

6.2 Variáveis

Uma variável é uma característica, propriedade ou atributo que pode variar entre os elementos de uma população ou amostra. Em outras palavras, é algo que pode ser medido ou observado e que assume diferentes valores.

Exemplo 6.3 (Crescimento de árvores em uma floresta) Em um estudo sobre o crescimento de árvores em uma floresta, pesquisadores avaliaram 10 árvores de Araucaria angustifolia. Entre as variáveis de interesse, estão:

Altura da árvore (em metros)
Diâmetro do tronco (em centímetros)
Idade da árvore (em anos)
Condição da árvore (saudável, doente, morta)

6.2.1 Tipos de variáveis

As variáveis podem ser classificadas em dois tipos principais:

Qualitativa ou Categórica: Posiciona um indivíduo em um de diversos grupos ou categorias. Também podemos dizer que expressa uma qualidade do indivíduo.
- Nominais: Representam categorias sem ordem intrínseca, como a cor de uma flor, sexo de um mamífero, formato de uma folha, tipo de solo, etc.
- Ordinais: Representam categorias com uma ordem natural, como a escala de Likert (por exemplo, classifique de 0 a 5, com 0 para realmente não gosto e 5 para realmente gosto), comportamento de um animal (agressivo, neutro, submissivo), estágio de desenvolvimento de uma planta (plântula, vegetativo, florescimento, frutificação), etc.
Quantitativa ou Numérica: Assume valores numéricos e operações aritméticas, como adição e média, podem ser realizadas.
- Discretas: Assumem valores inteiros e contáveis, como o número de pétalas em uma flor, número de filhotes de uma ave, etc.
- Contínuas: Podem assumir qualquer valor em um intervalo, como o comprimento do caule de uma planta, temperatura corporal de um primata, etc.

Exemplo 6.4 (Qualidade da água) Em um estudo sobre a qualidade da água de um rio, quais das variáveis são categóricas e quais são quantitativas?

pH da água
Concentração de oxigênio dissolvido
Presença de coliformes fecais
Turbidez da água
Temperatura da água (°C)
Concentração de nitrato (mg/L)
Velocidade da correnteza (m/s)
Presença de espécies indicadoras de poluição

Solução

pH da água (quantitativa contínua).
Concentração de oxigênio dissolvido (quantitativa contínua).
Presença de coliformes fecais (qualitativa nominal - presente/ausente).
Turbidez da água (qualitativa ordinal - baixa, média, alta).
Temperatura da água (°C): Quantitativa contínua.
Concentração de nitrato (mg/L): Quantitativa contínua.
Velocidade da correnteza (m/s): Quantitativa contínua.
Presença de espécies indicadoras de poluição: Qualitativa nominal.

Dependendo de como a varivel é coletada ou medida, a sua classificação pode mudar. Em muitas situações, variáveis categóricas podem ser transformadas em variáveis quantitativas e vice-versa.

6.2.2 Variáveis derivadas

A maior parte das variáveis são obtidas por meio de medidas e observações diretas. No entanto, há uma importante classe de variáveis denominadas derivadas, criadas a partir de duas ou mais variáveis originais. Alguns exemplos são: razão, porcentagem, índice e taxa.

Exemplo 6.5 (Variáveis derivadas)

Índice de Massa Corporal (IMC) = peso (kg) / altura (m)²
Taxa de crescimento de uma planta = (altura final - altura inicial) / tempo

6.3 Estatística Descritiva vs. Inferencial

A estatística pode ser dividida em duas grandes áreas:

Estatística Descritiva:
- Objetivo: Descrever, organizar e resumir dados.
- Ferramentas: Tabelas, gráficos, medidas de tendência central (média, mediana, moda), medidas de dispersão (variância, desvio padrão).
Estatística Inferencial:
- Objetivo: Generalizar conclusões de uma amostra para a população.
- Ferramentas: Estimação de parâmetros, testes de hipóteses, intervalos de confiança.

Exemplo 6.6 (Produção de soja) Em um estudo sobre a produção de soja em uma região, a estatística descritiva seria usada para calcular a produção média por hectare, a variabilidade da produção entre as fazendas e criar gráficos para visualizar a distribuição dos dados. A estatística inferencial seria usada para estimar a produção total de soja na região com base na amostra de fazendas estudadas e para testar hipóteses sobre os fatores que influenciam a produção.

6.4 Estudo Observacional vs. Experimental

Estudo Observacional:
Os pesquisadores observam e medem as variáveis sem intervir no sistema.
Objetivo: Descrever e analisar relações entre variáveis.

Exemplo 6.7 (Um estudo observacional) Um estudo acompanhou 130 mil pessoas, que bebiam cerveja, vinho ou licor, durante 12 anos. Foram documentados os casos de infarto do miocárdio. O estudo mostrou que ocorriam 35% menos mortes por infarto entre os que tomavam vinho (tinto ou branco) comparado aos que bebiam cerveja.

Estudo Experimental:
Os pesquisadores manipulam uma ou mais variáveis (fatores) e observam o efeito na variável resposta.
Objetivo: Investigar relações de causa e efeito.

Exemplo 6.8 (Um estudo experimental) Um agrônomo afirma que um novo fertilizante orgânico, em comparação com a marca líder, aumenta a produção e o tamanho dos tomates. Para o teste dessa afirmativa, plantas de tomate são associadas aleatoriamente a cada um dos fertilizantes: um grupo é cultivado com o fertilizante líder e o outro grupo, com o novo fertilizante orgânico. Na época da colheita, registra-se o tamanho e a massa de cada tomate, juntamente com o total de tomates por planta. Os dados coletados desse experimento são usados para comparar os dois fertilizantes.

6.5 Confundimento

O confundimento ocorre quando vários fatores juntos contribuem para um efeito, mas nenhuma causa única pode ser isolada.

Voltando ao exemplo do vinho… (Exemplo 6.7)

As pessoas que preferem vinho são diferentes daquelas que bebem cerveja. Os bebedores de vinho, como um grupo, são mais ricos e mais bem educados, comem mais frutas e vegetais e menos frituras. Sua dieta contém menos gordura e menos colesterol. A variável explicativa (Qual tipo de bebida alcoólica você bebe com mais frequência?) é confundida com muitas variáveis ocultas (educação, riqueza, alimentação e outras).

Voltando ao exemplo do tomate… (Exemplo 6.8)

Suponha que as plantas de tomate em um dos grupos sejam irrigados com mais frequência e/ou expostos a mais luz do sol. Se os pés de tomate que receberam o novo fertilizante estiverem sob essas condições diferentes (favoráveis) de crescimento, uma diferença na produção não poderá ser atribuída, unicamente, ao novo produto.

O confundimento é um dos principais desafios em estudos observacionais, e pode levar a conclusões errôneas sobre a relação entre as variáveis. Para minimizar o impacto do confundimento e aumentar a validade das suas conclusões, algumas estratégias incluem um cuidado redobrado com o delineamento do estudo e no uso das técnicas de análise estatística.

Exemplo 6.9 (Confundimento) Em um estudo sobre o efeito da poluição do ar na saúde respiratória, a idade pode ser um fator de confundimento, pois pessoas mais velhas tendem a ter maior risco de problemas respiratórios. Para lidar com esse confundimento, poderíamos utilizar as seguintes estratégias:

Delineamento: Restringir a participação no estudo a indivíduos de uma faixa etária específica ou emparelhar indivíduos com base na idade.
Análise: Utilizar a análise estratificada para comparar o efeito da poluição em diferentes faixas etárias ou incluir a idade como variável no modelo de regressão multivariada.

Ao combinar estratégias de delineamento e análise, você pode minimizar o impacto do confundimento e obter resultados mais confiáveis e válidos.