8  Gráficos estatísticos

Uma imagem vale mais que mil palavras

Os gráficos estatísticos são utilizados para fazer uma representação visual dos dados. São elaborados para serem vistos por você e por outras pessoas, por isso, sempre haverá um certo nível de subjetividade na interpretação do gráfico.

Não há (muitas) regras na elaboração dos gráficos, pelo contrário, temos liberdade para elaborá-los das forma que melhor nos convém. No entanto, existem guias gerais bem estabelecidas que facilitam o processo de escolha do tipo de gráfico mais adequado para o seu conjunto de dados. Em outras palavras, uma boa metodologia aplicada na construção dos gráficos é extremamente útil para seu correto entendimento e interpretação, seja qual for o público alvo.

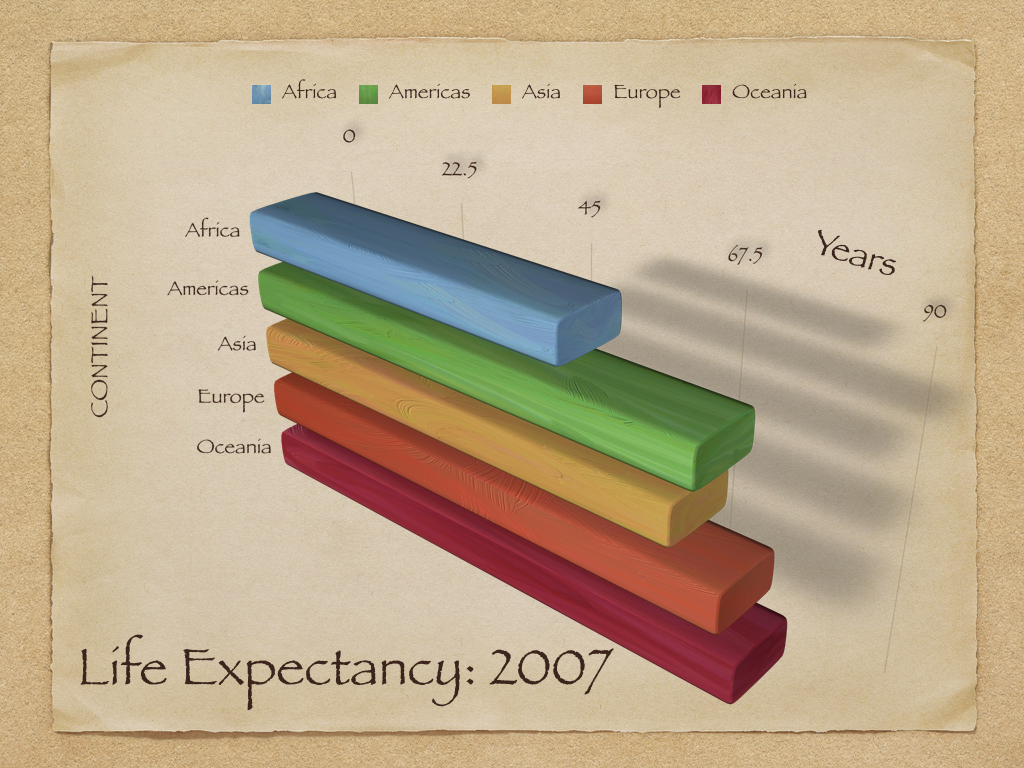
Na Figura 8.1 vemos um exemplo de um gráfico ruim. Há uma quantidade considerável de poluição visual; as barras são difíceis de comparar devido à perspectiva “3D”; os rótulos estão duplicados, na legenda e no eixo vertical; as sombras não acrescentam nenhuma informação; a escolha das cores não foi muito bem feita.

Figura 8.1: Um gráfico com poluição visual e de gosto duvidoso.

8.1 O pacote ggplot2

O pacote ggplot2 foi criado por Hadley Wickham baseado em um conceito denominado “Gramática de Gráficos” (Grammar of Graphics).

De um modo geral, a criação de gráficos com o ggplot2 executa o mapeamento (mapping) dos dados para propriedades estéticas (aes) e geométricas (geom_*). Ainda, podem ser executadas transformações estatísticas (stat_*) e divisões (facet_*). Todas essas camadas combinadas irão resultar no gráfico final.

O primeiro passo é chamar a funçao ggplot (sem o número 2 no final!). O argumento data recebe o conjunto de dados (data.frame) que contém os valores.

Para este primeiro exemplo, vamos utilizar o conjunto de dados iris.

Vamos mapear o eixo x para a variável Sepal.Length (Comprimento da Sépala) e o eixo y para a variável Sepal.Width (Largura da Sépala). Fica assim:

pacman::p_load("ggplot2") # instalar e carrega o pacote ggplot2

ggplot(
  data = iris,
  mapping = aes(x = Sepal.Length, y = Sepal.Width)
)
Figura 8.2: Pano de fundo para um gráfico criado com o ggplot2 usando o dataset iris

Ops, o gráfico resultante está vazio! O que aconteceu? Esta função cria apenas o “pano de fundo” para o gráfico, uma vez que ainda não definimos nenhuma geometria para preenchê-lo.

Para completar o gráfico, basta digitar o sinal de adição + e chamar alguma função do tipo geom_*, por exemplo, geom_point para um gráfico de pontos 1. Na prática, estamos adicionando (+) mais uma camada ao gráfico.

ggplot(
  data = iris,
  mapping = aes(x = Sepal.Length, y = Sepal.Width)
) +
  geom_point()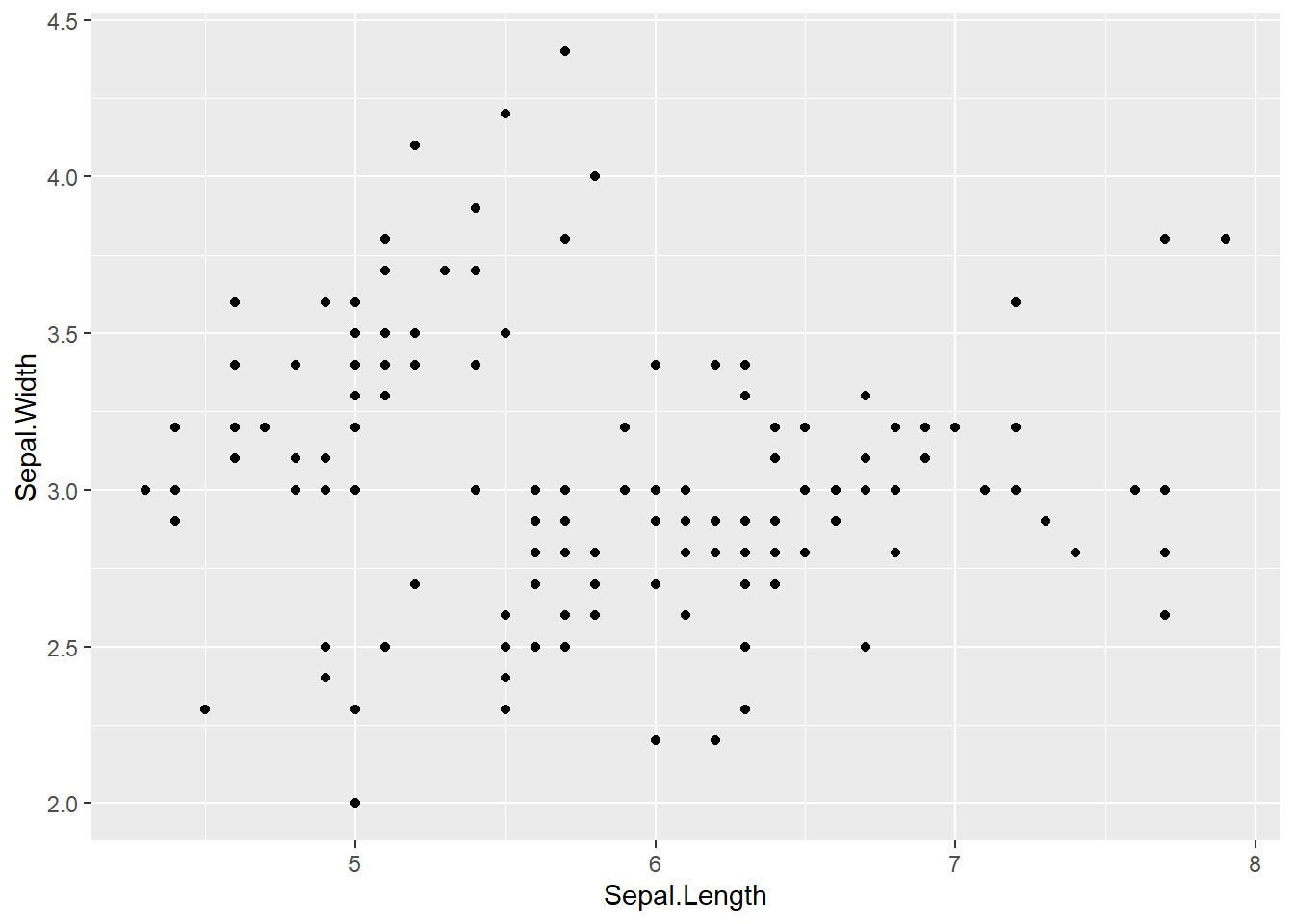
Figura 8.3: Gráfico de dispersão entre o Comprimento da Sépala e a Largura da Sépala.

Em geral, todos os gráficos produzidos com o ggplot seguem praticamente a mesma receita:

ggplot(
  data = <data>,
  mapping = aes(x = <variável x>, 
                y = <variável y>,
                <...> = <...>)
) +
  geom_*(<...>) +
  <...>

Para simplificar ainda mais o código, é possível suprimir o nome dos argumentos data e mapping, pois são argumentos muito comuns em todos os gráficos criados com o ggplot2. Por isso, de agora em diante, neste livro, estes nomes não serão mais escritos.

ggplot(
  iris,
  aes(x = Sepal.Length, y = Sepal.Width)
) +
  geom_point()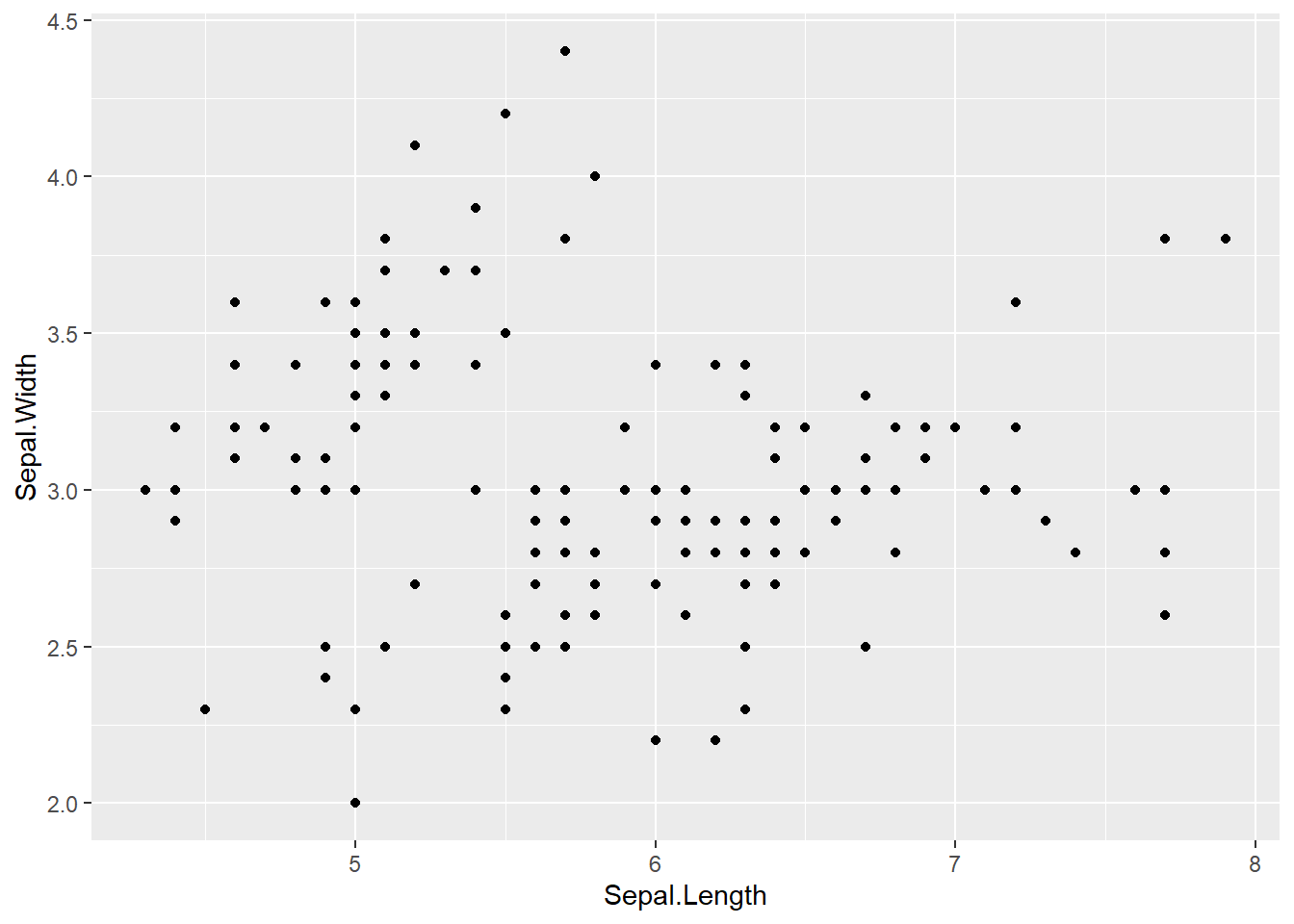
Figura 8.4: Outro código que produz um gráfico idêntico ao da Figura anterior (com dataset iris)

8.1.1 Criando gráficos do ggplot como objetos

Uma forma bastante conveniente de trabalhar com os gráficos é armazenar em objetos.

p_iris <- ggplot(
  iris,
  aes(x = Sepal.Length, y = Sepal.Width)
)

Neste código, criamos um objeto denominado p_iris que contém as informações básicas do gráfico. Na sequência, podemos adicionar mais elementos neste mesmo gráfico apenas adicionando (+) alguma função ao objeto.

p_iris +
  geom_point()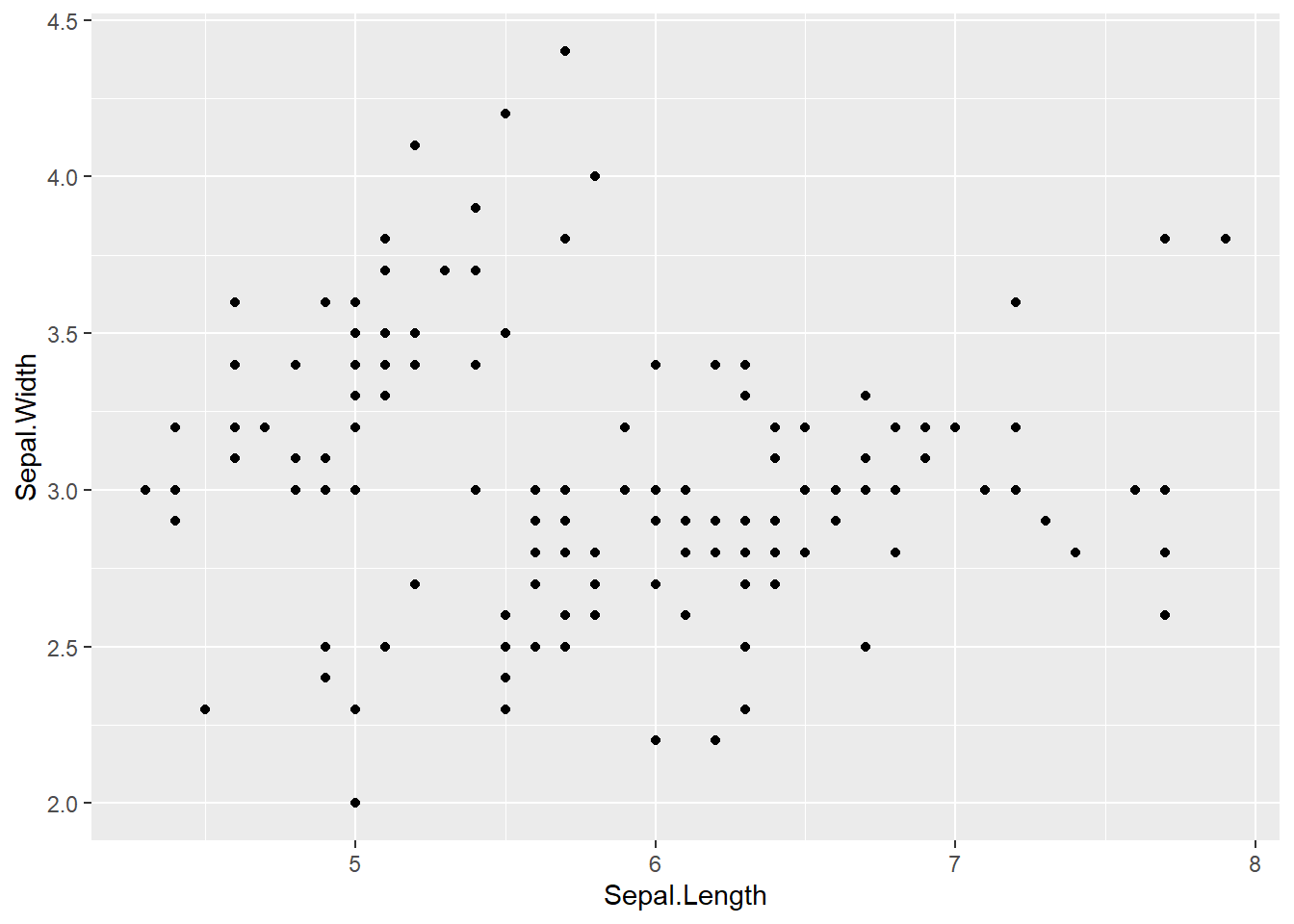
Figura 8.5: Adicionando uma camada geom_point() ao objeto p_iris 
p_iris +
  geom_smooth() # Adiciona uma linha de tendência suavizada
`geom_smooth()` using method = 'loess' and formula = 'y ~ x'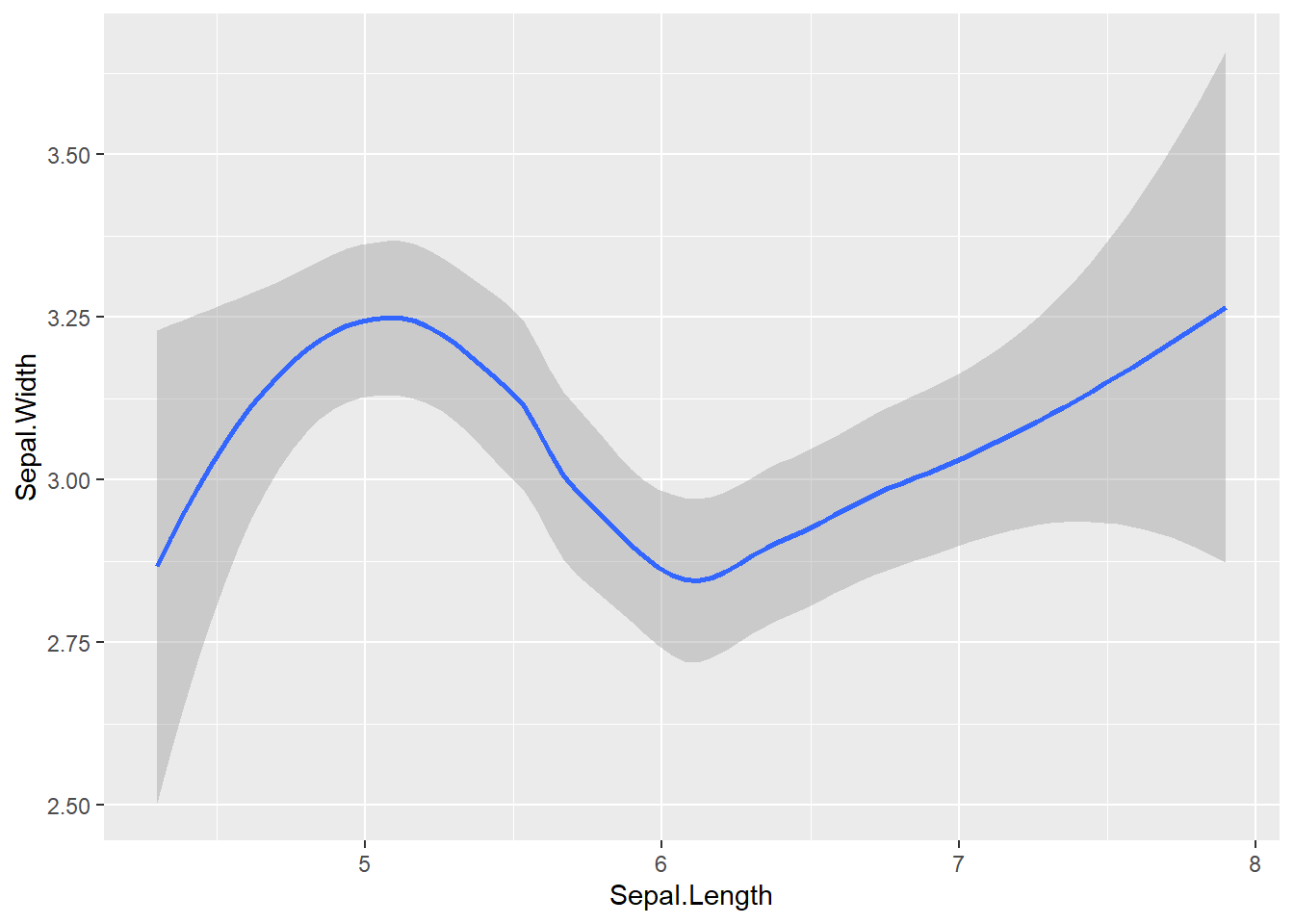
Figura 8.6: Adicionando uma camada geom_smooth() ao objeto p_iris 
p_iris +
  geom_point() + # Adiciona os pontos
  geom_smooth() # Adiciona a linha de tendência
`geom_smooth()` using method = 'loess' and formula = 'y ~ x'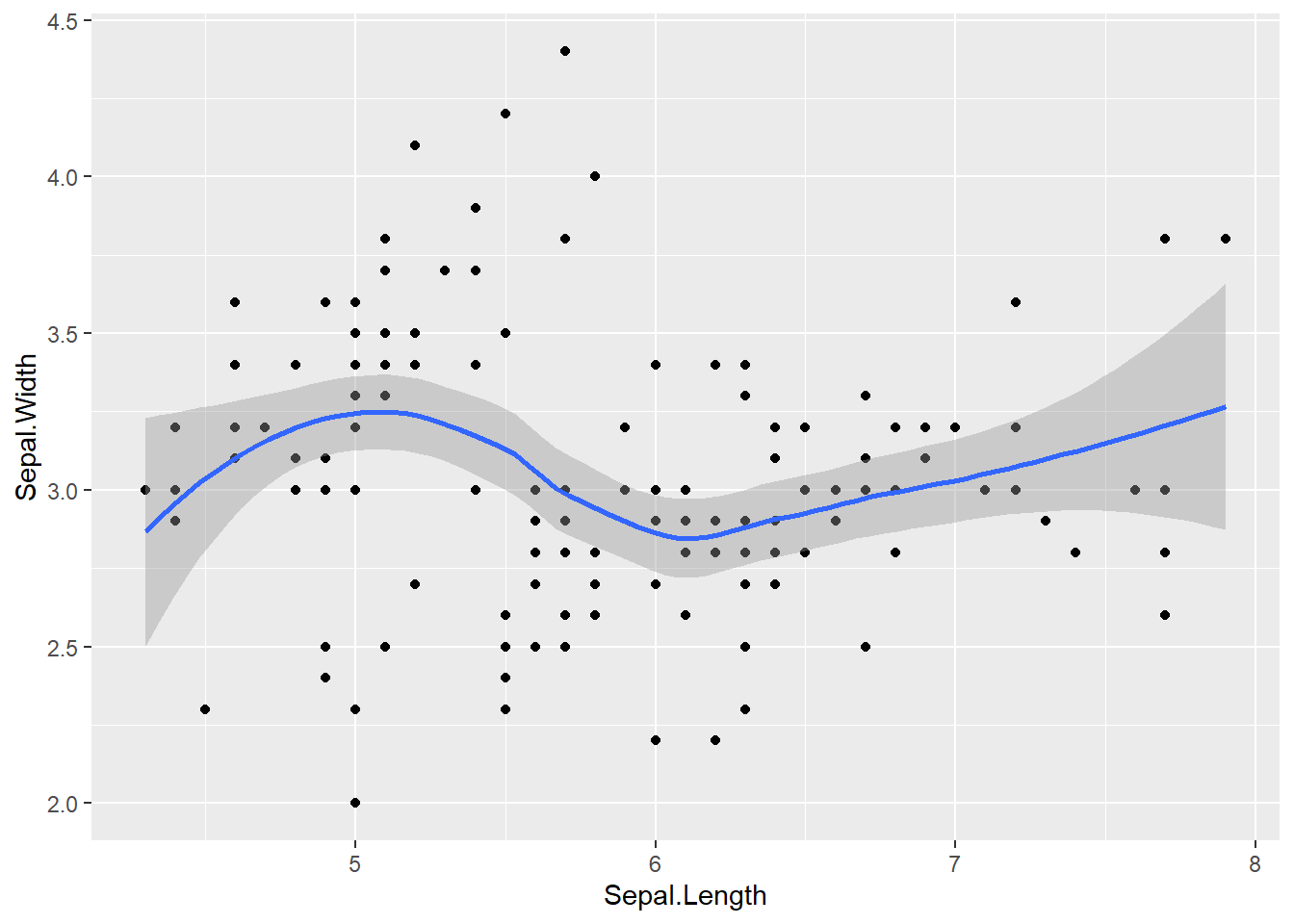
Figura 8.7: Adicionando várias camadas ao objeto p_iris

8.1.2 Personalizando os eixos

Muitas vezes precisamos personalizar os eixos do gráfico para aprimorar a visualização. A função labs permite alterar vários argumentos, como visto no exemplo a seguir:

p_iris +
  geom_point() +
  labs(
    x = "Comprimento da Sépala (cm)",
    y = "Largura da Sépala (cm)",
    title = "Relação entre Comprimento e Largura da Sépala",
    subtitle = "Cada ponto representa uma flor Iris",
    caption = "Fonte: dataset Iris (R)"
  )
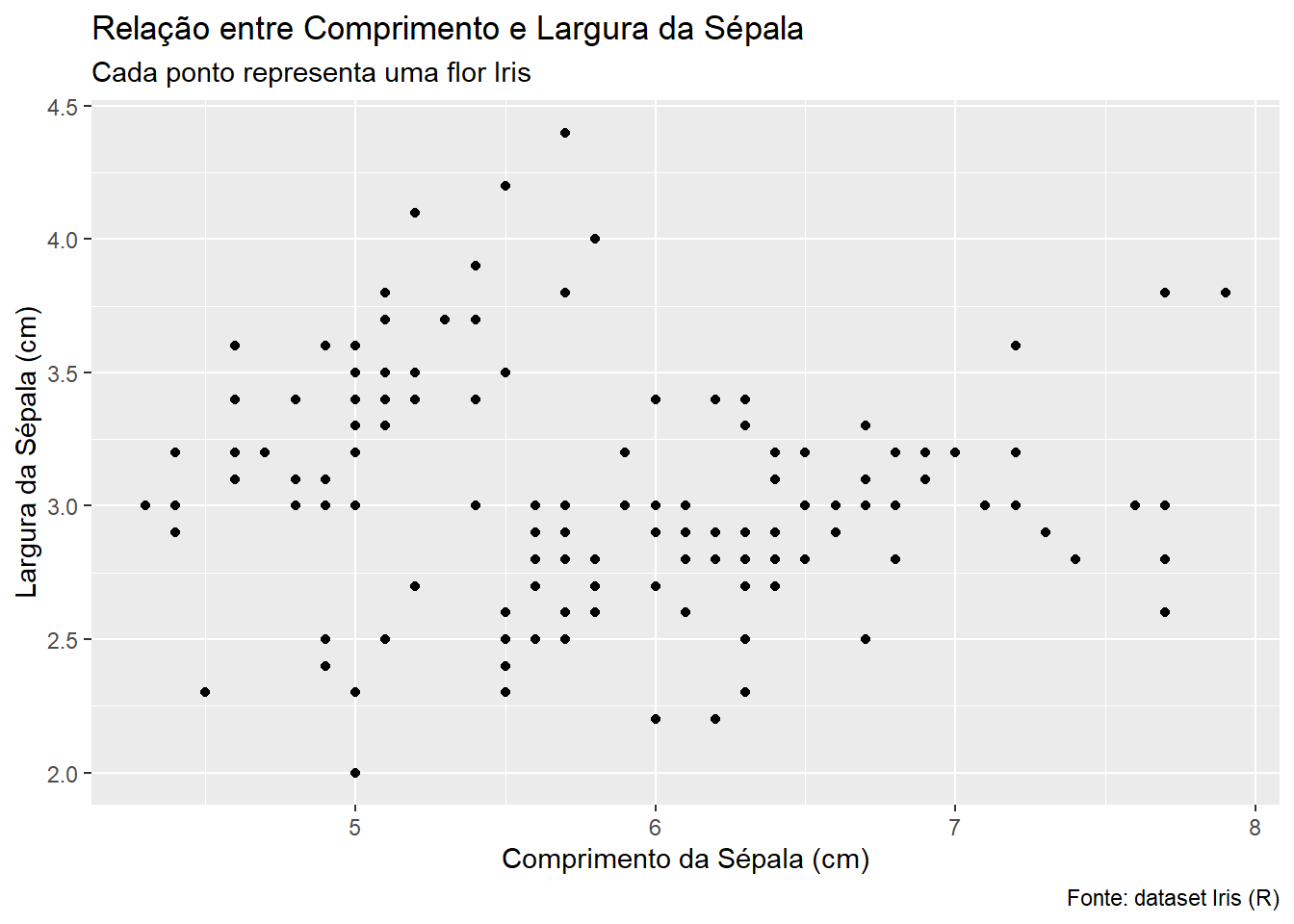
Figura 8.8: Personalizando o gráfico alterando o rótulo dos eixos e adicionando título e subtítulo (dataset iris).
  • x altera o rótulo do eixo x
  • y altera o rótulo do eixo y
  • title adiciona um título na parte superior
  • subtitle adiciona um subtítulo logo abaixo do título
  • caption rótulo que aparece no canto inferior direito

8.1.3 Mapeando atributos estéticos

Nesta seção, vamos estudar mais sobre os atributos estéticos. Em nosso primeiro gráfico, já utilizamos dois atributos de posição cartesiana: os eixos x e y. Entre vários outros atributos estéticos, vamos trabalhar com color e fill, que alteram cores (Apêndice B). No dataset iris, a variável Species é categórica e pode ser usada para colorir os pontos.

ggplot(
  iris,
  aes(
    x = Sepal.Length,
    y = Sepal.Width,
    color = Species # Mapeia a cor para a variável Species
  )
) +
  geom_point()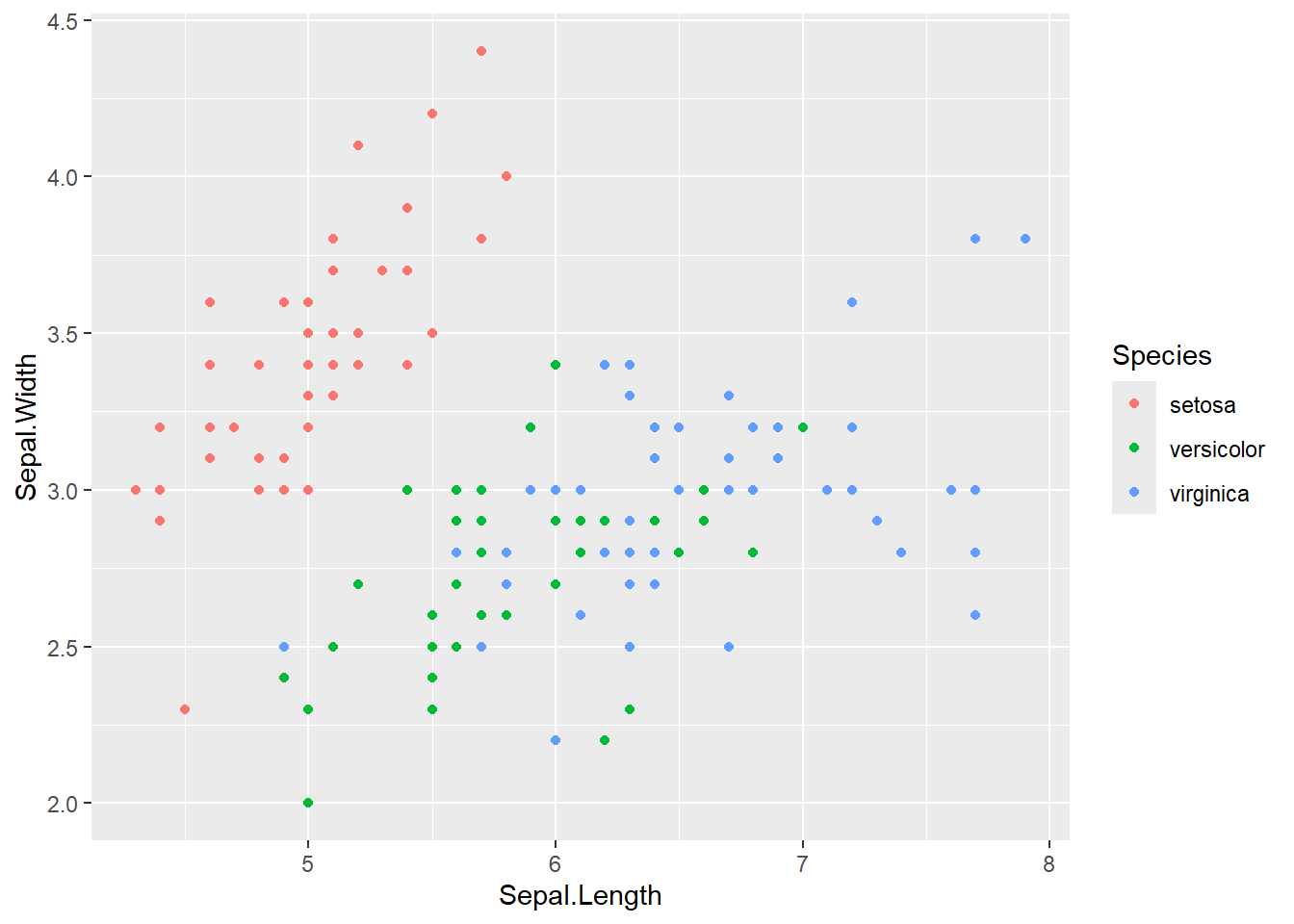
Figura 8.9: Mapeamento de cores diferentes para cada Espécie de Iris.

Vejam que ao mapear color para a variável Species, foram atribuídas cores aos pontos, uma cor diferente para cada espécie. Também foi adicionada uma legenda explicativa.

Na figura seguinte, vamos adicionar mais uma camada ao gráfico, a linha ajustada com geom_smooth.

ggplot(
  iris,
  aes(
    x = Sepal.Length,
    y = Sepal.Width,
    color = Species # Mapeia cor para pontos e linhas
  )
) +
  geom_point() +
  geom_smooth(method = "lm", formula = y ~ x, se = TRUE) # se=TRUE mostra o intervalo de confiança (padrão)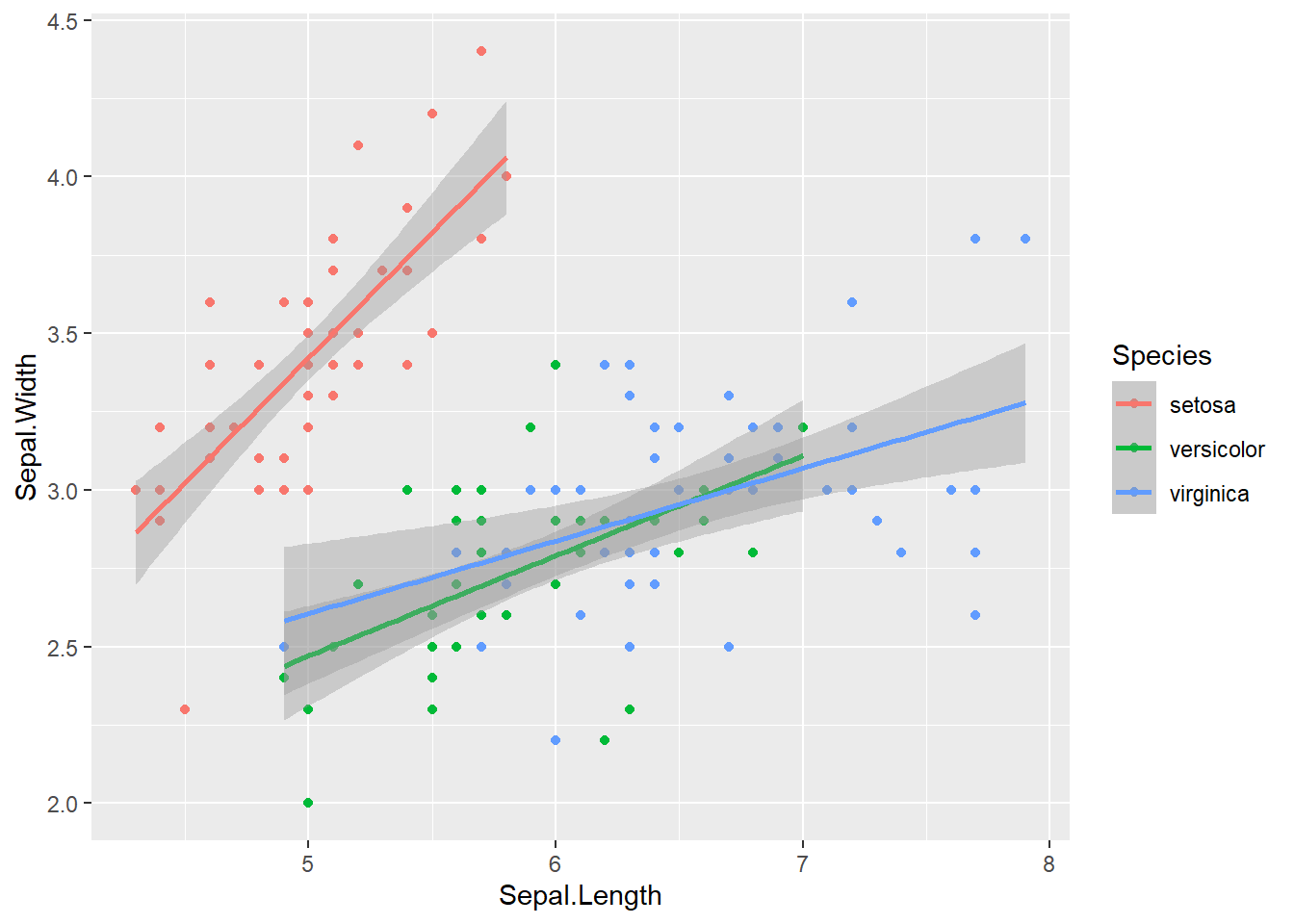
Figura 8.10: Adicionando linhas de tendência por espécie.

Veja que foi criada uma linha de ajuste para cada espécie. Isso acontece porque mapeamos o atributo color para Species no ggplot inicial, e tanto geom_point quanto geom_smooth herdam esse mapeamento. No entanto, a faixa do intervalo de confiança (se = TRUE) não acompanhou as cores automaticamente. Para colorir a área do intervalo de confiança, precisamos mapear Species também para o atributo fill.

ggplot(
  iris,
  aes(
    x = Sepal.Length,
    y = Sepal.Width,
    color = Species, # Cor para pontos e linhas
    fill = Species # Preenchimento para a área (intervalo de confiança)
  )
) +
  geom_point() +
  geom_smooth(method = "lm", formula = y ~ x, se = TRUE)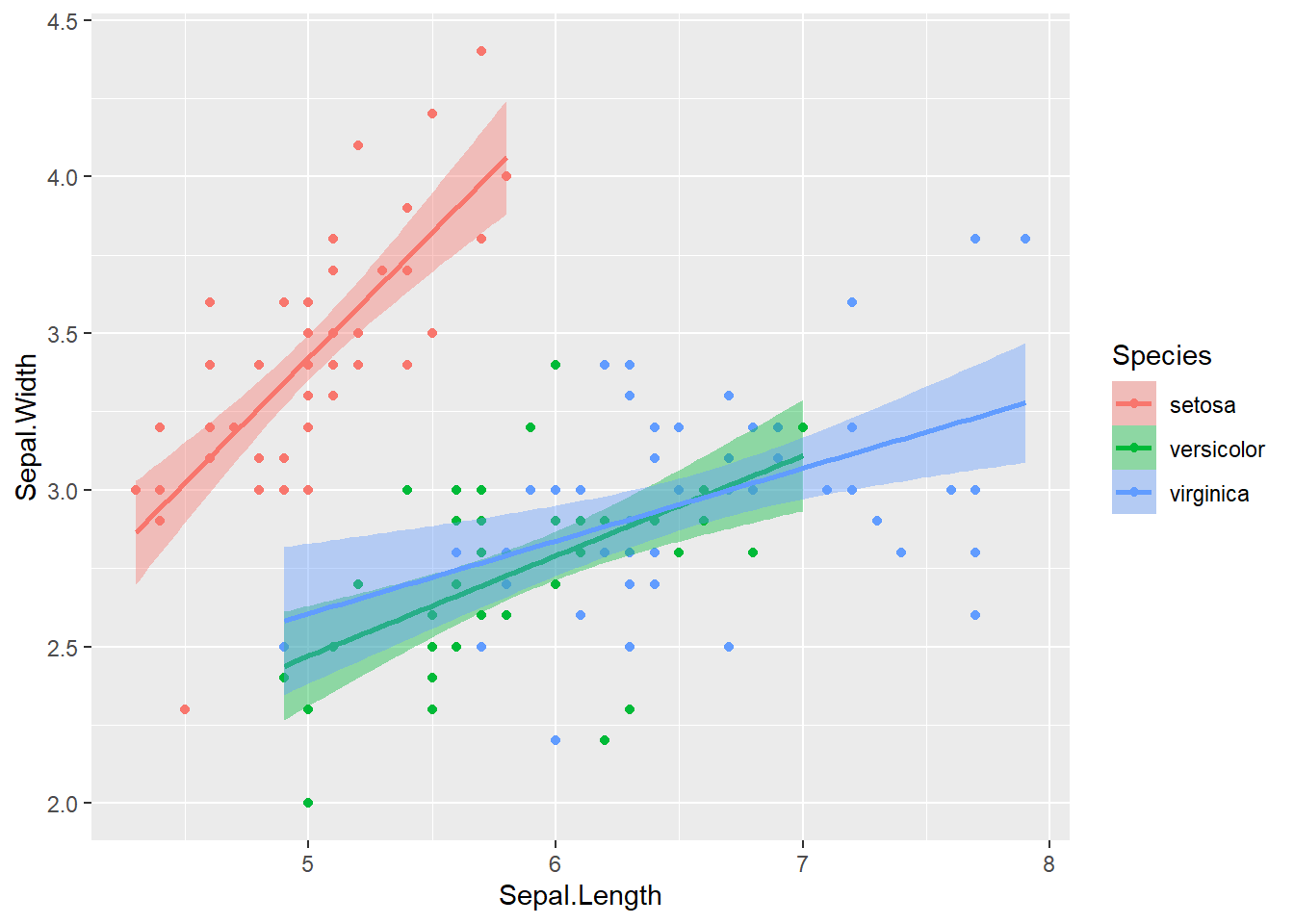
Figura 8.11: Colorindo também o intervalo de confiança das linhas de tendência.

8.1.4 Mapeando atributos em cada geom_*

Mas e se quisermos colorir os pontos por espécie, mas ajustar apenas uma linha de tendência geral para todos os dados? Para resolver esta situação, podemos mapear os atributos estéticos dentro de cada geometria específica, em vez de no ggplot inicial.

Por padrão, as funções geom_* herdam seus mapeamentos da funçao ggplot. Podemos alterar este comportamento mapeando a estética (aes) apenas dentro da função geom_* que queremos que se aplique.

ggplot(
  iris,
  aes( # Mapeamento base: apenas x e y
    x = Sepal.Length,
    y = Sepal.Width
  )
) +
  geom_point(aes(color = Species)) + # Mapeia 'color' SÓ para os pontos
  geom_smooth(method = "lm", formula = y ~ x) # Linha geral, sem mapeamento de cor herdado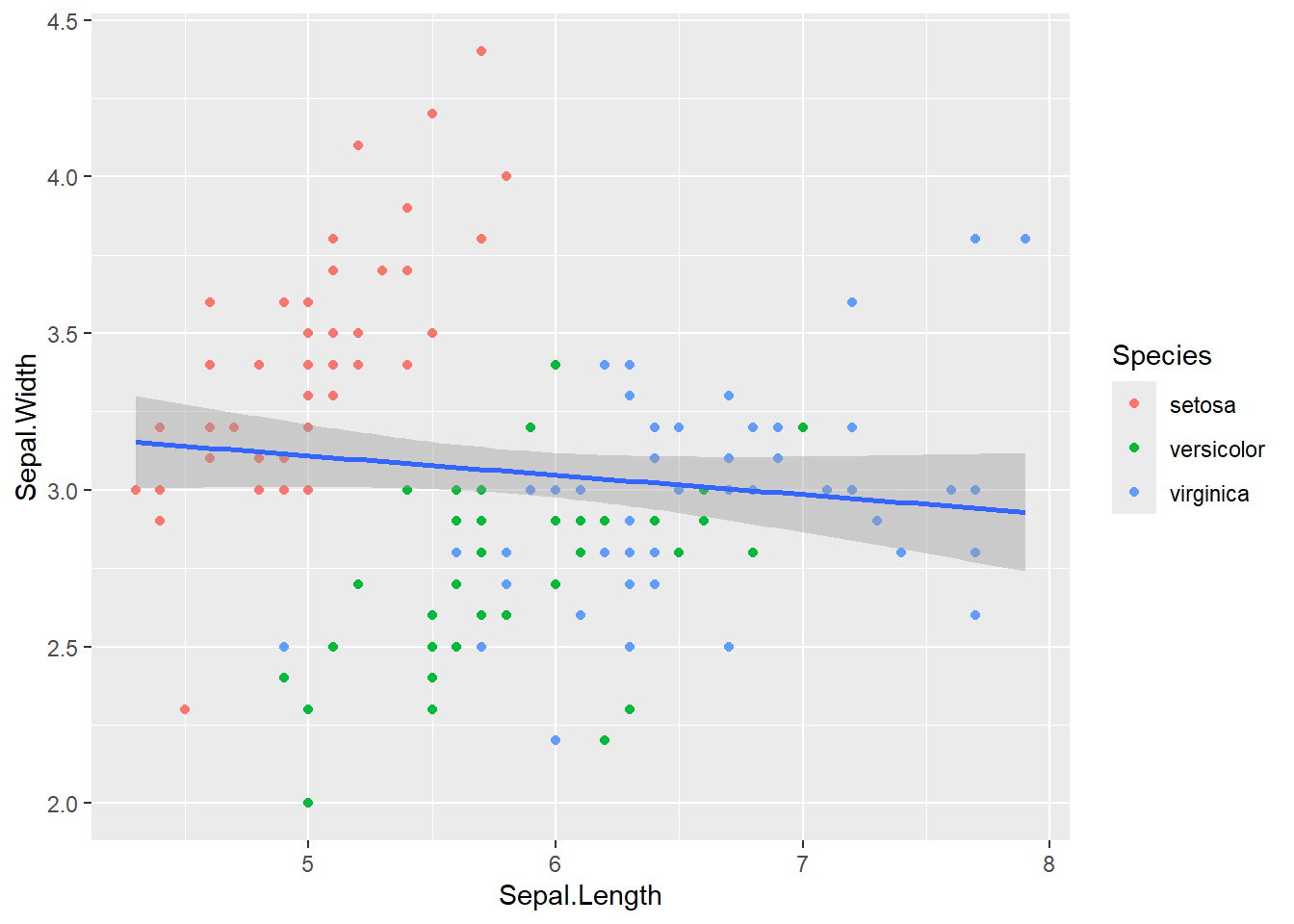
Figura 8.12: Pontos coloridos por espécie, mas apenas uma linha de tendência geral.

Também é possível mapear variáveis numéricas para atributos estéticos, como a cor. Por exemplo, podemos colorir os pontos de acordo com o Petal.Length (Comprimento da Pétala). Quando fazemos isso, a escala de cor produzida é um gradiente contínuo. A função scale_color_viridis_c() especifica a utilização da paleta de cor viridis para escalas contínuas.

ggplot(
  iris,
  aes(
    x = Sepal.Length,
    y = Sepal.Width
  )
) +
  geom_point(aes(color = Petal.Length)) + # Mapeia 'color' para Petal.Length
  geom_smooth(method = "lm", formula = y ~ x) +
  scale_color_viridis_c() # Usa a paleta viridis para cor contínua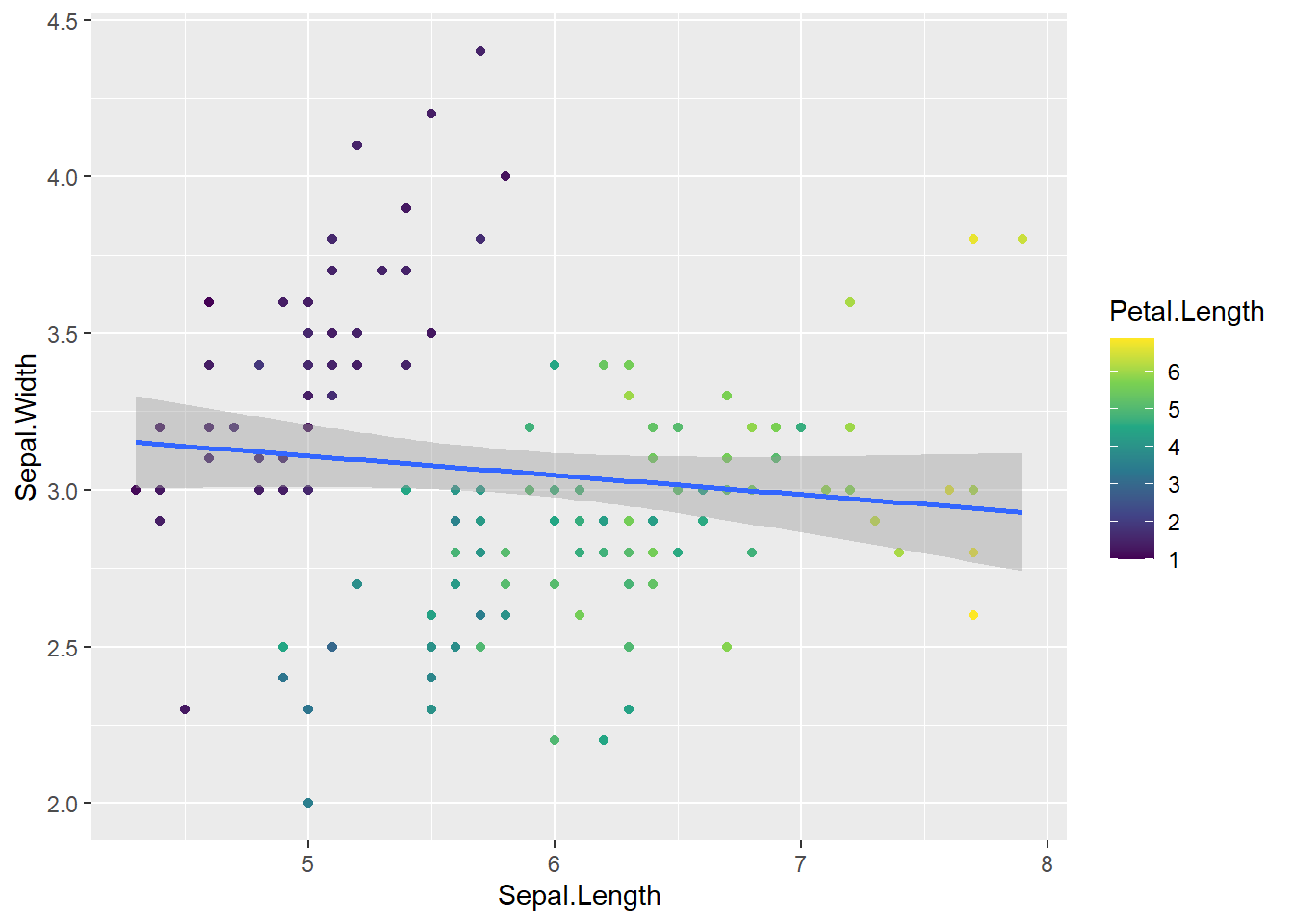
Figura 8.13: Pontos coloridos por Comprimento da Pétala (variável numérica).

8.1.5 Definindo atributos estéticos

Em algumas situações, nós apenas queremos definir um atributo estético com um valor fixo (ex: todos os pontos serem roxos), em vez de mapeá-lo para uma variável dos dados. Para isso, devemos definir estes atributos fora da função aes().

# Usando o objeto p_iris criado anteriormente
p_iris +
  geom_point(color = "purple") # 'color' está FORA do aes()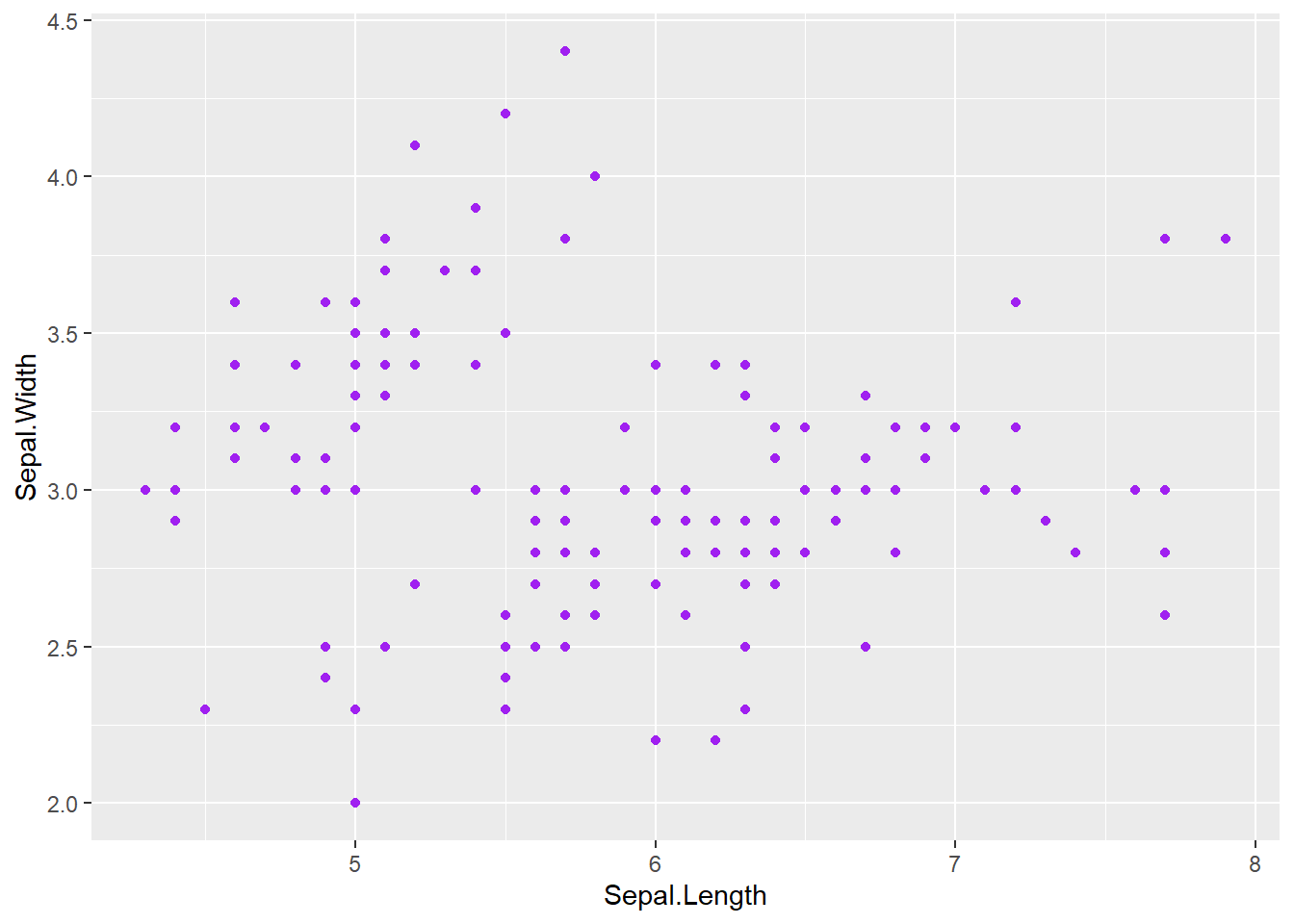
Figura 8.14: Definindo a cor dos pontos como roxa (fixa). 
p_iris +
  geom_point(shape = 8, size = 2, color = "tomato") # Define atributos fixos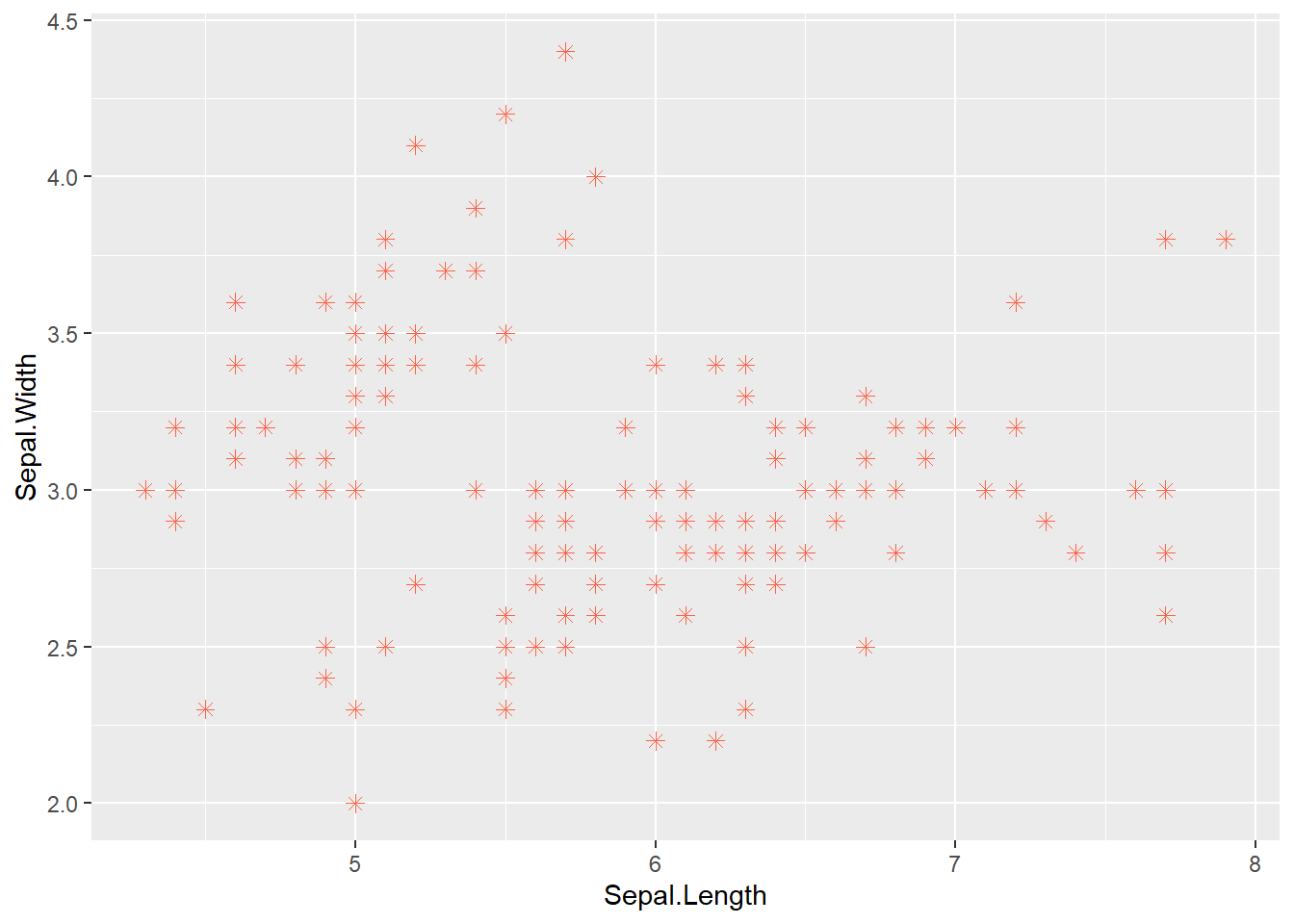
Figura 8.15: Definindo forma, tamanho e cor dos pontos. 
p_iris +
  geom_point(alpha = 0.5) + # Pontos semi-transparentes
  geom_smooth(color = "orange", linewidth = 1.5, method = "lm", formula = y ~ x, se = FALSE) # Linha laranja, mais grossa, sem IC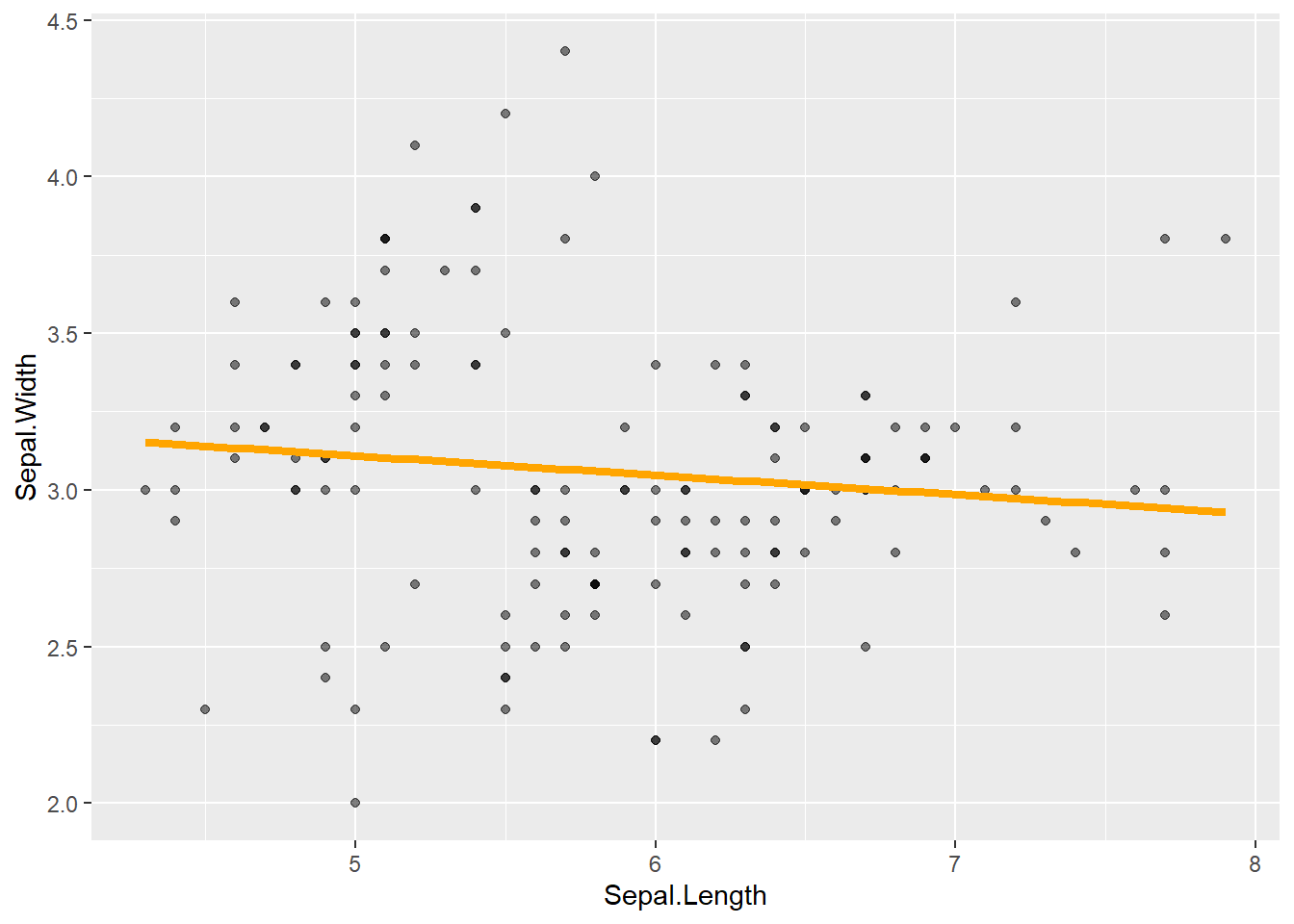
Figura 8.16: Definindo transparência (alpha) dos pontos e cor/espessura da linha.

8.2 Gráfico de barras

O gráfico de barras, que também pode ser chamado de gráfico de colunas, é um gráfico em que a altura das barras é proporcional ao valor por elas representado. Quando ordenado, também pode ser chamado de Gráfico de Pareto

Este tipo de gráfico é utilizado para representar os dados quando uma das variáveis é categórica ou numérica discreta. 2

Veja este gráfico de barras que representa a média do comprimentos de peixes machos e fêmeas (Seção A.4).

peixe %>%
  group_by(sexo) %>%
  summarise(med = mean(comp)) %>%
  ggplot(aes(x = sexo, y = med, fill = sexo)) +
  geom_bar(stat = "identity") +
  labs(
    x = "Sexo",
    y = "Média do Comprimento (cm)"
  ) +
  scale_x_discrete(labels = c("f" = "Fêmea", "m" = "Macho")) +
  scale_fill_discrete(labels = c("f" = "Fêmea", "m" = "Macho"), name = "Sexo")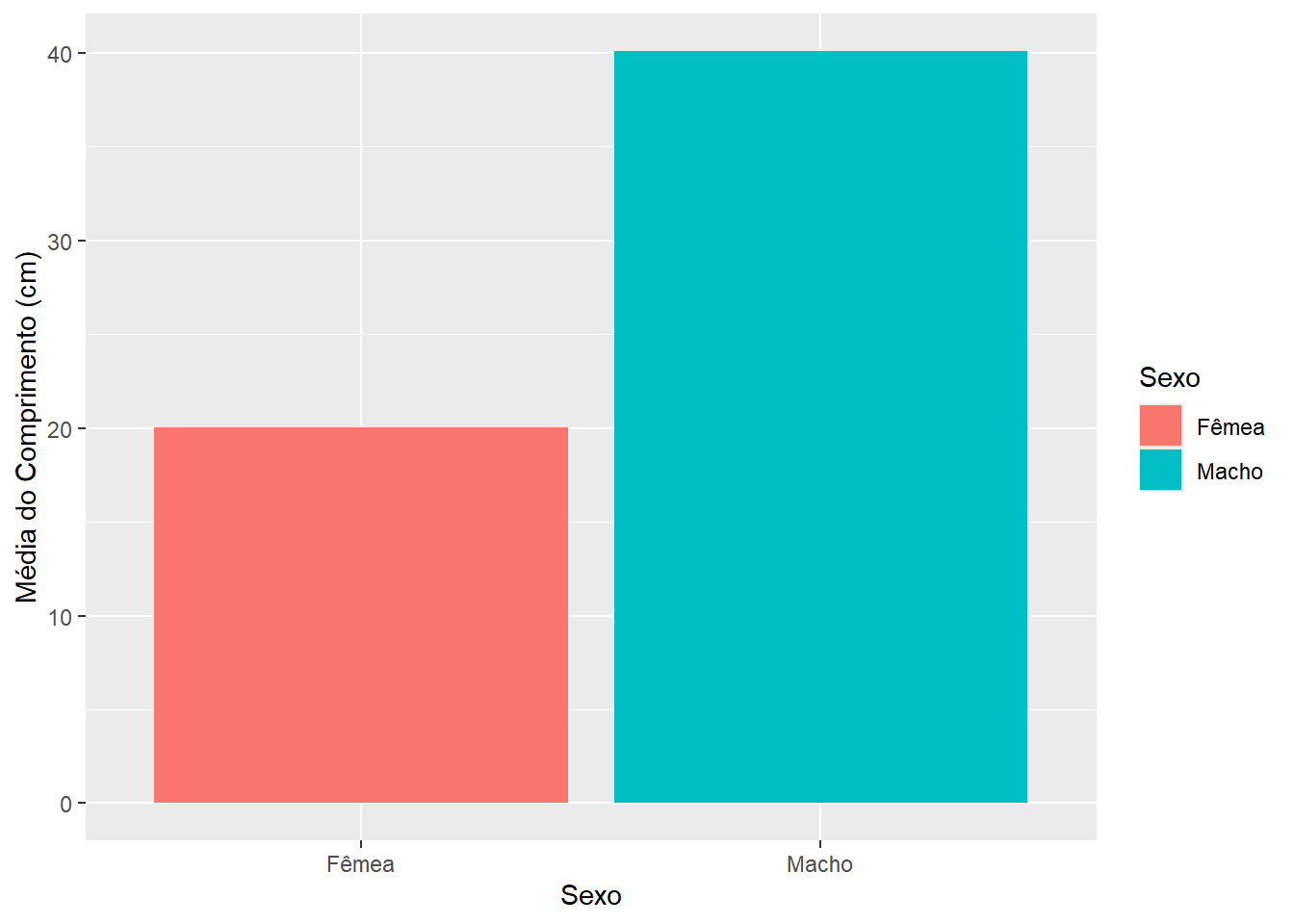
Figura 8.17: Média do comprimento (cm) de peixes machos e fêmeas apanhados em um rio.

8.3 Gráficos de dispersão

São utilizados para mostrar a relação entre duas variáveis numéricas contínuas. Para isso, são utilizados pontos que representam cada observação. A geometria para este tipo de gráfico é geom_point.

Veja este exemplo com os dados do conjunto iris.

ggplot(iris, aes(x = Petal.Length, y = Petal.Width)) +
  geom_point()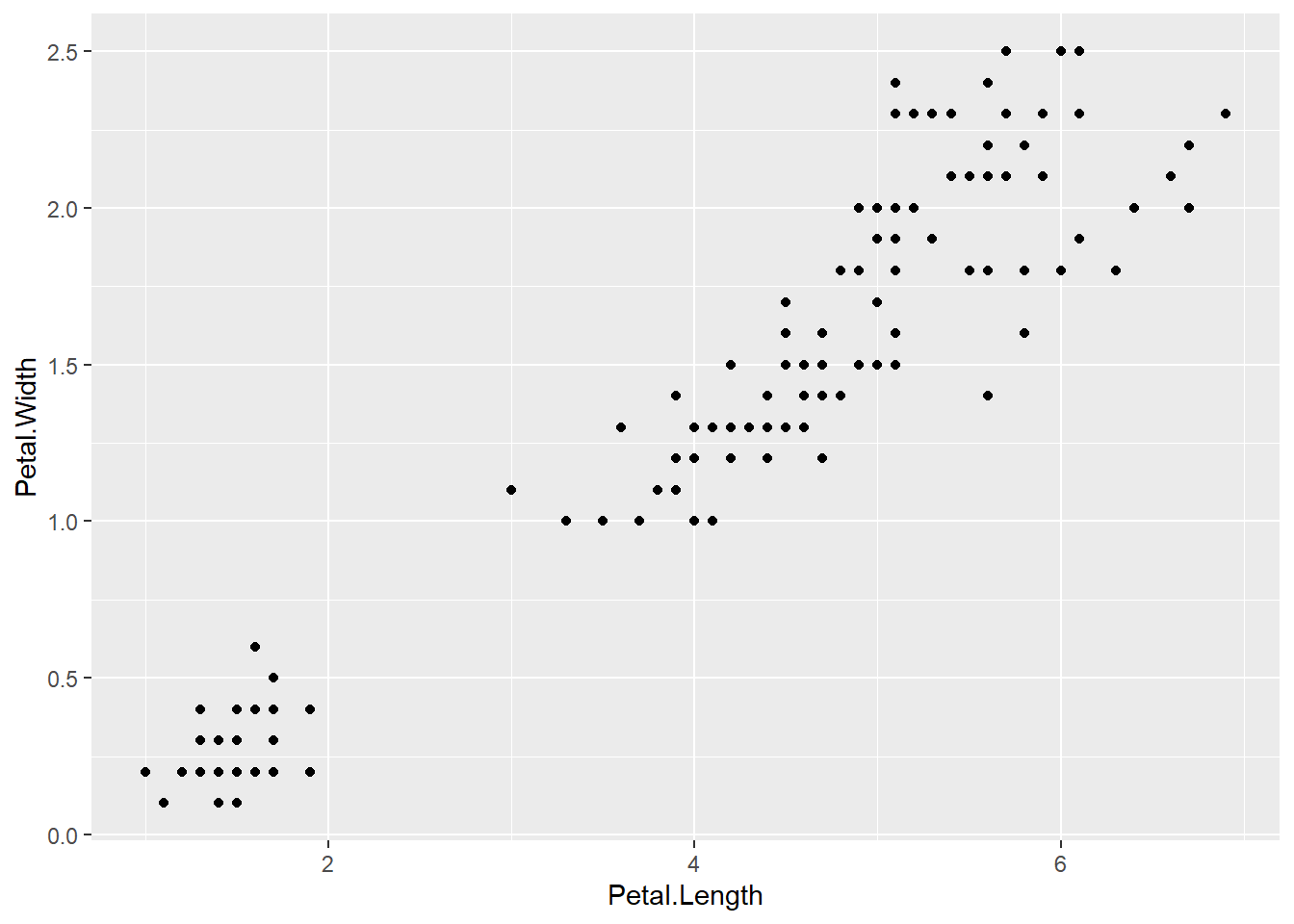
Figura 8.18: Relação entre o comprimento e largura de flores de espécies de Iris. Este é um gráfico de dispersão em que cada ponto representa um par de valores.

8.3.1 Linha de tendência

É comum visualizar a relação entre duas variáveis através de uma linha de tendência, representando os valores preditos por um modelo estatístico.

O pacote ggpmisc oferece uma alternativa integrada para essa tarefa, permitindo a adição da equação do modelo ajustado e do coeficiente de determinação (R2).

pacman::p_load("ggpmisc") # Carrega o pacote ggpmisc

ggplot(iris, aes(x = Petal.Length, y = Petal.Width)) +
  geom_point() +
  stat_poly_line(formula = y ~ x) +
  stat_poly_eq(mapping = use_label("eq", "R2"), formula = y ~ x)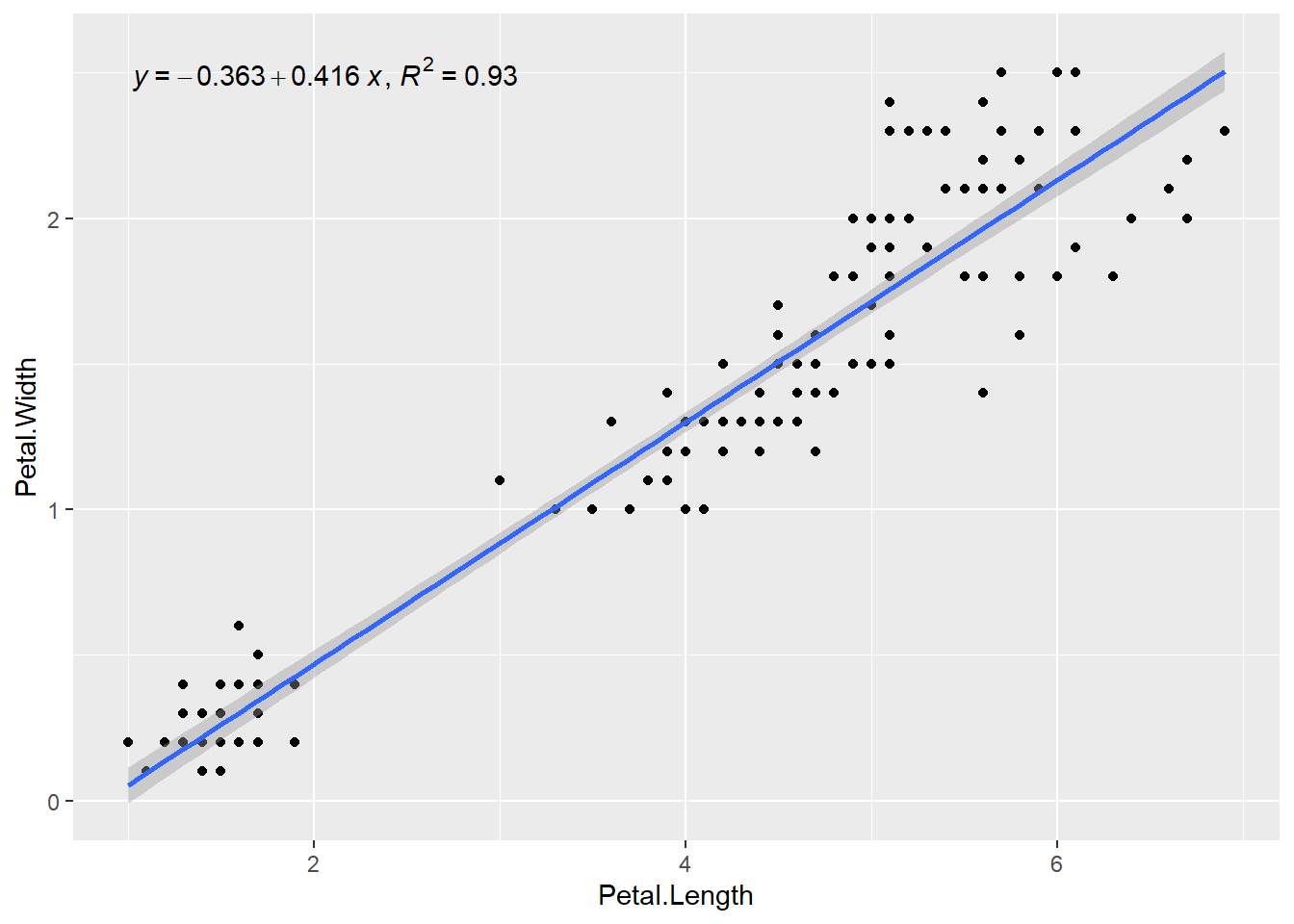
Figura 8.19: Relação entre o comprimento e largura de flores de espécies de Iris. Neste gráfico existe uma linha de tendência linear ajustada por geom_smooth.

Neste mesmo exemplo, é possível ajustar uma linha para cada espécie de Iris, mapeando as espécies para a cor.

ggplot(iris, aes(x = Petal.Length, y = Petal.Width, color = Species)) +
  geom_point() +
  stat_poly_line(formula = y ~ x) +
  stat_poly_eq(mapping = use_label("eq", "R2"), formula = y ~ x)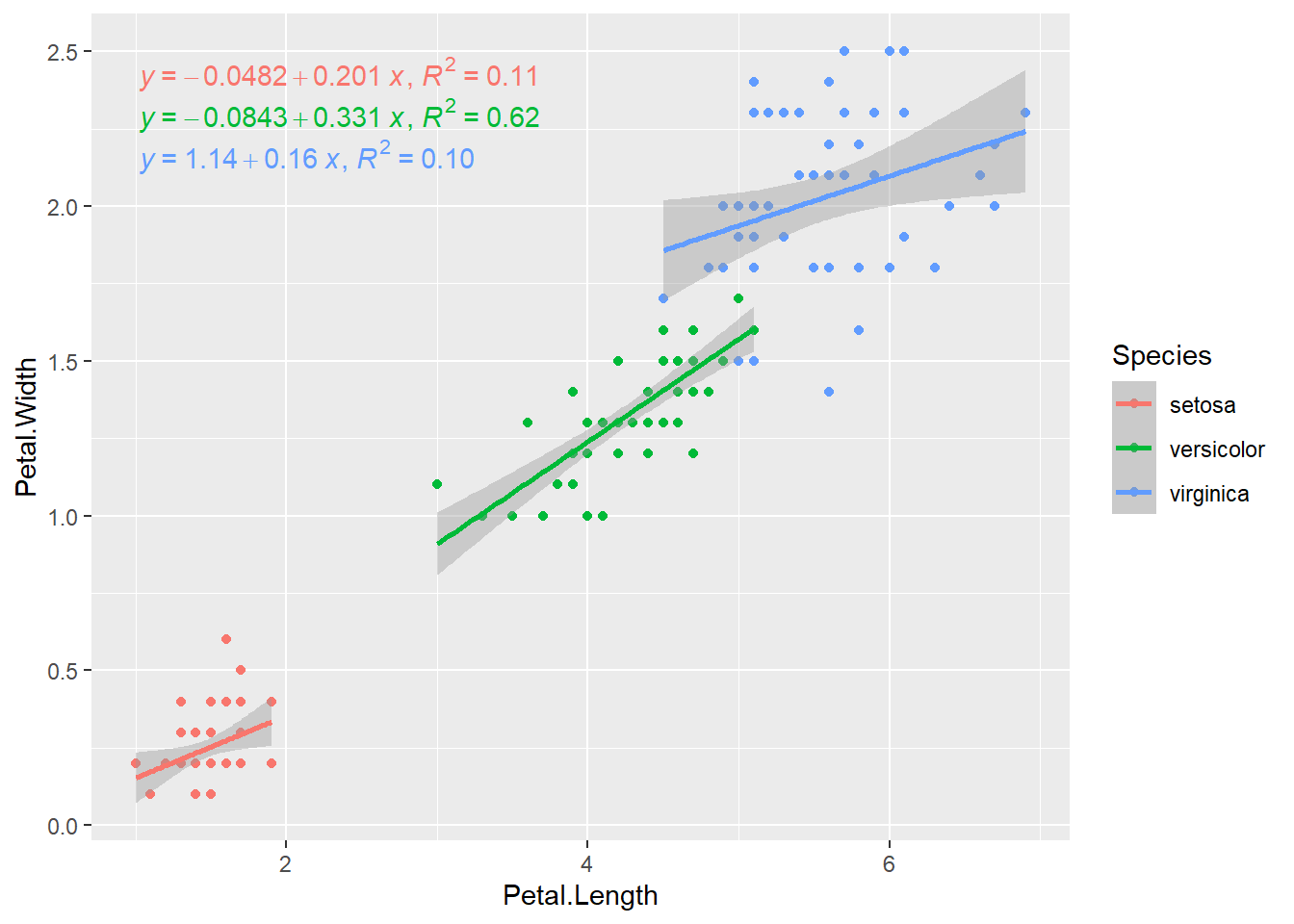
Figura 8.20: Relação entre o comprimento e largura de flores de espécies de Iris. As linhas de tendência são ajustadas para cada espécie que foram mapeadas para color.

8.4 Gráficos para distribuição

Uma distribuição de frequência é uma forma de resumir uma quantidade de dados distribuídos em classes ou intervalos. A frequência é o número de observações que pertencem a cada classe.

Nesta seção, serão apresentados vários tipos de gráficos utilizados para esta finalidade.

8.4.1 Histograma

O histograma é um tipo especial do gráfico de barras. No histograma, a largura de cada barra representa uma classe, e a altura das barras representa a frequência ou proporção dos valores contidos em cada classe. Via de regra, as barras do histograma devem ser apresentadas sem espaço entre elas. A geometria para a construção do histograma é geom_histogram.

Vamos exemplificar com a população de mogno africano descrito na Seção A.1.

ggplot(mogno, aes(x = dap)) +
  geom_histogram()
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.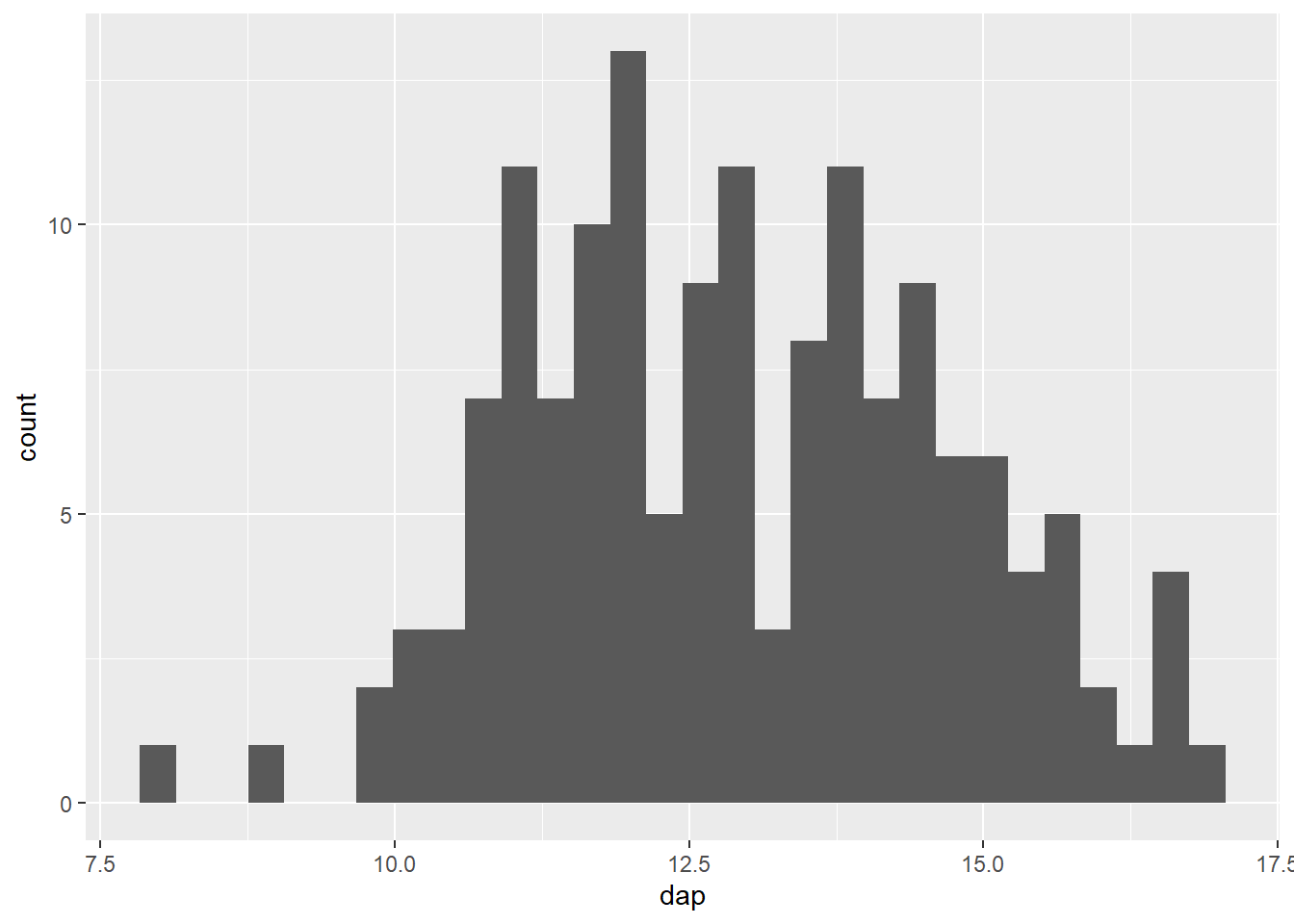
Figura 8.21: Histograma da distribuição de frequência do DAP, em centímetros, de árvores de de Mogno Africano.

A cor padrão do histograma do ggplot dificulta a separação das classes. É possível aprimorar este aspecto definindo uma cor para o contorno das barras.

ggplot(mogno, aes(x = dap)) +
  geom_histogram(color = "black")
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.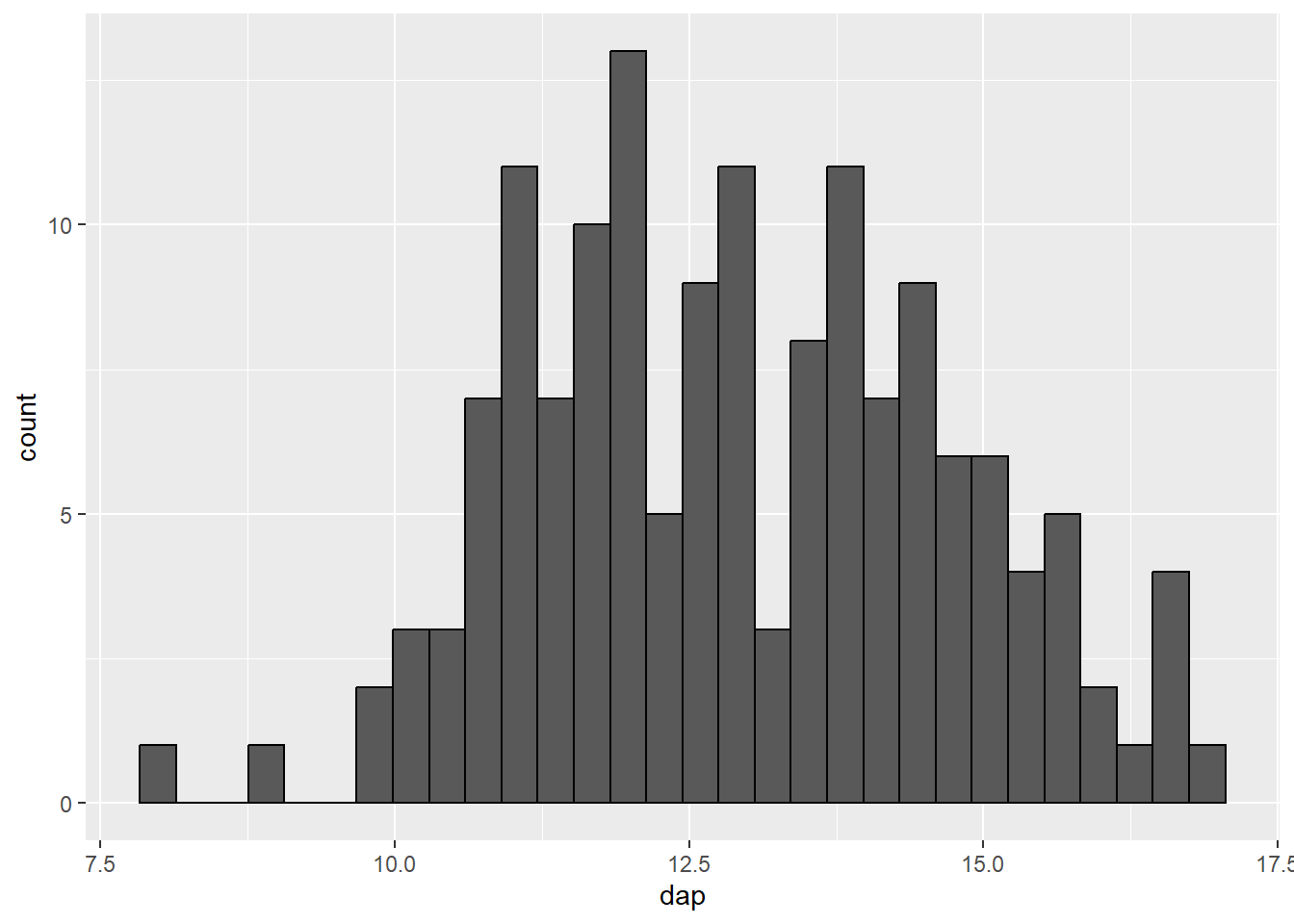
Figura 8.22: Histograma da distribuição de frequência do DAP, em centímetros, de árvores de de Mogno Africano. Foi definida uma cor para o contorno das barras (color = 'black') afim de melhorar a visualização destas.

Por padrão, o histograma feito com o ggplot é dividido em 30 classes (bins = 30. Este é um valor aleatório e não serve para a maioria dos casos. 3 Para alterar a quantidade de classes representada, há duas opções:

  1. Determinar o número de classes diretamente, modificando o argumento bins.
  2. Determinar a dimensão das classes, modificando o argumento binwidth.
ff_plot <- ggplot(mogno, aes(x = dap))
ff_plot + geom_histogram(bins = 20, color = "black")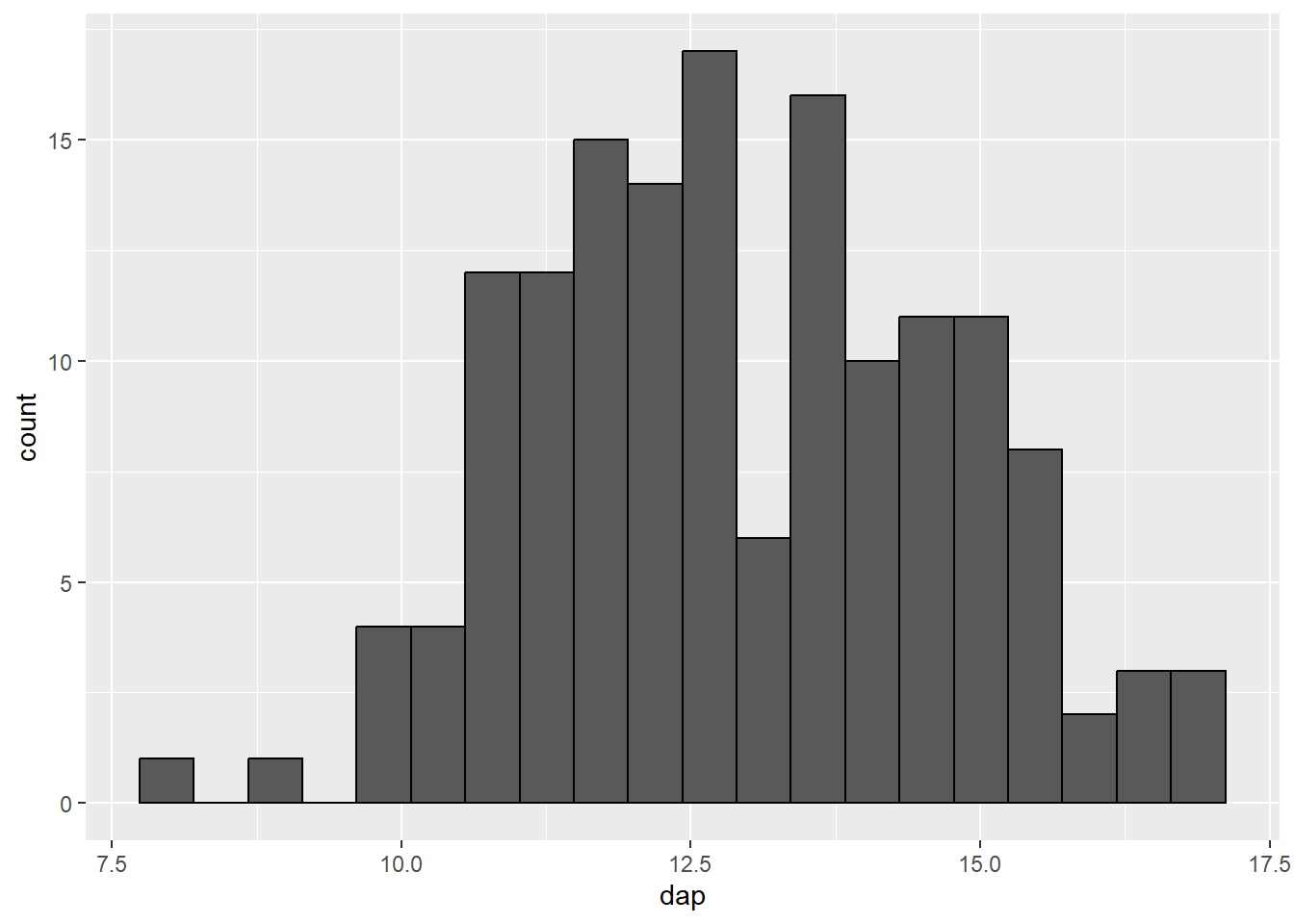
Figura 8.23: Histograma da distribuição de frequência do DAP, em centímetros, de árvores de de Mogno Africano. Este histograma foi contruído com 20 classes (bins = 20). 
ff_plot + geom_histogram(bins = 10, color = "black")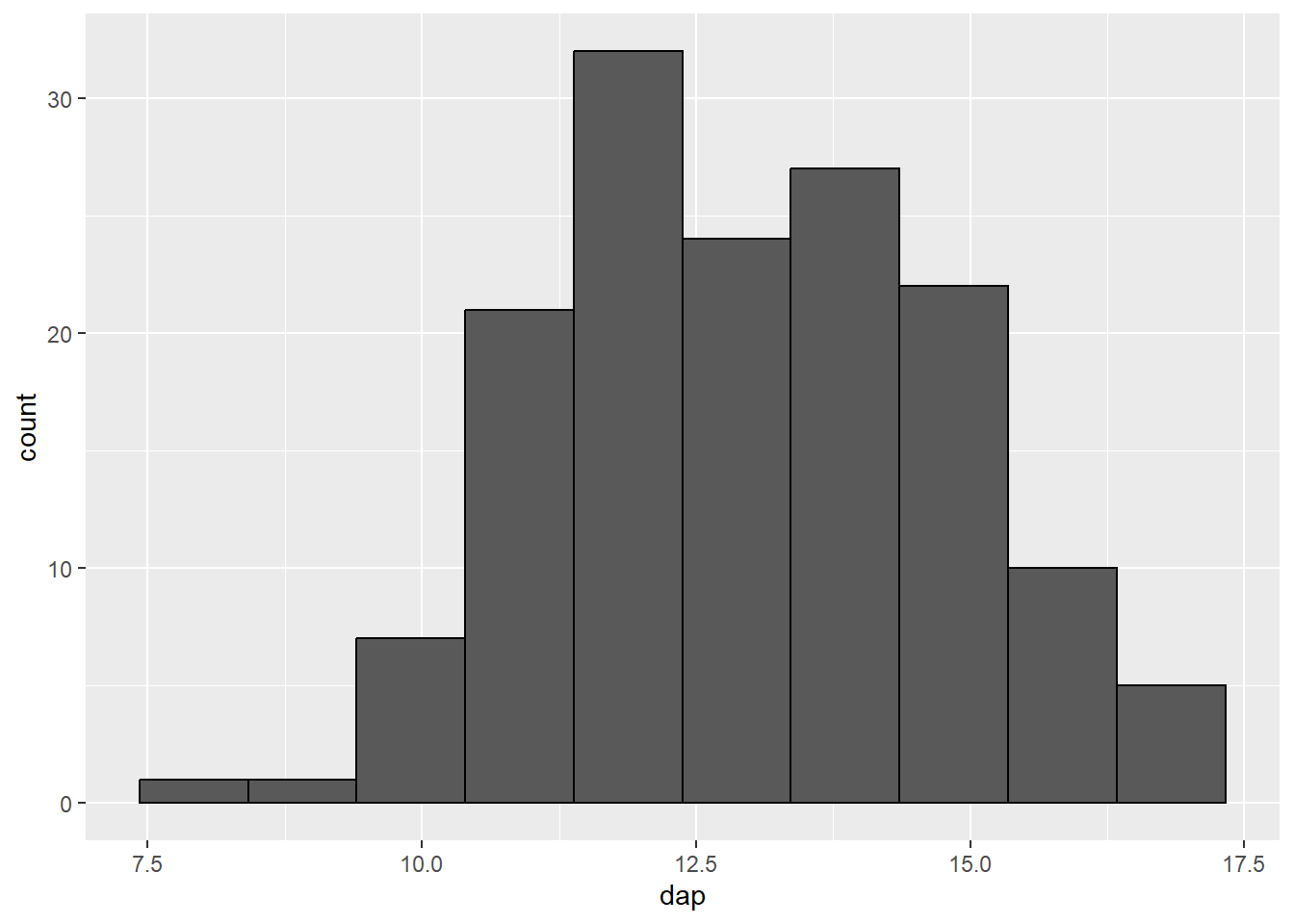
Figura 8.24: Histograma da distribuição de frequência do DAP, em centímetros, de árvores de de Mogno Africano. Este histograma foi contruído com 10 classes (bins = 10). 
ff_plot + geom_histogram(binwidth = 0.5, color = "black")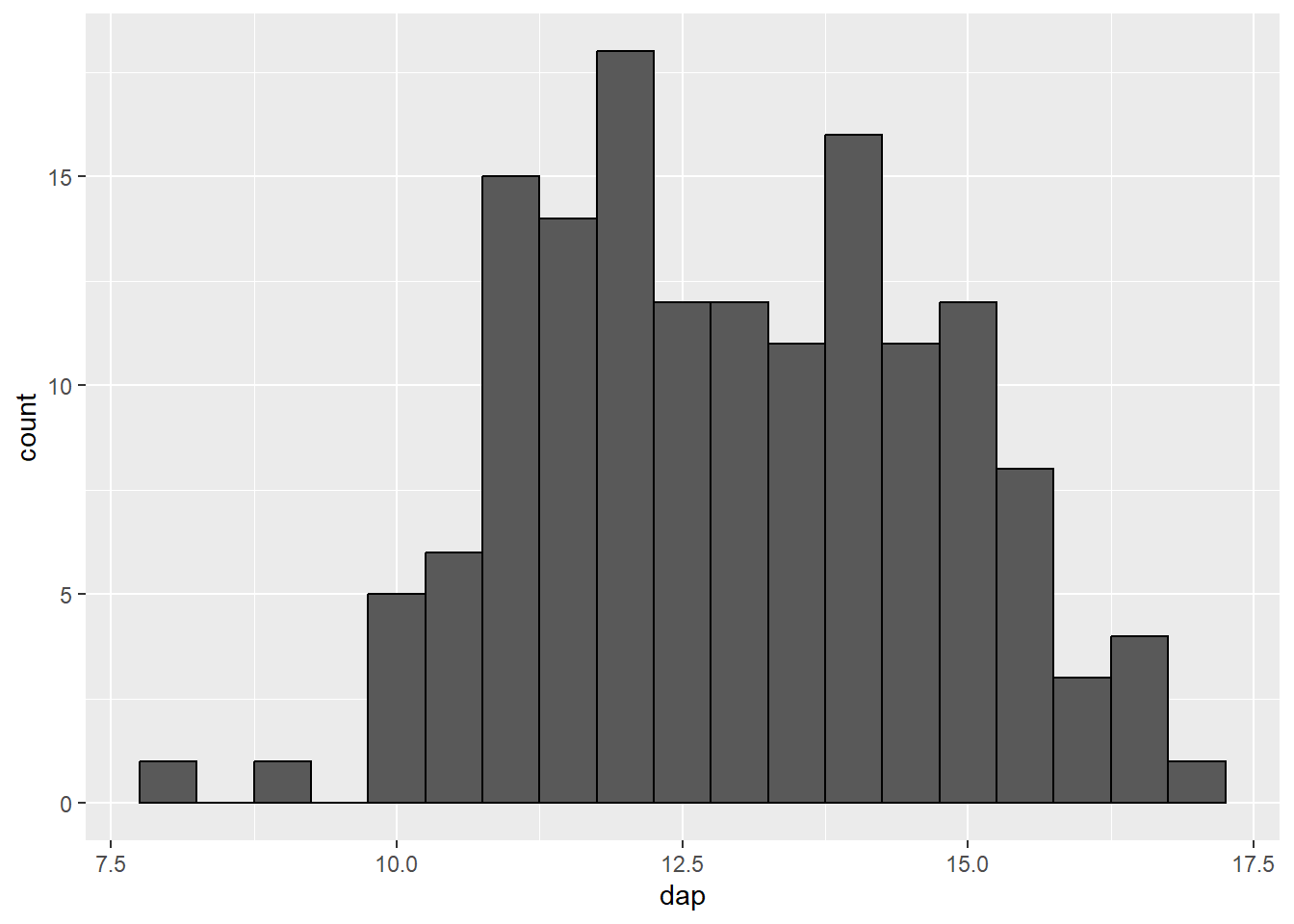
Figura 8.25: HistogrHistograma da distribuição de frequência do DAP, em centímetros, de árvores de de Mogno Africano. Este histograma foi contruído com o intervalo das classes igual a 0,5 cm (binwidth = 0.5). 
ff_plot + geom_histogram(binwidth = 0.1, color = "black")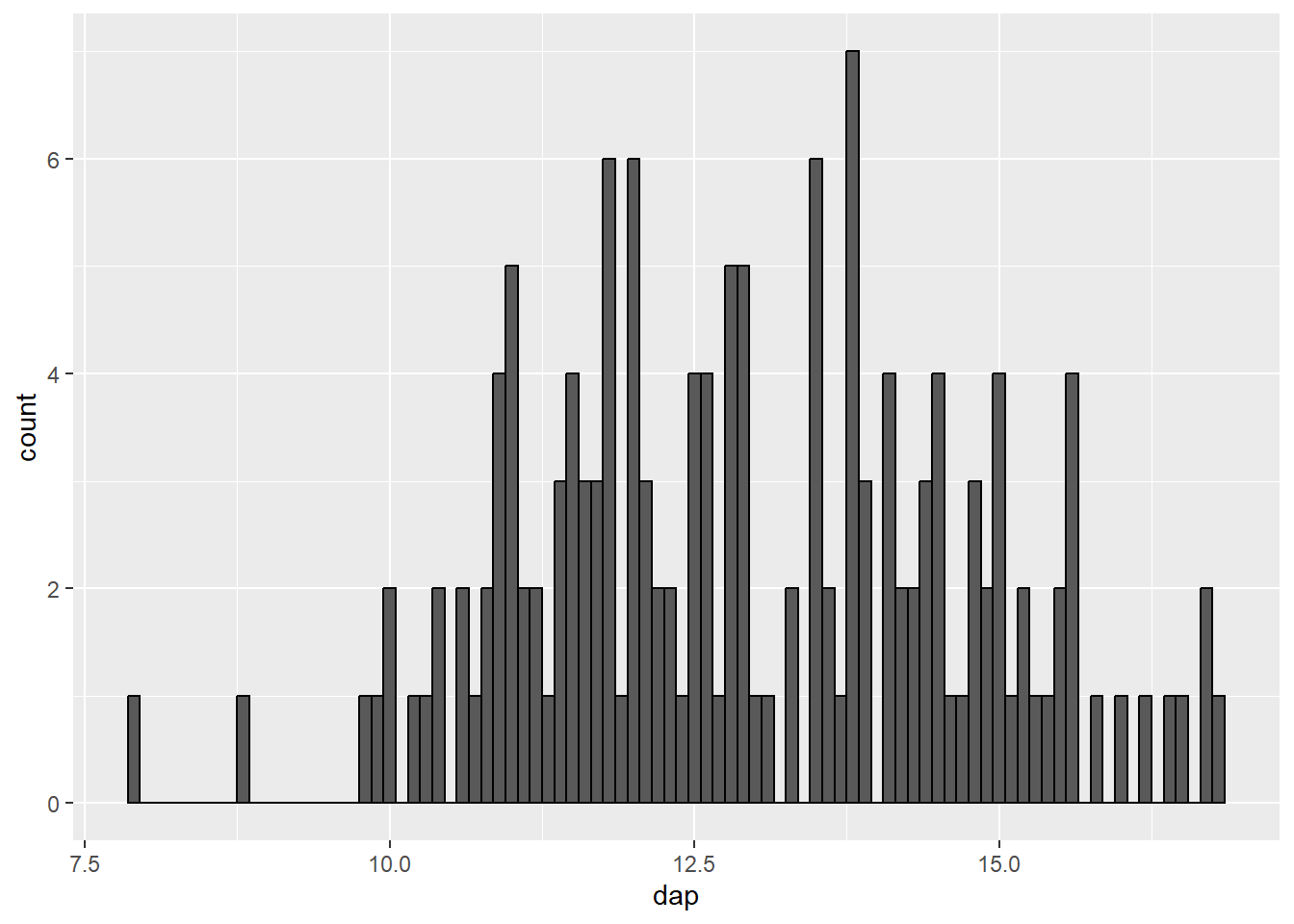
Figura 8.26: Histograma da distribuição de frequência do DAP, em centímetros, de árvores de de Mogno Africano. Este histograma foi contruído com o intervalo das classes igual a 0,1 cm (binwidth = 0.1).

8.4.2 Gráfico de densidade da distribuição

O gráfico de densidade da distribuição é uma versão suavizada do histograma. Para isso, este gráfico utiliza uma linha no lugar de barras (compare com a Figura Figura 8.22).

ggplot(mogno, aes(x = dap)) +
  geom_density()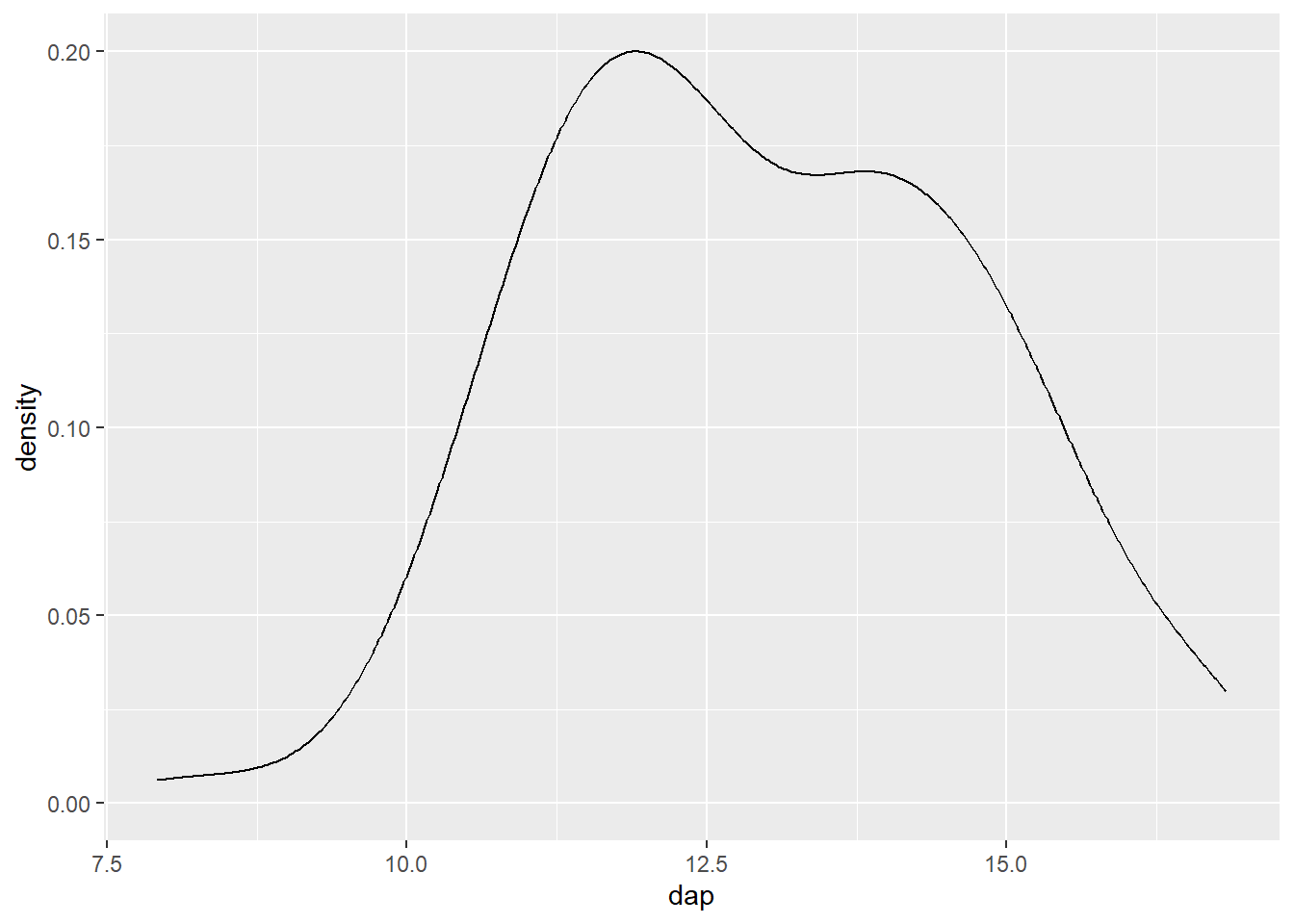
Figura 8.27: Densidade da distribuição do DAP, em centímetros, de árvores de de Mogno Africano.

Uma forma popular de apresentar este gráfico é preenchendo a área abaixo da linha. Isto é possível ajustando o argumento fill.

ggplot(mogno, aes(x = dap)) +
  geom_density(fill = "green", alpha = 0.5)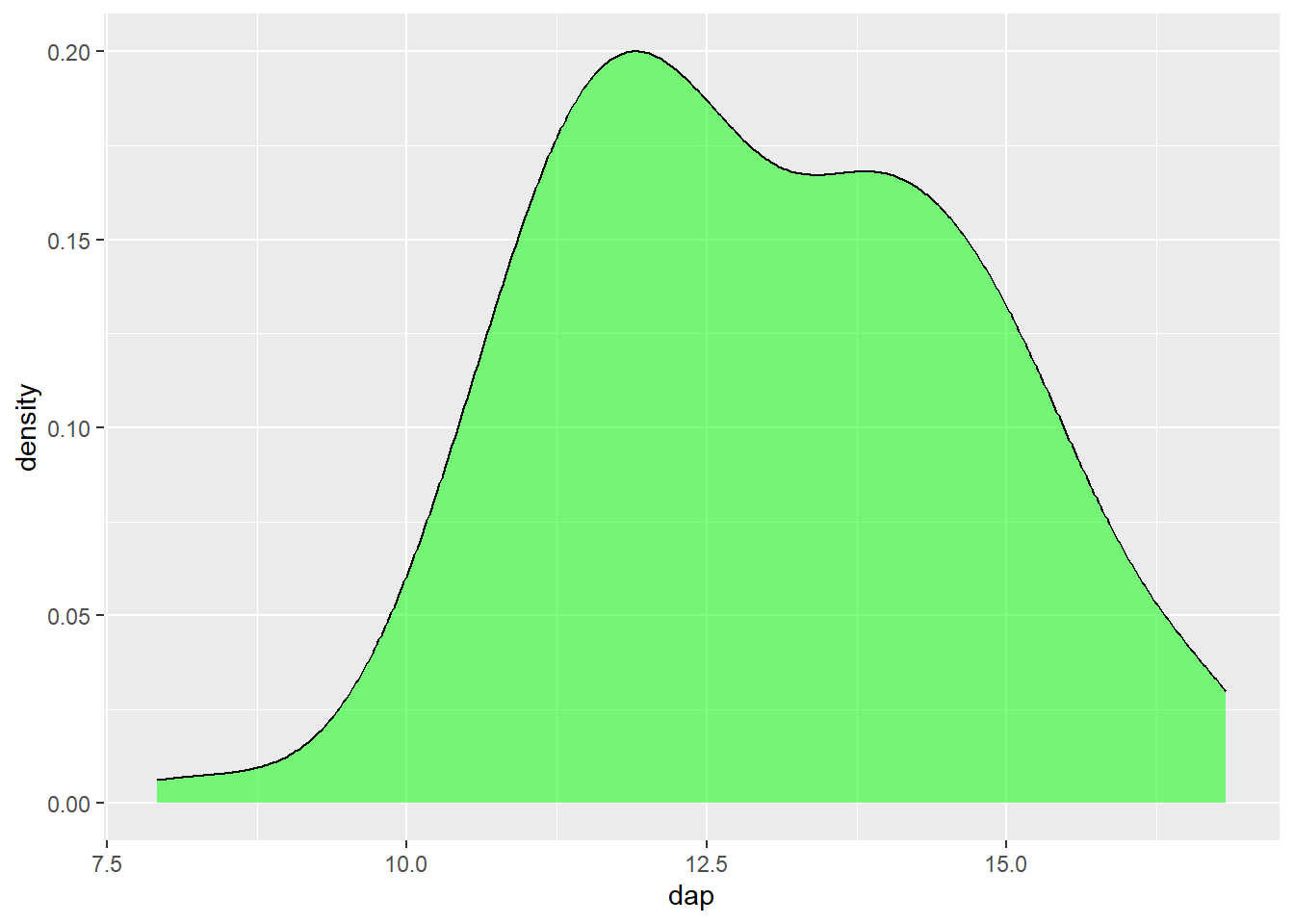
Figura 8.28: Densidade da distribuição do DAP, em centímetros, de árvores de de Mogno Africano. Ao ajustar o argumento fill é adicionada uma área preenchida abaixo da curva.

8.4.3 Box Plot

O Box plot, também conhecido como diagrama de caixa, representa uma distribuição por meio do resumo de cinco números:

  1. Limite inferior
  2. Primeiro quartil
  3. Mediana
  4. Terceiro quartil
  5. Limite superior

A figura abaixo mostra como estes valores formam o gráfico Box plot. A “caixa” (box) tem como limites o 1° e 3° quartis, medida que também é conhecida como Amplitude Interquartil (AIQ). Neste intervalo estão presentes 50% das observações. A linha dentro da caixa representa a mediana. Os “bigodes” (whiskers) se estendem até uma medida predeterminada, que pode ser:

  1. O mínimo e o máximo entre todos os valores;
  2. Os valores mais próximos a um limite inferior e um limite superior calculados por: \(L_i=Q_1-c \times AIQ\) e \(L_s=Q_3+c \times AIQ\), em que AIQ é a amplitude interquartil e c é um coeficiente cujo valor padrão é 1,5 4.

Os valores discrepantes, mais extremos que os limites, são plotados como pontos individuais.

Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.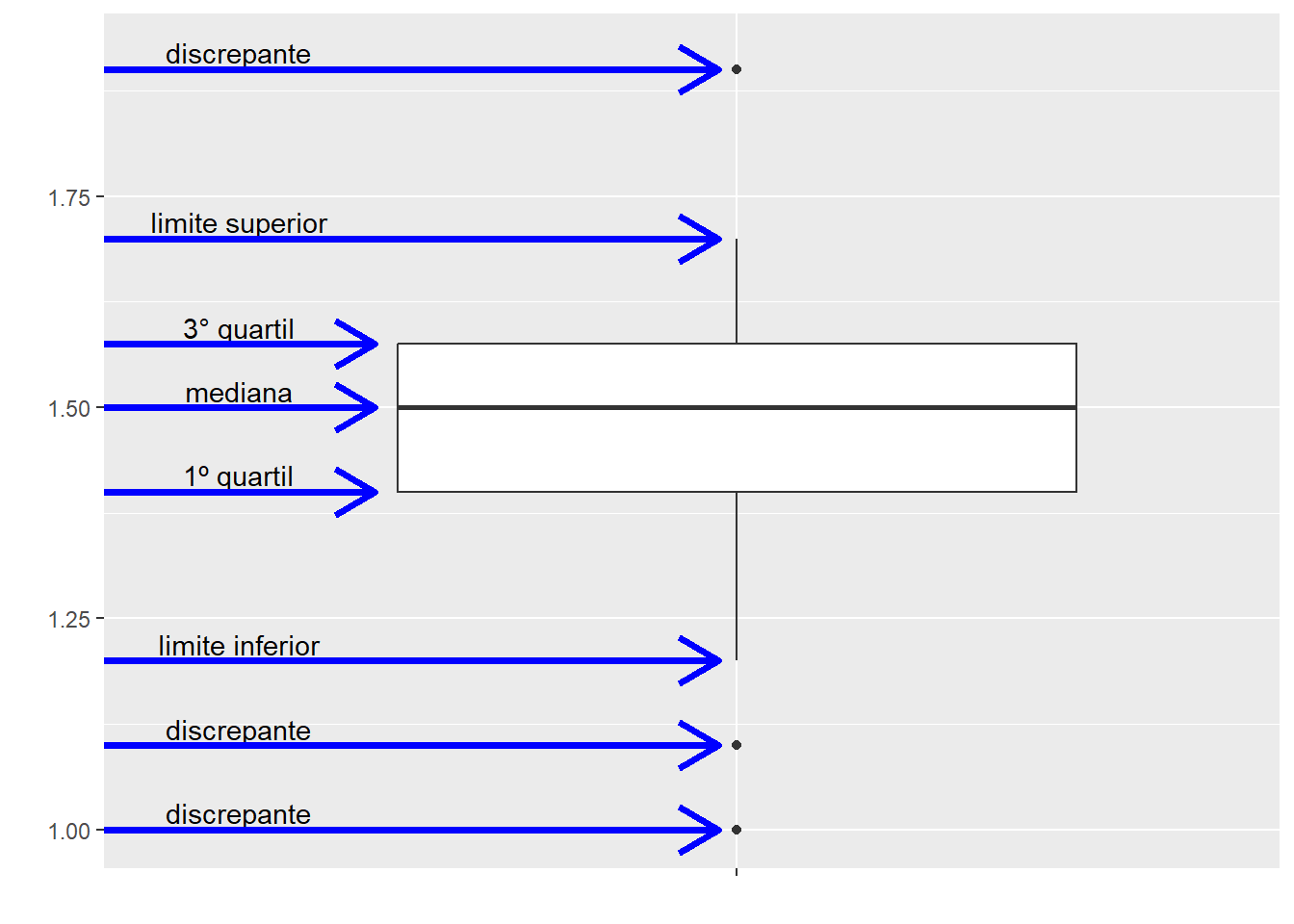

O Box plot utiliza a geometria geom_boxplot. A direção do gráfico (horizontal ou vertical) é ajustada mapeando a variável para o eixo x ou y

ggplot(mogno, aes(y = dap)) +
  geom_boxplot()
Figura 8.29: Box plot do tempo de espera entre erupções do gêiser Old Faithful. Mapear a variável para o eixo y resulta no boxplot vertical. 
ggplot(mogno, aes(x = dap)) +
  geom_boxplot()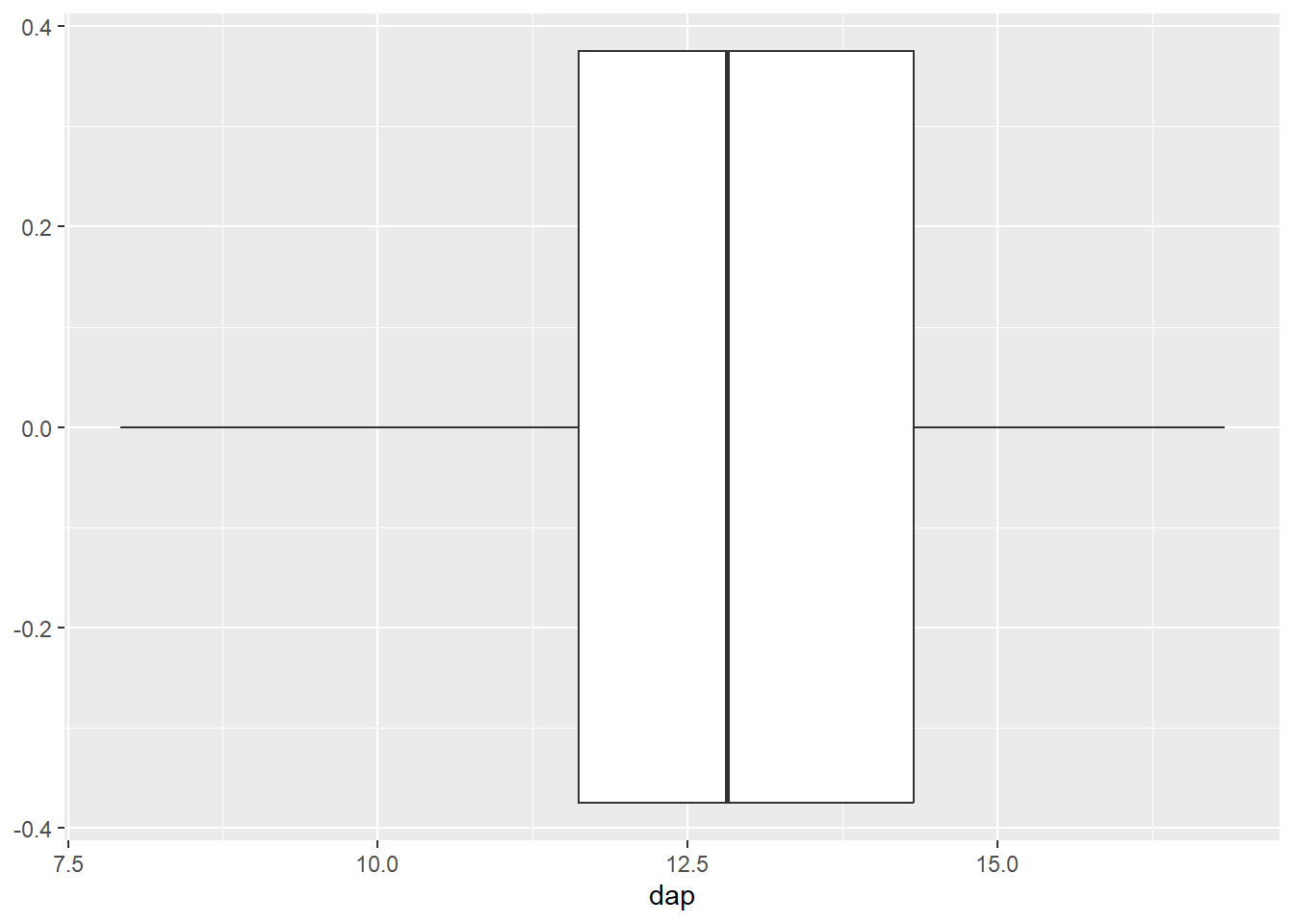
Figura 8.30: Box plot do tempo de espera entre erupções do gêiser Old Faithful. Mapear a variável para o eixo y resulta no boxplot horizontal.

Uma utilização bastante comum do Box plot é para comparar diferentes grupos. Para isso, plotamos o Boxplot para cada grupo dentro do mesmo gráfico. Vejamos este exemplo com os dados descritos em Seção A.7.

ggplot(algas, aes(x = riacho, y = biomassa)) +
  geom_boxplot()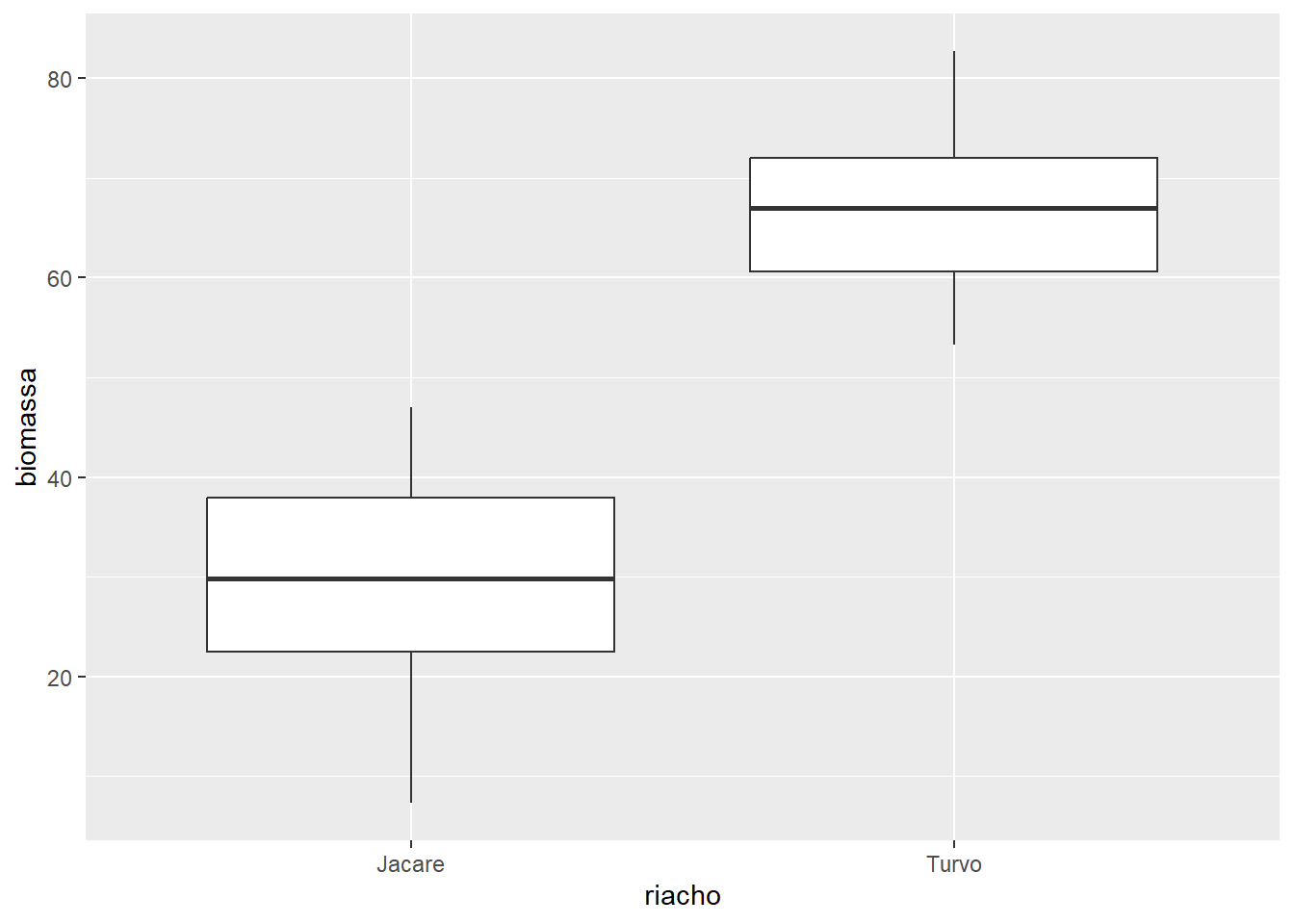
Figura 8.31: Biomassa de algas em dois riachos com diferentes níveis de poluição. O Box plot é uma excelente alternativa para a comparação entre diferentes classes.

O argumento coef ajusta o comprimentos dos bigodes como um múltiplo da AIQ. Por padrão, seu valor é de 1,5. Para que os bigodes se estendam até os valores máximos/mínimos, modificamos o argumento coef para NULL. Outros valores numéricos são possíveis para coef.

ggplot(algas, aes(x = riacho, y = biomassa)) +
  geom_boxplot(coef = NULL)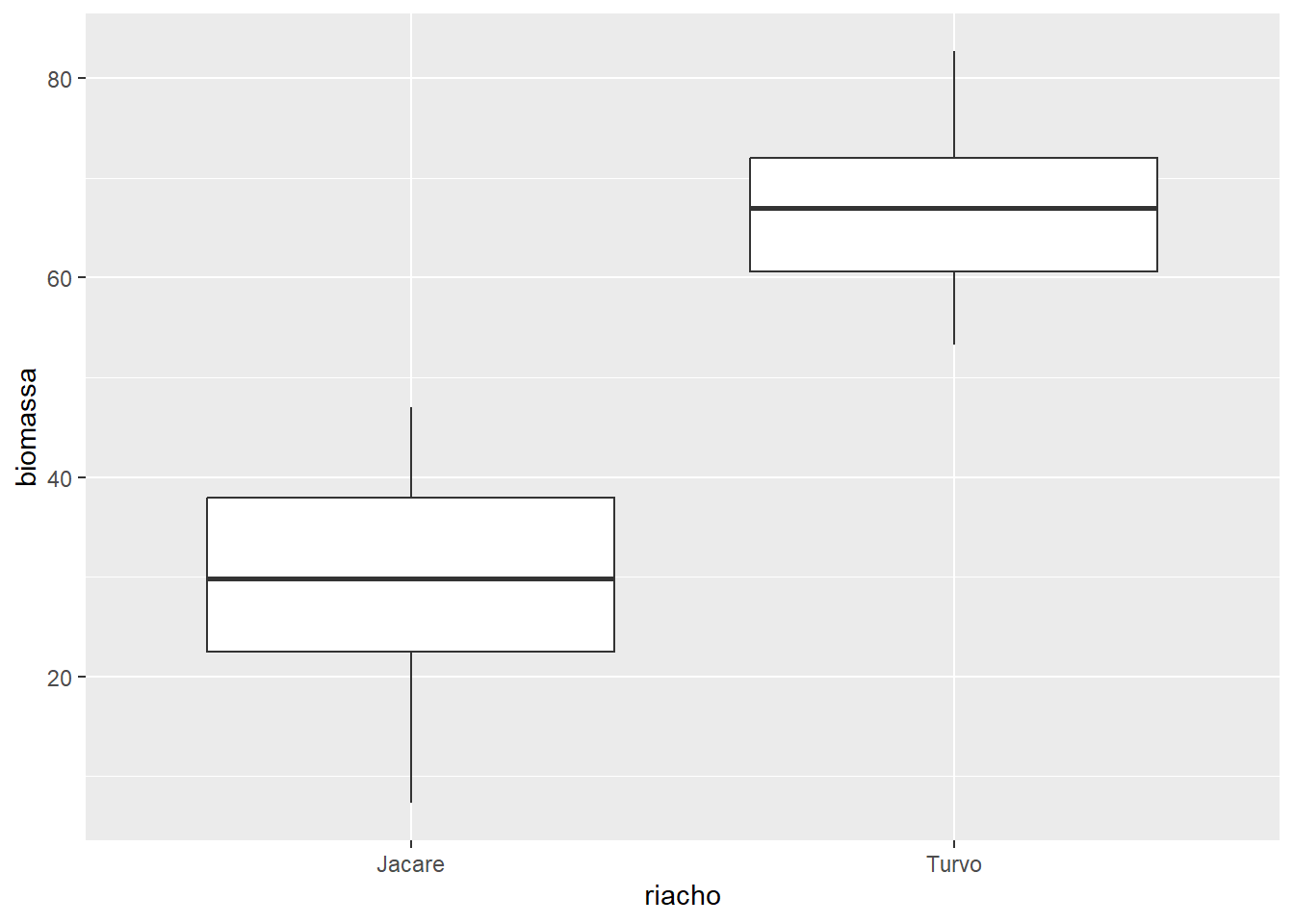
Figura 8.32: de algas em dois riachos com diferentes níveis de poluição. O comprimento dos bigodes alcança os valores mais extremos com o argumento coef = NULL. 
ggplot(algas, aes(x = riacho, y = biomassa)) +
  geom_boxplot(coef = 2.0)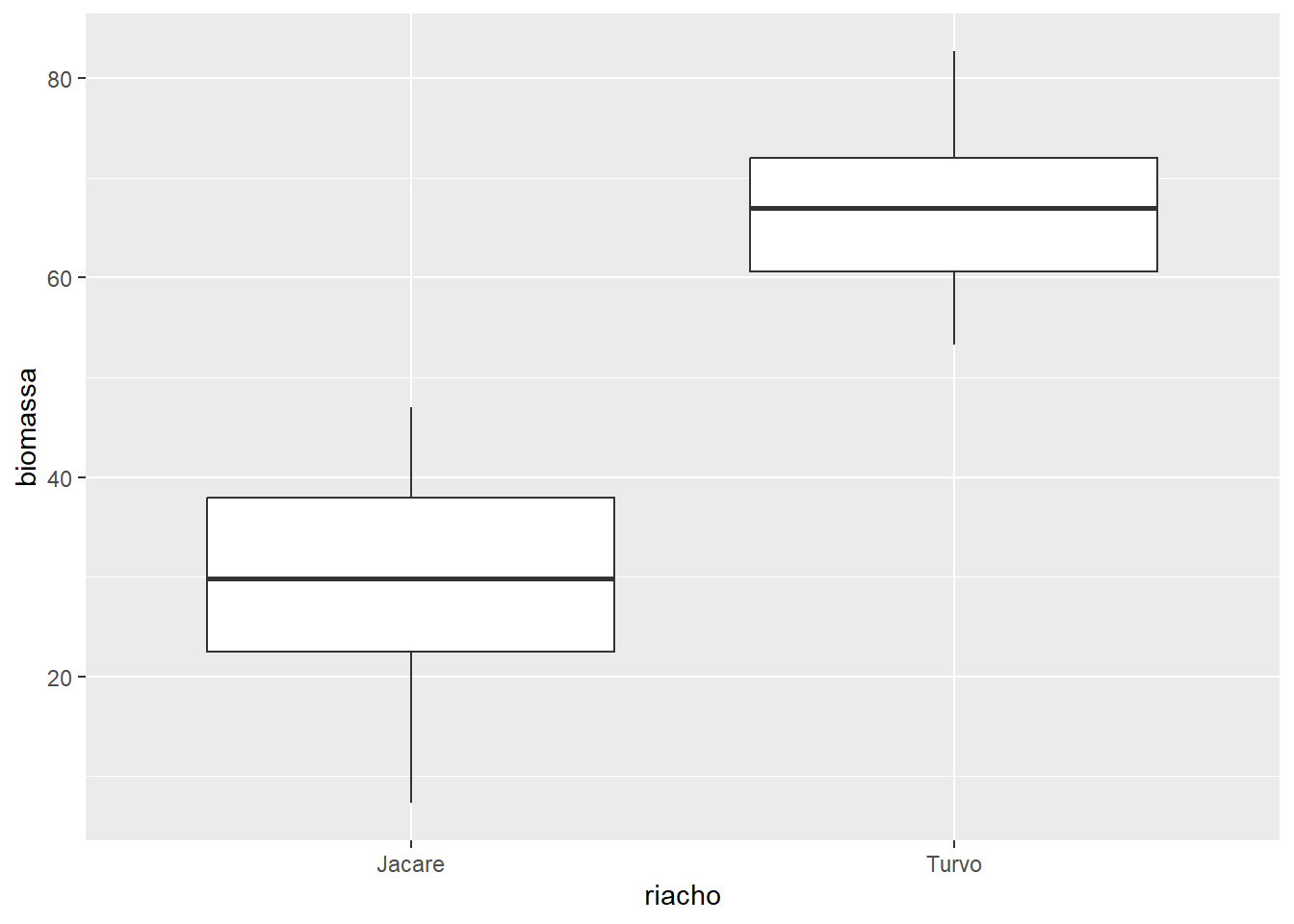
Figura 8.33: de algas em dois riachos com diferentes níveis de poluição. O argumento coef = 2.0 ajusta o comprimento dos bigodes para 2 vezes a AIQ. 
ggplot(algas, aes(x = riacho, y = biomassa)) +
  geom_boxplot(coef = 1.0)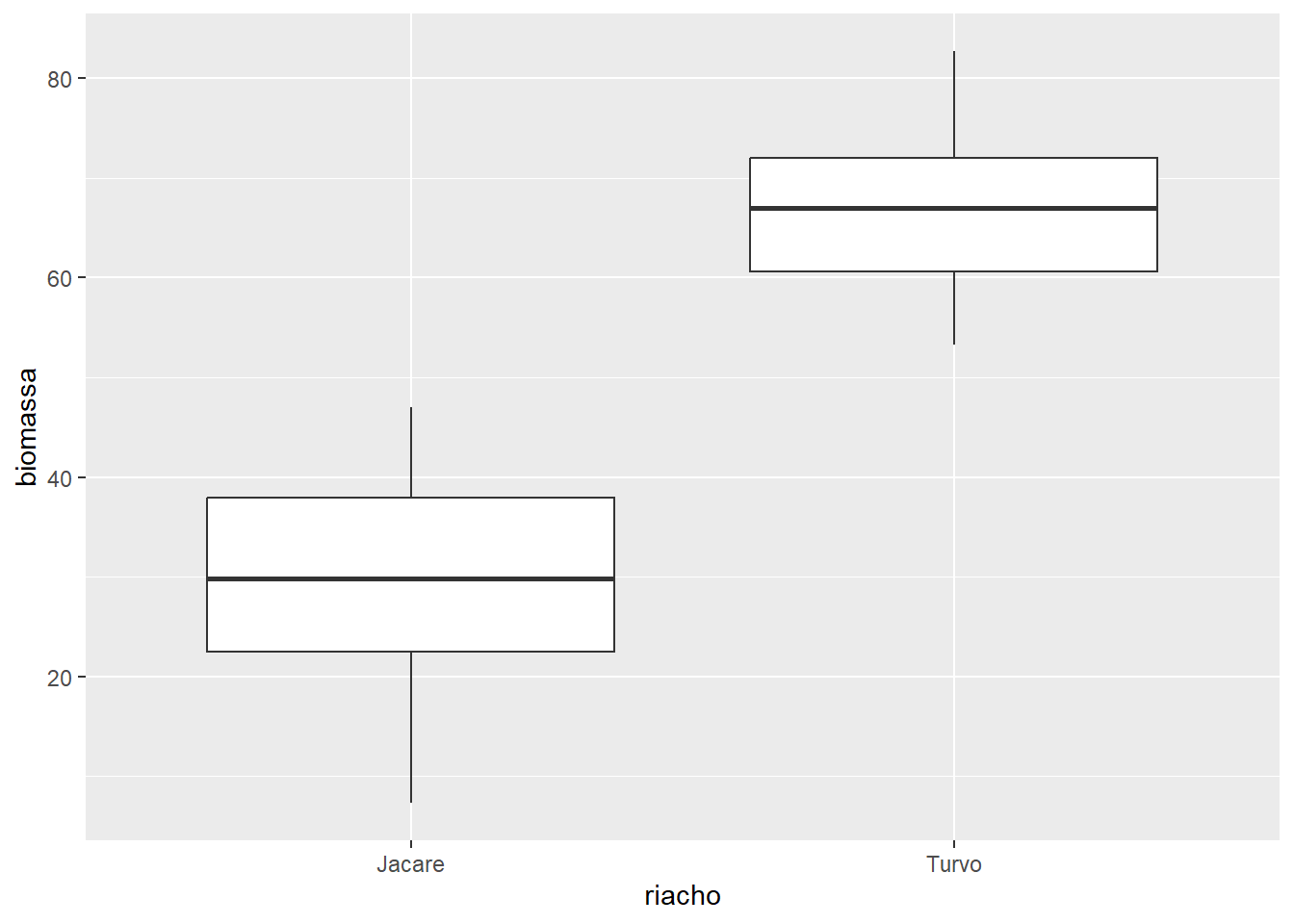
Figura 8.34: de algas em dois riachos com diferentes níveis de poluição. O argumento coef = 1.0 ajusta o comprimento dos bigodes para 1 vez a AIQ.

É possível adicionar uma marca para a média ao Boxplot. Para isso, utilizamos stat_summary para calcular a média e ajustamos um formato para a marca. O argumento shape=23 adiciona um losango (diamante), já que esse formato é bastante comum na representaçao da média.

ggplot(algas, aes(x = riacho, y = biomassa)) +
  geom_boxplot() +
  stat_summary(fun = "mean", shape = 23)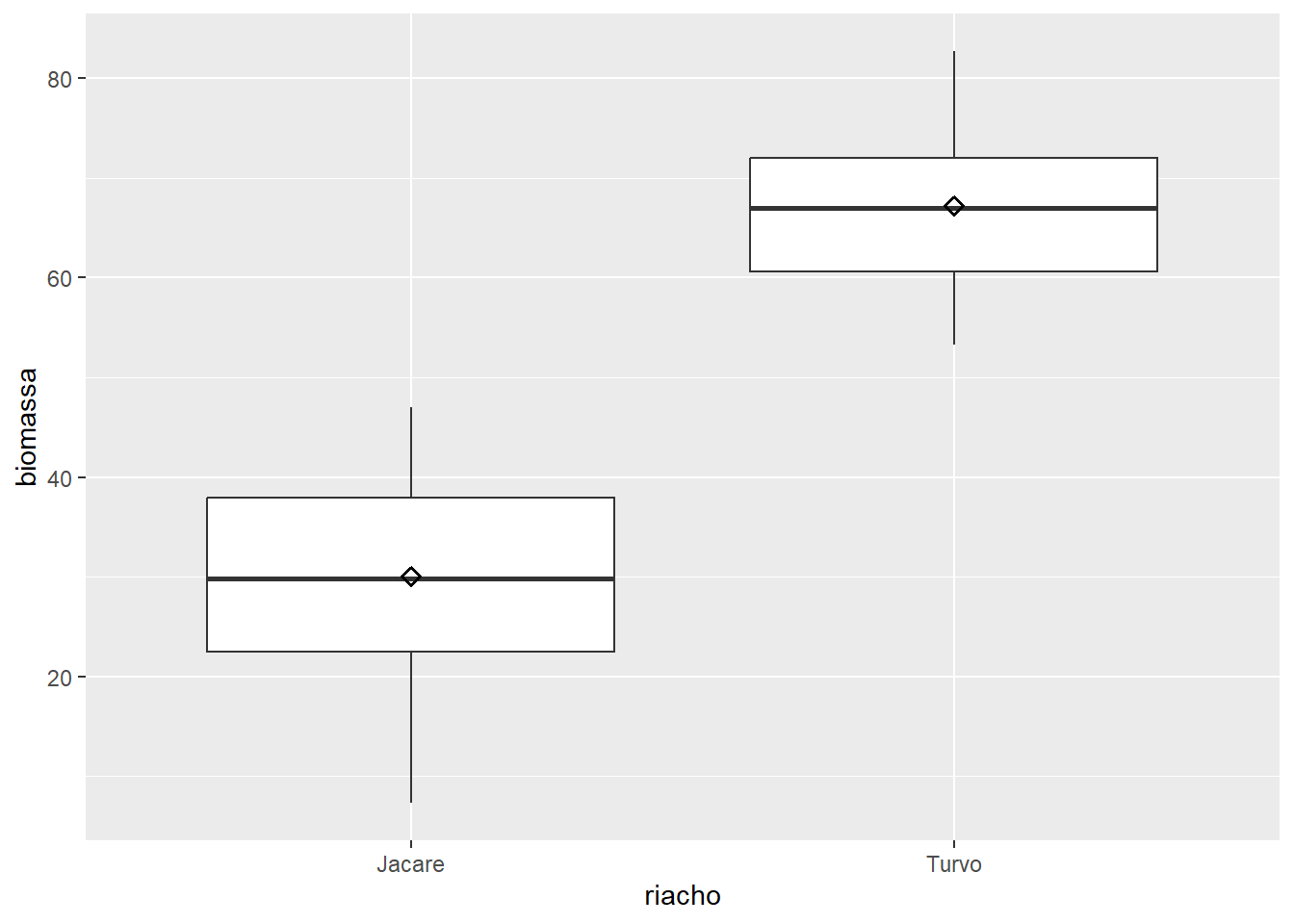
Figura 8.35: Consumo de combustível na rodovia segundo a classe dos automóveis. Uma marca em forma de losango foi adicionada para representar a média dos valores.

8.5 Gráficos interativos

O pacote plotly 5 permite a criação de gráficos interativos para a web.

pacman::p_load("plotly") # Carrega o pacote plotly

p <- ggplot(iris, aes(x = Petal.Length, y = Petal.Width, color = Species)) +
  geom_point()
plotly::ggplotly(p)

8.6 Gráficos animados

O pacote gganimate permite adicionar animações aos gráficos gerados com o ggplot.

pacman::p_load("gganimate", "gapminder") # Carrega os pacotes


p <- gapminder %>%
  group_by(continent, year) %>%
  summarise(median_lifeExp = median(lifeExp)) %>%
  ggplot(
    aes(x = year, y = median_lifeExp, group = continent, color = continent)
  ) +
  geom_line() +
  scale_color_viridis_d() +
  theme(legend.position = "top")
`summarise()` has grouped output by 'continent'. You can override using the
`.groups` argument.
p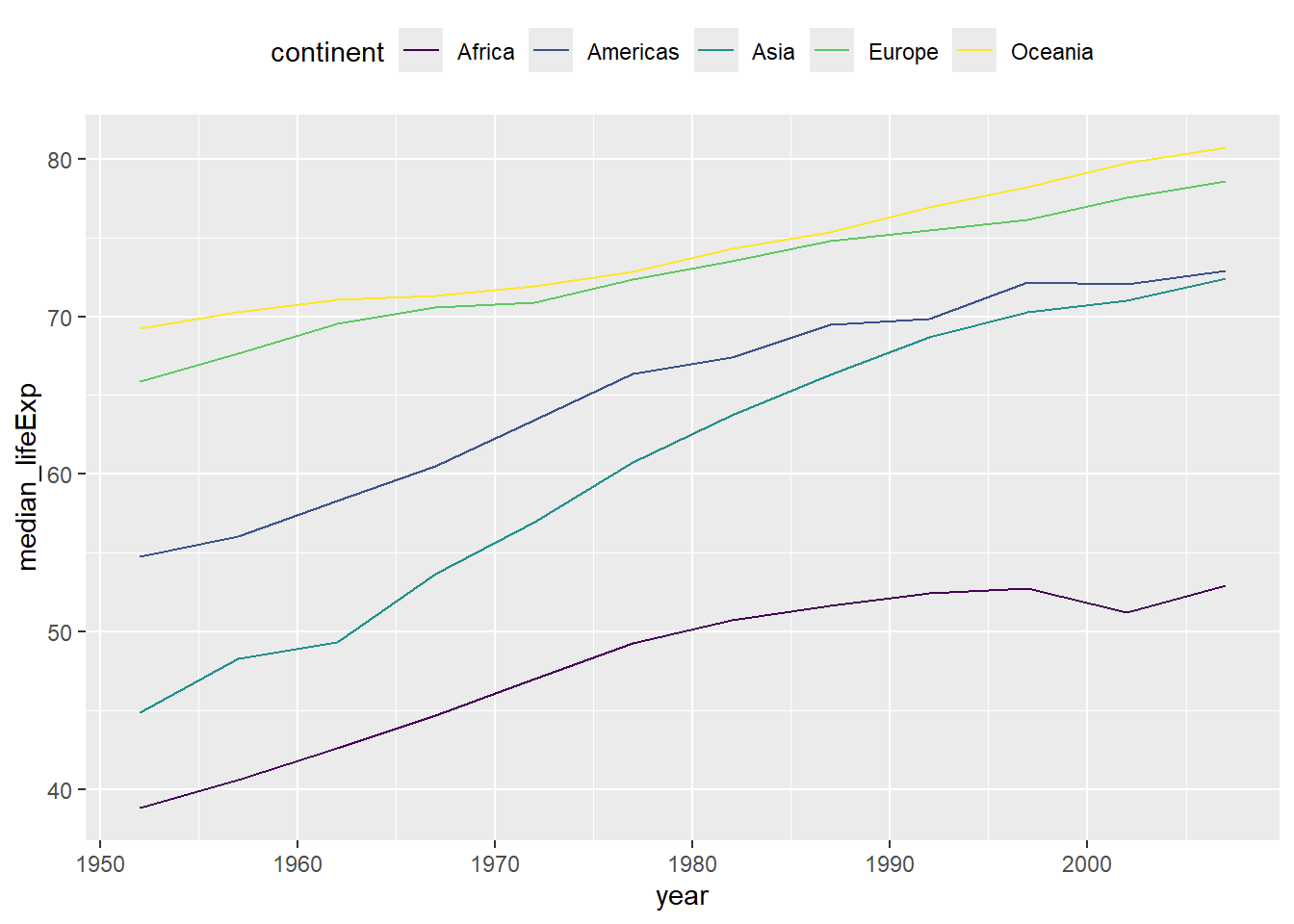

p +
  geom_point() +
  gganimate::transition_reveal(year)
`geom_line()`: Each group consists of only one observation.
ℹ Do you need to adjust the group aesthetic?
`geom_line()`: Each group consists of only one observation.
ℹ Do you need to adjust the group aesthetic?

  1. também conhecido como gráfico de dispersão↩︎

  2. Uma variável numérica contínua pode ser representada desde que esteja dividida em classes.↩︎

  3. Na verdade, este valor padrão é uma tentativa de forçar o usuário a determinar um valor adequado para o seu histograma.↩︎

  4. O valor de c=1,5 é capaz de abranger cerca de 99% das observações para uma distribuição Normal↩︎

  5. É preciso instalar e carregar o pacote plotly com os comandos install.packages("plotly") e library(plotly)↩︎