| term | df | sumsq | meansq | statistic | p.value |
|---|---|---|---|---|---|
| manejo | 2 | 708.87 | 354.43 | 106.63 | <0.001 * |
| Residuals | 21 | 69.80 | 3.32 | ||
| *Estatisticamente significativo (nível de 5%) | |||||
16 Testes de acompanhamento (post-hoc)
16.1 Teste de Tukey (HSD - Honest Significant Difference)
Criado por John Tukey (1915–2000), o teste de Tukey é um dos testes post-hoc (ou de comparações múltiplas) mais utilizados após uma ANOVA significativa. Ele realiza todas as comparações par a par possíveis entre as médias populacionais dos tratamentos, controlando o nível de significância do conjunto de todas as comparações (a “taxa de erro para a família de comparações”).
Em vez de usar um valor crítico do teste t padrão para cada comparação, o teste de Tukey utiliza um valor crítico próprio (baseado na distribuição “Studentized Range”), que leva em conta o número de médias sendo comparadas e o número de observações, mantendo o nível de significância global desejado (geralmente \(\alpha = 0.05\)).
As hipóteses testadas para cada par de médias \(i\) e \(j\) são:
\(H_0: \mu_i = \mu_j\) (As médias das populações \(i\) e \(j\) são iguais)
\(H_1: \mu_i \neq \mu_j\) (As médias das populações \(i\) e \(j\) são diferentes)
Existem muitos outros testes de comparações múltiplas similares ao de Tukey. Se você for capaz de interpretar os resultados deste teste, entenderá facilmente os de muitos outros.
Exemplo 16.1 (Teste de Tukey - Cobertura do Solo e Infiltração) Voltando ao Exemplo 14.1, onde a ANOVA indicou um efeito significativo do tipo de manejo da cobertura do solo sobre a taxa de infiltração de água (\(p < 0,001\)). Agora, queremos saber quais tipos de manejo diferem entre si:
- O Solo Descoberto (SD) difere da Gramínea Nativa (GN)?
- O Solo Descoberto (SD) difere da Leguminosa Consorciada (LC)?
- A Leguminosa Consorciada (LC) difere da Gramínea Nativa (GN)?
Para inicar, vamos refazer a Análise de Variância:
cobertura <- readr::read_csv("cobertura.csv") # importar os dados
aov_cobertura <- lm(infiltracao ~ manejo, data = cobertura)
anova(aov_cobertura)Utilizaremos o pacote emmeans para calcular o teste de Tukey e o pacote multcomp para obter a apresentação com letras (Compact Letter Display - CLD).
# Carregar pacotes se ainda não estiverem carregados
pacman::p_load("emmeans", "multcomp", "multcompView")
# Calcular as médias marginais estimadas e aplicar o teste de Tukey
tk_manejo <- emmeans::emmeans(aov_cobertura, ~manejo, contr = "tukey")
# Contrastes (comparações par a par)
tk_manejo$contrasts contrast estimate SE df t.ratio p.value
GN - LC -3,16 0,912 21 -3,469 0,0062
GN - SD 9,62 0,912 21 10,550 0,0000
LC - SD 12,78 0,912 21 14,020 0,0000
P value adjustment: tukey method for comparing a family of 3 estimates # Intervalos de confiança para os contrastes
tk_manejo$contrasts |> confint() contrast estimate SE df lower.CL upper.CL
GN - LC -3,16 0,912 21 -5,46 -0,865
GN - SD 9,62 0,912 21 7,32 11,915
LC - SD 12,78 0,912 21 10,48 15,078
Confidence level used: 0,95
Conf-level adjustment: tukey method for comparing a family of 3 estimates # Médias marginais estimadas e Compact Letter Display (CLD)
## Ajustar 'Letters = letters' ou 'Letters = LETTERS' para minúsculas ou maiúsculas
## Ajustar decreasing = TRUE para letras decrescentes e decreasing = FALSE para crescentes
tk_manejo$emmeans |> multcomp::cld(Letters = letters, decreasing = TRUE) manejo emmean SE df lower.CL upper.CL .group
LC 17,82 0,645 21 16,5 19,16 a
GN 14,66 0,645 21 13,3 16,00 b
SD 5,04 0,645 21 3,7 6,38 c
Confidence level used: 0,95
P value adjustment: tukey method for comparing a family of 3 estimates
significance level used: alpha = 0,05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same. # Gráfico das médias com intervalo de confiança
tk_manejo$emmeans |> plot(comparisons = TRUE, CIs = TRUE)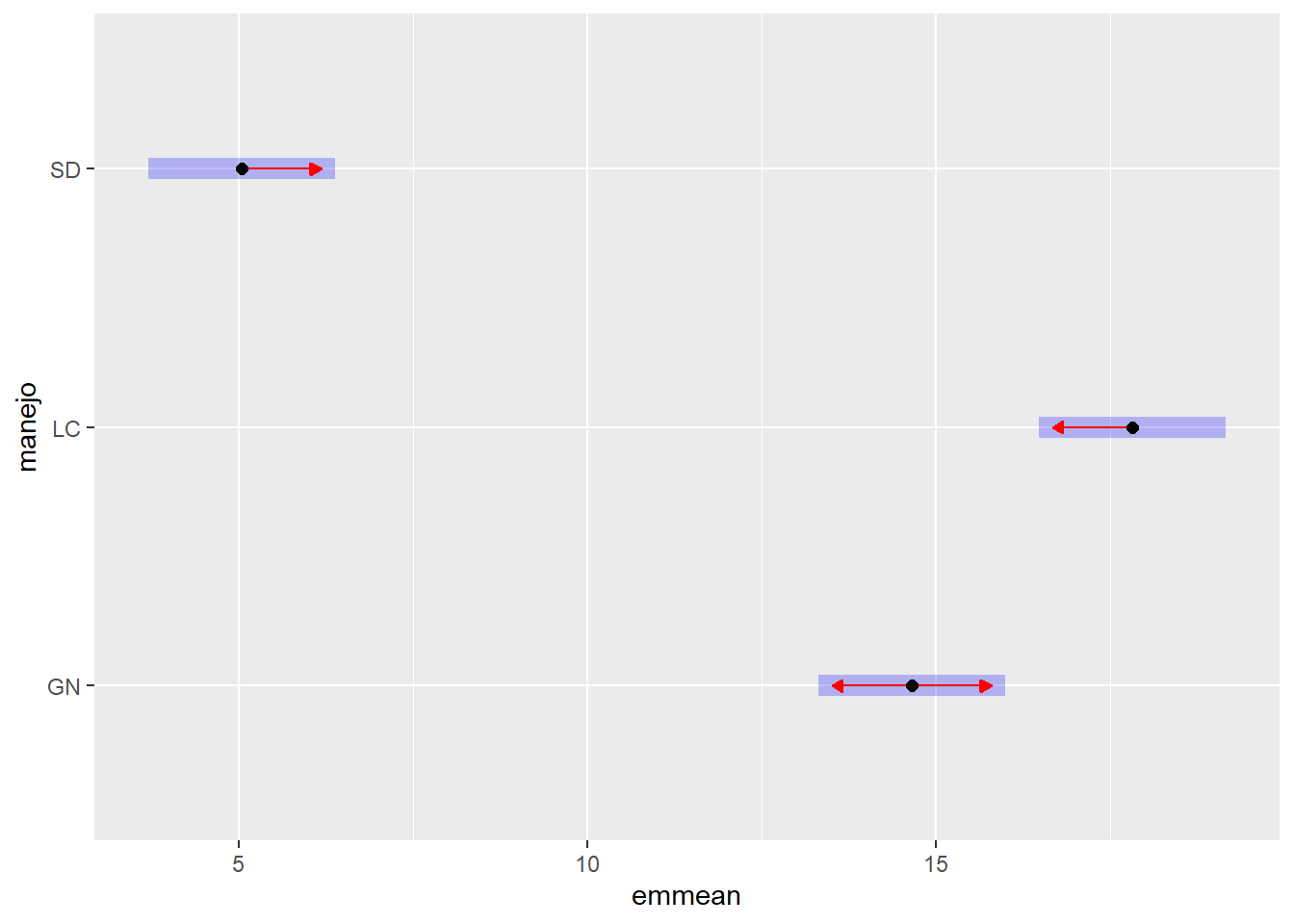
Apresentação e Interpretação dos Resultados:
Os resultados do teste de Tukey podem ser resumidos em uma tabela, usando as letras do CLD para indicar quais médias diferem significativamente.
Tabela X. Taxa média de infiltração de água (mm/hora) sob diferentes manejos de cobertura do solo.
| Manejo | Taxa de infiltração |
|---|---|
| LC | 17.82 a |
| GN | 14.66 b |
| SD | 5.04 c |
| Médias com a mesma letra não diferem significativamente (teste de Tukey, 0%) | |
Médias seguidas pela mesma letra na coluna não diferem significativamente entre si pelo teste de Tukey (p < 0,05).
Conclusão:
Com base nos resultados do teste de Tukey (p < 0,05):
- A Leguminosa Consorciada (LC) apresentou a maior taxa média de infiltração (17,82 mm/hora), sendo significativamente superior tanto à Gramínea Nativa (GN) quanto ao Solo Descoberto (SD).
- A Gramínea Nativa (GN) teve uma taxa média de infiltração (14,66 mm/hora) significativamente maior que o Solo Descoberto (SD).
- O Solo Descoberto (SD) apresentou a menor taxa média de infiltração (5,04 mm/hora), diferindo significativamente dos manejos com cobertura vegetal.
Portanto, todos os três tipos de manejo da cobertura do solo resultaram em taxas médias de infiltração de água estatisticamente diferentes entre si, com a ordem de eficácia (da maior para a menor infiltração) sendo: Leguminosa Consorciada > Gramínea Nativa > Solo Descoberto.
16.2 Teste de Dunnett
O teste de Dunnett é apropriado quando desejamos comparar especificamente vários tratamentos contra um grupo controle ou referência.
Vamos efetuar o teste com os dados do Exemplo 15.1.
Exemplo 16.2 (Teste de Dunnett) .
Refazendo a Análise de Variância:
shiitake <- readr::read_csv("shiitake.csv") # importar os dados
aov_shiitake <- lm(prod ~ subs + bloco, data = shiitake)
anova(aov_shiitake)| term | df | sumsq | meansq | statistic | p.value |
|---|---|---|---|---|---|
| subs | 5 | 1,131.19 | 226.24 | 30.27 | <0.001 * |
| bloco | 3 | 981.05 | 327.02 | 43.75 | <0.001 * |
| Residuals | 15 | 112.11 | 7.47 | ||
| *Estatisticamente significativo (nível de 5%) | |||||
# Carregar pacotes se ainda não estiverem carregados
pacman::p_load("emmeans")
# Calcular as médias marginais estimadas e aplicar o teste de Dunnett
dn_shiitake <- emmeans::emmeans(aov_shiitake, ~subs,
contr = "dunnett",
ref = which(names(table(shiitake$subs)) == "testemunha")
)
# Contrastes (comparações contra a testemunha)
dn_shiitake$contrasts contrast estimate SE df t.ratio p.value
S1 - testemunha 3,80 1,93 15 1,966 0,2336
S2 - testemunha -0,55 1,93 15 -0,285 0,9889
S3 - testemunha 13,91 1,93 15 7,196 0,0000
S4 - testemunha 3,17 1,93 15 1,639 0,3772
S5 - testemunha 17,36 1,93 15 8,978 0,0000
Results are averaged over the levels of: bloco
P value adjustment: dunnettx method for 5 tests # Intervalos de confiança para os contrastes
dn_shiitake$contrasts %>% confint() contrast estimate SE df lower.CL upper.CL
S1 - testemunha 3,80 1,93 15 -1,69 9,29
S2 - testemunha -0,55 1,93 15 -6,04 4,94
S3 - testemunha 13,91 1,93 15 8,42 19,40
S4 - testemunha 3,17 1,93 15 -2,32 8,65
S5 - testemunha 17,36 1,93 15 11,87 22,84
Results are averaged over the levels of: bloco
Confidence level used: 0,95
Conf-level adjustment: dunnettx method for 5 estimates # Médias marginais estimadas
dn_shiitake$emmeans subs emmean SE df lower.CL upper.CL
S1 28,4 1,37 15 25,5 31,3
S2 24,1 1,37 15 21,2 27,0
S3 38,5 1,37 15 35,6 41,5
S4 27,8 1,37 15 24,9 30,7
S5 42,0 1,37 15 39,1 44,9
testemunha 24,6 1,37 15 21,7 27,5
Results are averaged over the levels of: bloco
Confidence level used: 0,95 # Gráfico das médias com intervalo de confiança
dn_shiitake$emmeans %>% plot(comparisons = TRUE, CIs = TRUE)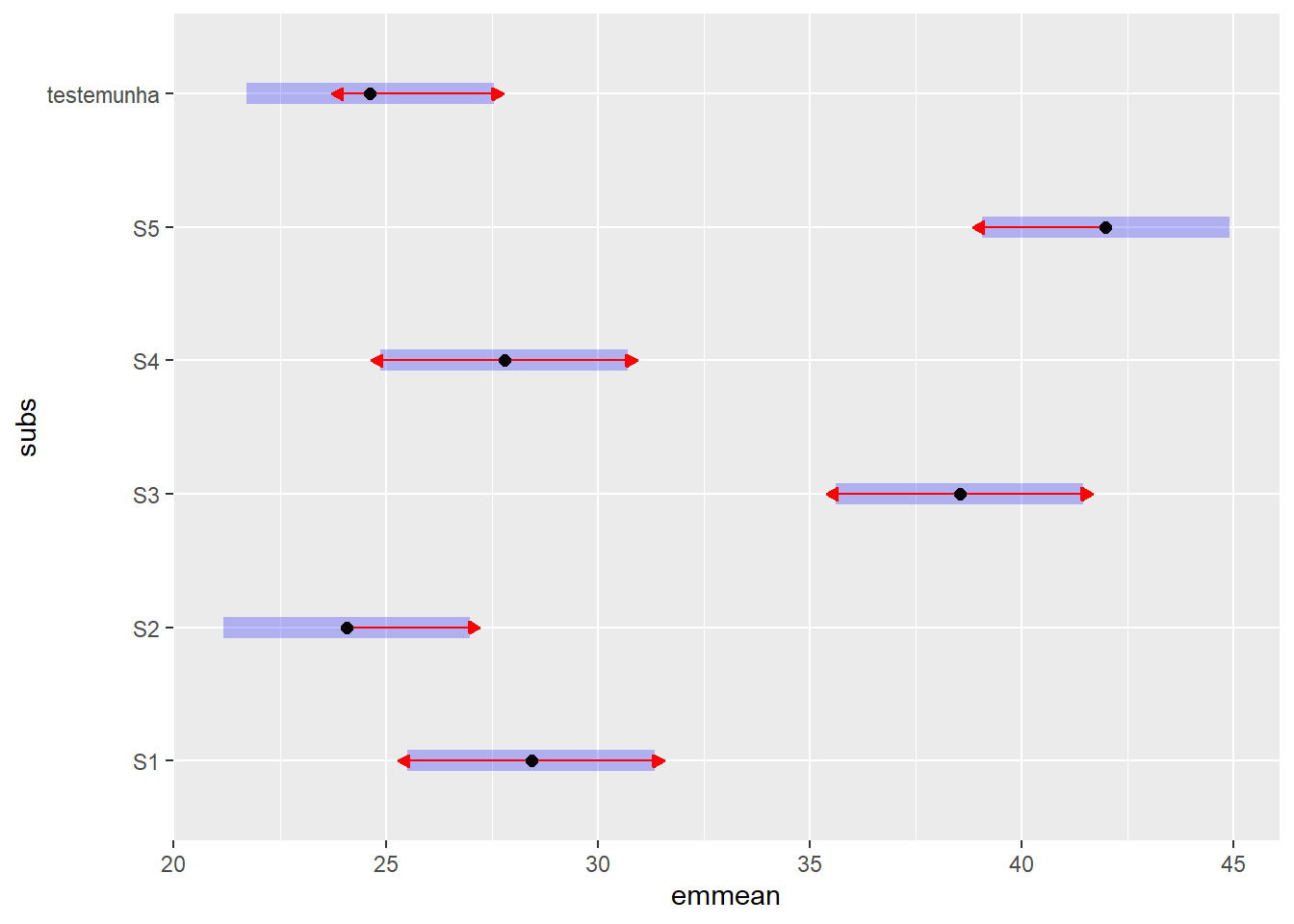
Uma tabela com os resultados do teste de Dunnett pode ser elaborada.
Tabela X. Produtividade média de cogumelos Shiitake (em kg/saca, ajustada pelos blocos) para diferentes substratos.
| Substratos | Produção de shiitake |
|---|---|
| S1 | 28.43 |
| S2 | 24.08 |
| S3 | 38.54 * |
| S4 | 27.80 |
| S5 | 41.99 * |
| testemunha | 24.63 |
| *Diferença significativa em relação ao controle (teste de Dunnett, 5%). | |
Médias seguidas por um asterisco diferem significativamente do tratamento testemunha pelo teste de Dunnett (p < 0,05).
Conclusão:
Os substratos S5 e S3 apresentaram uma produtividade média de shiitake significativamente superior à do substrato Testemunha.
Os substratos S1, S2 e S4 não apresentaram produtividades médias estatisticamente diferentes daquela observada para o substrato Testemunha.
Notavelmente, a produtividade do substrato S2 foi numericamente inferior à da testemunha, mas essa diferença não foi estatisticamente significativa.
16.3 Teste de Scott-Knott
O teste de Scott-Knott tem como objetivo agrupar as médias dos tratamentos em grupos homogêneos, ou seja, grupos cujas médias não apresentam diferenças estatísticas significativas entre si, minimizando a variação dentro dos grupos e maximizando-a entre eles, sem sobreposição.
Exemplo 16.3 (Teste de Scott-Knott - Resistência a ferrugem.) Um programa de melhoramento de soja está avaliando 12 linhagens experimentais (L1 a L12) quanto à sua resistência à ferrugem asiática. O experimento foi conduzido em casa de vegetação, sob condições controladas, com inoculação artificial do patógeno. Utilizou-se um delineamento em blocos casualizados com 5 repetições.
A variável resposta utilizada para avaliar a resistência foi a severidade da doença, medida como a porcentagem média de área foliar com sintomas da ferrugem asiática, 20 dias após a inoculação. Menores valores de severidade indicam maior resistência.
Os dados estão disponíveis no arquivo ferrugem.csv.
# Análise de Variância
aov_ferrugem <- lm(res ~ gen+bloco, data = ferrugem)
anova(aov_ferrugem)Analysis of Variance Table
Response: res
Df Sum Sq Mean Sq F value Pr(>F)
gen 11 662,90 60,263 25,503 1,536e-15 ***
bloco 4 149,16 37,290 15,781 4,399e-08 ***
Residuals 44 103,97 2,363
---
Signif. codes: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1# Teste de Scott-Knott
pacman::p_load("ScottKnott")
sk_ferrugem <- ScottKnott::SK(aov_ferrugem)List of 2
$ new.fact.lev:List of 1
..$ gen: chr [1:12] "LN_1" "LN_2" "LN_3" "LN_4" ...
$ grid.data :'data.frame': 12 obs. of 1 variable:
..$ gen: chr [1:12] "LN_1" "LN_2" "LN_3" "LN_4" ...sk_ferrugemResults
Means G1 G2 G3 G4
LN_11 33,04 a
LN_10 32,25 a
LN_12 31,92 a
LN_8 30,09 b
LN_9 29,91 b
LN_6 28,14 c
LN_7 27,51 c
LN_5 26,88 c
LN_4 26,80 c
LN_3 24,86 d
LN_1 23,46 d
LN_2 22,31 d
Sig.level
0,05
Statistics
lambda chisq dfchisq pvalue evmean dferror
Clus 1 48,20 19,0 10,5 8,8e-07 0,47 44
Clus 2 16,45 10,1 4,4 3,4e-03 0,47 44
Clus 3 1,83 7,2 2,6 5,4e-01 0,47 44
Clus 4 0,05 5,5 1,8 9,6e-01 0,47 44
Clus 5 34,65 12,8 6,1 5,7e-06 0,47 44
Clus 6 2,93 8,7 3,5 4,9e-01 0,47 44
Clus 7 6,96 7,2 2,6 5,5e-02 0,47 44
Clusters
################# Cluster 1 ################
{G1}: LN_11 LN_10 LN_12 LN_8 LN_9
{G2}: LN_6 LN_7 LN_5 LN_4 LN_3 LN_1 LN_2
################# Cluster 2 ################
{G1}: LN_11 LN_10 LN_12
{G2}: LN_8 LN_9
################# Cluster 3 ################
{G1}: LN_11
{G2}: LN_10 LN_12
################# Cluster 4 ################
{G1}: LN_8
{G2}: LN_9
################# Cluster 5 ################
{G1}: LN_6 LN_7 LN_5 LN_4
{G2}: LN_3 LN_1 LN_2
################# Cluster 6 ################
{G1}: LN_6 LN_7
{G2}: LN_5 LN_4
################# Cluster 7 ################
{G1}: LN_3
{G2}: LN_1 LN_2Os testes post-hoc podem ser executados com os scripts: