19 Correlação e Regressão

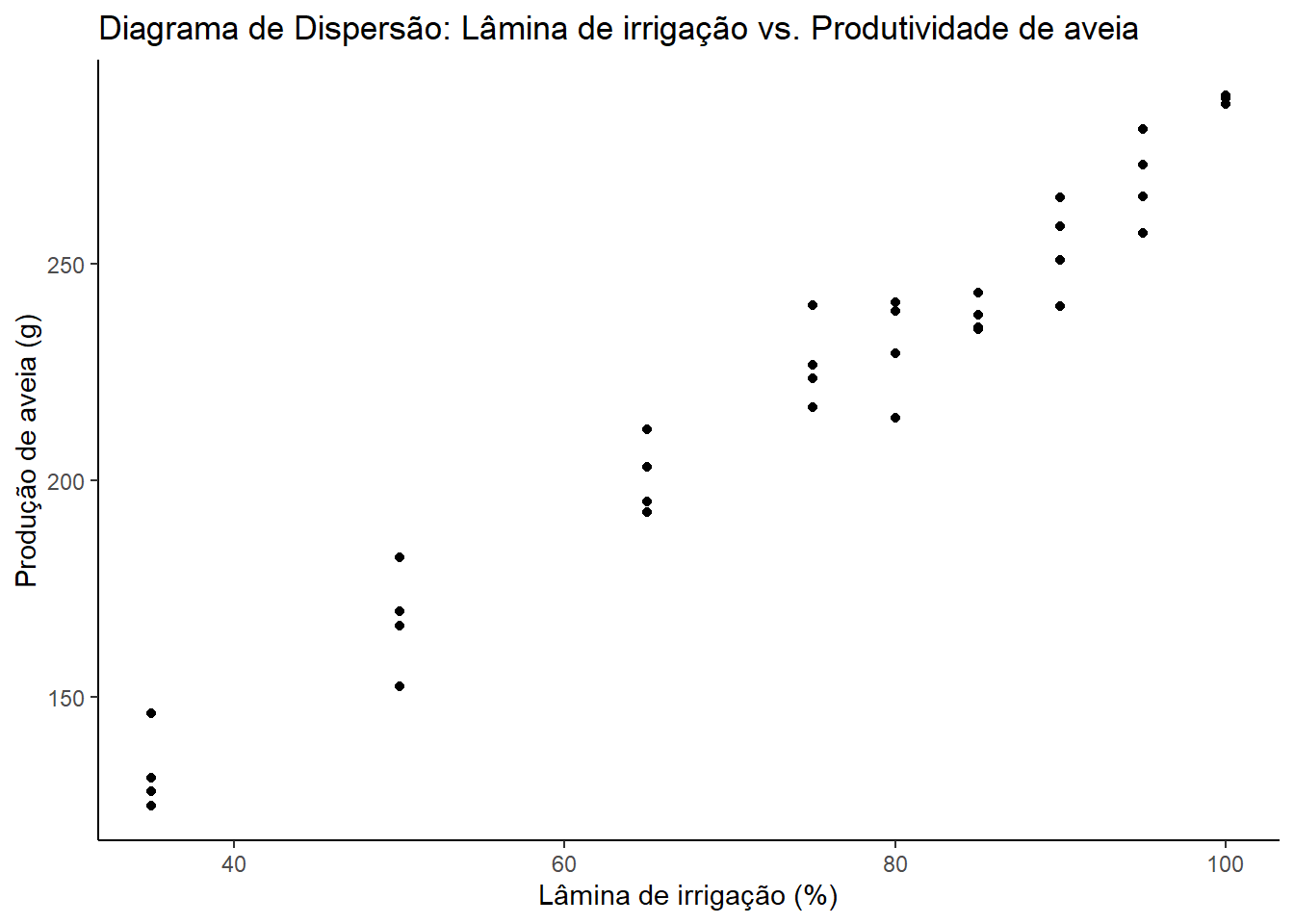
Muitos estudos investigam a relação entre duas ou mais variáveis quantitativas. É fundamental compreender que as relações estatísticas identificadas representam tendências gerais e não regras determinísticas, comportando exceções individuais. Por exemplo, embora uma maior aplicação de fertilizante nitrogenado possa, em média, aumentar a produtividade de uma cultura, fatores como disponibilidade hídrica, tipo de solo ou incidência de pragas podem levar a resultados divergentes em parcelas específicas.

19.1 Variável Resposta e Variável Explicativa

No delineamento de estudos e na análise de dados, distinguimos:

Uma variável resposta (ou dependente) que mensura o resultado de um estudo ou o fenômeno de interesse.
Uma variável explicativa (ou independente) que visa elucidar ou influenciar as variações observadas na variável resposta.

Exemplos:

Produtividade Agrícola e Adubação: Um agrônomo conduz um experimento aplicando diferentes doses de um novo fertilizante fosfatado (variável explicativa) em parcelas de soja e mede a produtividade final de grãos (variável resposta) em cada parcela.
Qualidade da Água e Uso do Solo: Um ecólogo monitora a concentração de nitrato (variável resposta) em diversos riachos de uma bacia hidrográfica e coleta dados sobre a porcentagem de área agrícola (variável explicativa) no entorno de cada ponto de coleta.
Diversidade de Espécies e Fragmentação Florestal: Em um estudo sobre biodiversidade, pesquisadores medem o número de espécies de aves (variável resposta) em fragmentos florestais de diferentes tamanhos (variável explicativa).

Nem sempre o objetivo é estabelecer uma relação causal direta, podendo o estudo ser descritivo. Por exemplo, um levantamento florístico que cataloga as espécies presentes e suas abundâncias em diferentes fitofisionomias pode não definir a priori variáveis explicativas e respostas, mas sim buscar padrões de associação. A clareza na definição dessas variáveis depende intrinsecamente dos objetivos do estudo e do desenho experimental ou observacional adotado.

19.2 Diagrama de Dispersão

A visualização da relação entre duas variáveis quantitativas é eficazmente realizada por meio de um diagrama de dispersão. Este gráfico exibe a relação entre duas variáveis quantitativas mensuradas nos mesmos indivíduos ou unidades amostrais.

Os valores da variável explicativa são usualmente plotados no eixo horizontal (eixo x).
Os valores da variável resposta são plotados no eixo vertical (eixo y).
Cada unidade amostral (e.g., parcela experimental, ponto de coleta, fragmento florestal) é representada por um ponto no gráfico.

Exemplo 19.1 (Diagrama de Dispersão) Consideremos um estudo que investiga a relação entre a lâmina de irrigação (%) aplicada em uma cultura de aveia e a produção (em g/parcela). Os dados foram coletados de diferentes talhões de uma fazenda experimental. Os dados estão disponíveis em aveia.csv.

ggplot(aveia, aes(x = lamina, y = prod)) +
  geom_point() +
  labs(
    title = "Diagrama de Dispersão: Lâmina de irrigação vs. Produtividade de aveia",
    x = "Lâmina de irrigação (%)",
    y = "Produção de aveia (g)"
  ) +
  theme_classic()

Neste caso:

A “lâmina de irrigação” é a variável explicativa.
A “produção de aveia” é a variável resposta.

O diagrama mostra uma direção nítida: um aumento na produção à medida que a lâmina de irrigação aumenta, caracterizando uma associação positiva. A forma da relação é aproximadamente linear em uma determinada faixa de lâminas. A intensidade da relação é determinada pela proximidade com que os pontos seguem essa forma linear. Se os pontos estiverem bem agrupados ao longo de uma linha imaginária, a relação é forte.

Conclusões preliminares sugerem que maiores lâminas de irrigação tendem a resultar em maior produção, dentro da faixa estudada. Contudo, é importante lembrar que outros fatores não controlados (e.g., variabilidade do solo, microclima) podem influenciar a produção e que a relação pode não ser linear indefinidamente.

19.3 Correlação

A correlação (r), frequentemente chamada de coeficiente de correlação de Pearson (ou r de Pearson), é uma medida quantitativa da direção e intensidade da associação linear entre duas variáveis quantitativas, eliminando a subjetividade da interpretação puramente gráfica.

A percepção visual da intensidade de uma relação em um diagrama de dispersão pode ser influenciada pela escala dos eixos. Dois gráficos com os mesmos dados, mas escalas diferentes, podem transmitir impressões distintas da força da relação.

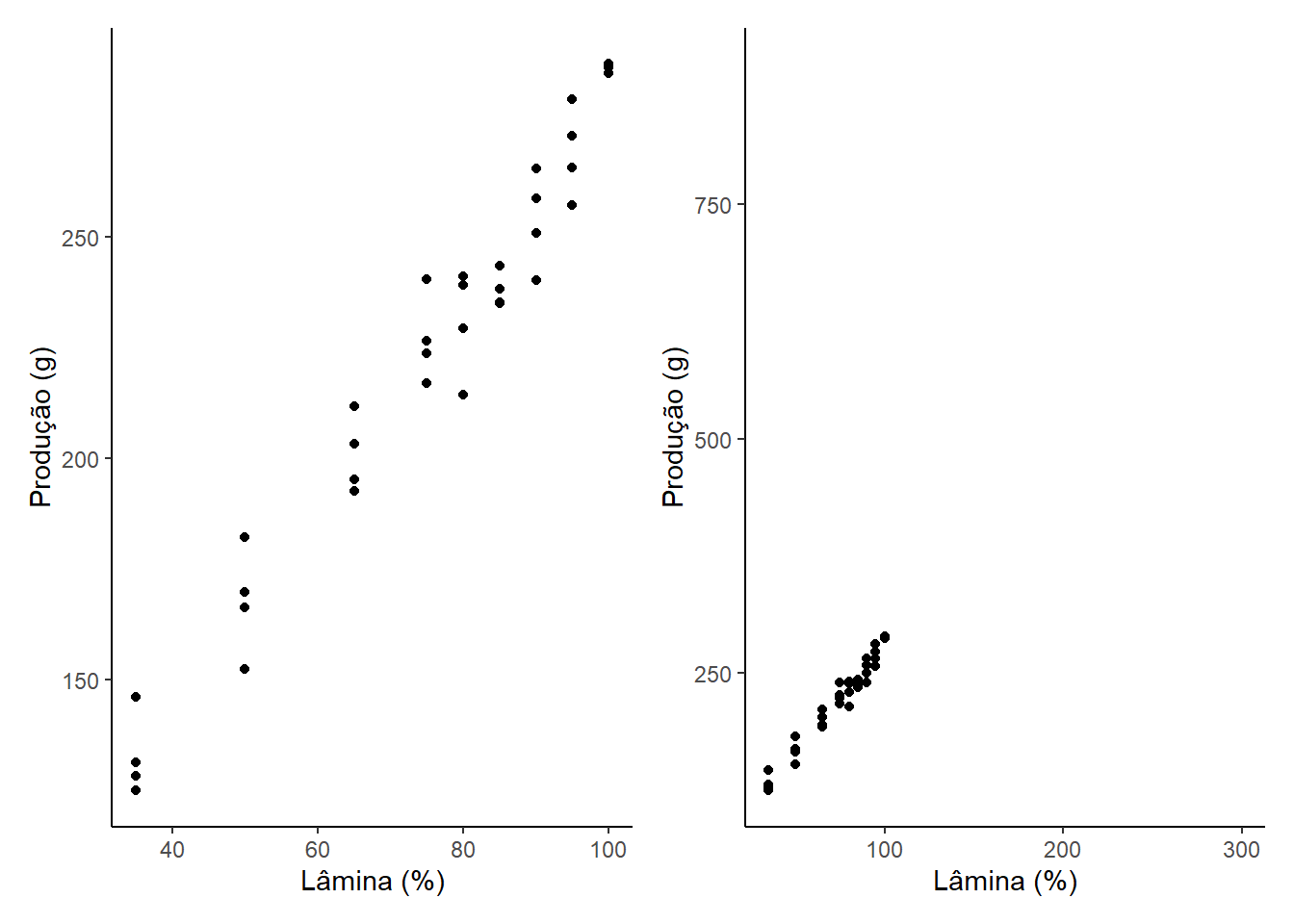
Os dois diagramas de dispersão representam exatamente os mesmos dados, porém o gráfico à direita foi desenhado em tamanho menor em um grande espaço. O gráfico à direita parece mostrar uma relação linear mais forte.

Exemplo 19.2 (Correlação) Para o estudo da relação entre lâmina de irrigação e produção de aveia, o cálculo do coeficiente de correlação de Pearson (r) resultou em 0,9805. Isso indica uma forte associação linear positiva.

cor(aveia)

          lamina      prod
lamina 1,0000000 0,9805307
prod   0,9805307 1,0000000

19.3.1 Propriedades da Correlação (r):

Não há distinção entre variável explicativa e resposta no cálculo de r. A correlação entre N e produtividade é a mesma que entre produtividade e N.
r não se altera com a mudança nas unidades de medida das variáveis x ou y. (e.g., produtividade em kg/ha ou t/ha).
r é sempre um número entre -1 e 1.
Valores positivos indicam associação positiva (ambas as variáveis tendem a aumentar ou diminuir juntas).
Valores negativos indicam associação negativa (quando uma variável aumenta, a outra tende a diminuir).
Valores próximos de 0 indicam uma relação linear muito fraca.
A intensidade da relação linear aumenta à medida que r se afasta de 0 em direção a -1 ou 1.

19.4 Regressão

Enquanto a correlação mede a força e a direção da associação linear, uma reta de regressão descreve essa relação, resumindo como a variável resposta (y) muda à medida que a variável explicativa (x) muda. Frequentemente, o objetivo é utilizar a reta de regressão para predizer o valor de y para um determinado valor de x.

A equação de uma regressão linear simples é: \[ y=a+b \cdot x \]

Em que:

‘b’ é a inclinação (ou coeficiente angular): a variação média em y quando x aumenta uma unidade.
‘a’ é o intercepto (ou coeficiente linear): o valor predito de y quando x=0. (A interpretação do intercepto requer cautela, especialmente se x=0 estiver fora da faixa observada dos dados – constituindo uma extrapolação).

Exemplo 19.3 (Regressão) Para os dados de lâmina de irrigação (x) e produção de aveia (y), ajustamos uma reta de regressão.

reg_aveia <- lm(prod ~ lamina, data = aveia)
coef(reg_aveia)

(Intercept)      lamina 
  52,253746    2,277365

\[ produtividade = 52,25 + 2,28\cdot x \]

Interpretação:

Intercepto (a = 52,25 g): A produção estimada de aveia seria de 52,25 g na ausência de aplicação de irrigação (se x=0 for um valor plausível e dentro ou próximo do intervalo de dados). Esse valor pode não ser realista, se a produção for impossível com uma lâmina zero de irrigação.
Inclinação (b = 2,28 g por % de lâmina): Para cada 1% de incremento na lâmina de irrigação, espera-se um aumento médio de 2,28 g na produção de aveia, dentro da faixa de doses estudada.

É comum apresentar a reta de regressão ajustada sobreposta ao diagrama de dispersão, frequentemente acompanhada da equação e do coeficiente de determinação (R² ou R²_ajustado), que indica a proporção da variância de y que é explicada pela variável x.

19.4.1 Inferência para Regressão

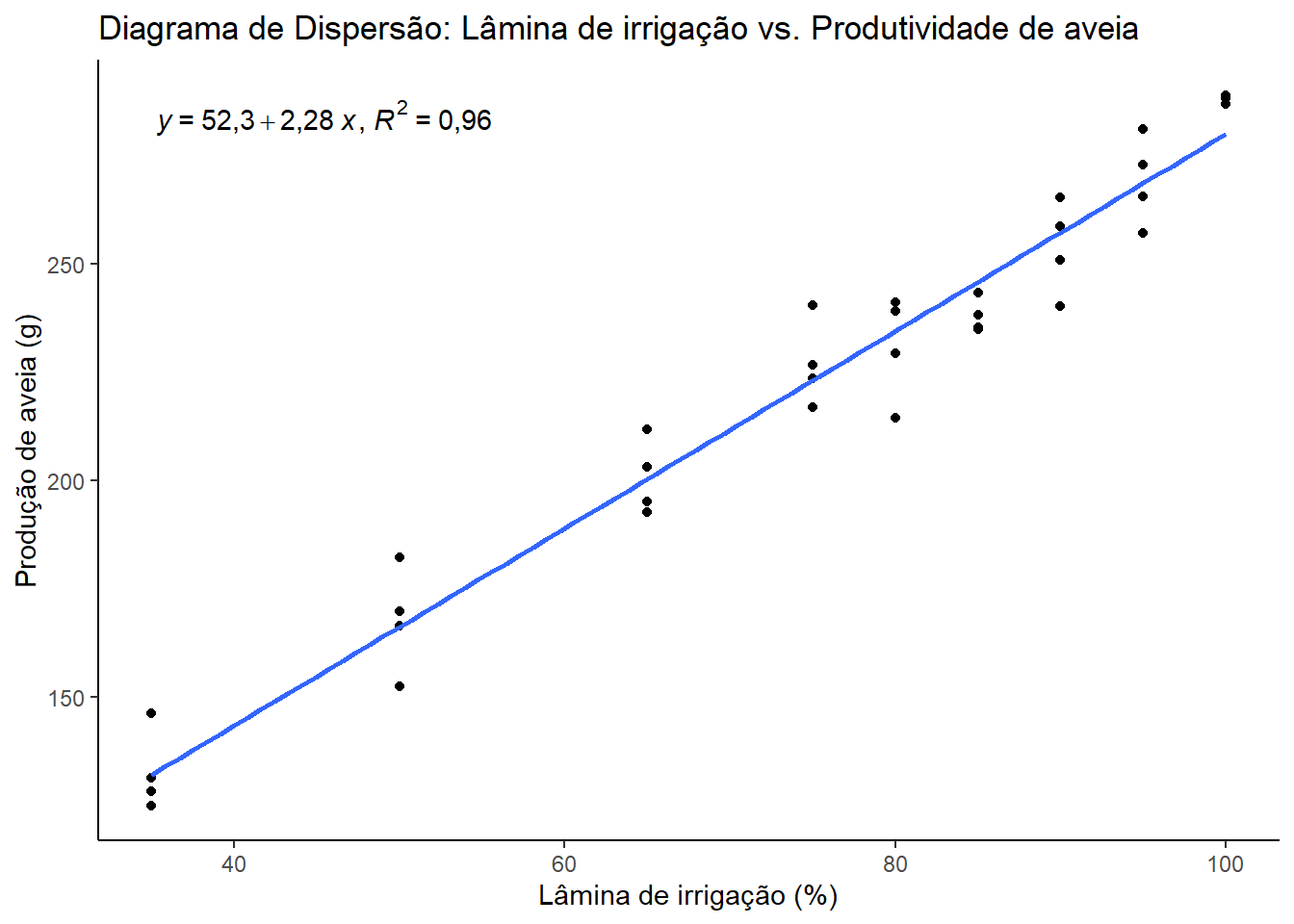
A análise de regressão vai além da simples descrição, permitindo a inferência estatística sobre a relação na população da qual a amostra foi extraída. Questões centrais incluem:

Existe uma relação linear estatisticamente significativa entre x e y na população, ou o padrão observado na amostra poderia ter surgido ao acaso?
Qual é a estimativa da inclinação (β) da reta de regressão populacional, incluindo uma margem de erro (intervalo de confiança) para essa estimativa?
Se usarmos a reta de regressão para predizer y para um dado valor de x, quão precisa é essa predição (incluindo uma margem de erro)?

A reta de regressão para a população é modelada como:

\[ y=\alpha + \beta \cdot x \]

A inferência frequentemente testa as seguintes hipóteses sobre a inclinação populacional (\(\beta\)):

H₀: \(\beta = 0\) (Não há relação linear entre x e y na população; a inclinação é zero, indicando uma reta horizontal ).

H₁: \(\beta \ne 0\) (Existe uma relação linear entre x e y na população).

Exemplo 19.4 (Inferência para Regressão) Continuando com o exemplo da lâmina de irrigação e produção de aveia, a análise de regressão nos fornece um p-valor para o coeficiente de inclinação:

summary(reg_aveia)


Call:
lm(formula = prod ~ lamina, data = aveia)

Residuals:
     Min       1Q   Median       3Q      Max 
-20,1129  -6,6153   0,3609   7,2157  17,3139 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 52,25375    6,07683   8,599  4,8e-10 ***
lamina       2,27736    0,07822  29,116  < 2e-16 ***
---
Signif. codes:  0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1

Residual standard error: 9,515 on 34 degrees of freedom
Multiple R-squared:  0,9614,    Adjusted R-squared:  0,9603 
F-statistic: 847,8 on 1 and 34 DF,  p-value: < 2,2e-16

Como o p-valor é menor que 0,05, rejeita-se H₀, concluindo que há evidência estatística de que a lâmina de irrigação influencia significativamente a produção de aveia.

Também é possível obter o intervalo de confiança para os parâmetros.

confint(reg_aveia)

               2,5 %   97,5 %
(Intercept) 39,90415 64,60335
lamina       2,11841  2,43632

19.4.2 Inferência sobre Predição

Além de inferir sobre os parâmetros do modelo, um uso importante da regressão é a predição de valores futuros ou não observados da variável resposta, acompanhada de uma medida de incerteza (intervalo de predição).

Exemplo 19.5 (Inferência sobre Predição) Um pesquisador estudou a relação entre a biomassa de serapilheira (folhas secas acumuladas, em g/m², variável explicativa) e a densidade de colêmbolos (um tipo de microartrópode do solo, em indivíduos/m², variável resposta) em diferentes pontos de uma floresta nativa. Os dados foram coletados (serrapilheira.csv) e um modelo de regressão linear foi ajustado.

O modelo ajustado para regressão linear é:

reg_serrapilheira <- lm(colembolo ~ biomassa, data = serrapilheira)
coef(reg_serrapilheira)

(Intercept)    biomassa 
 159,677780    2,320508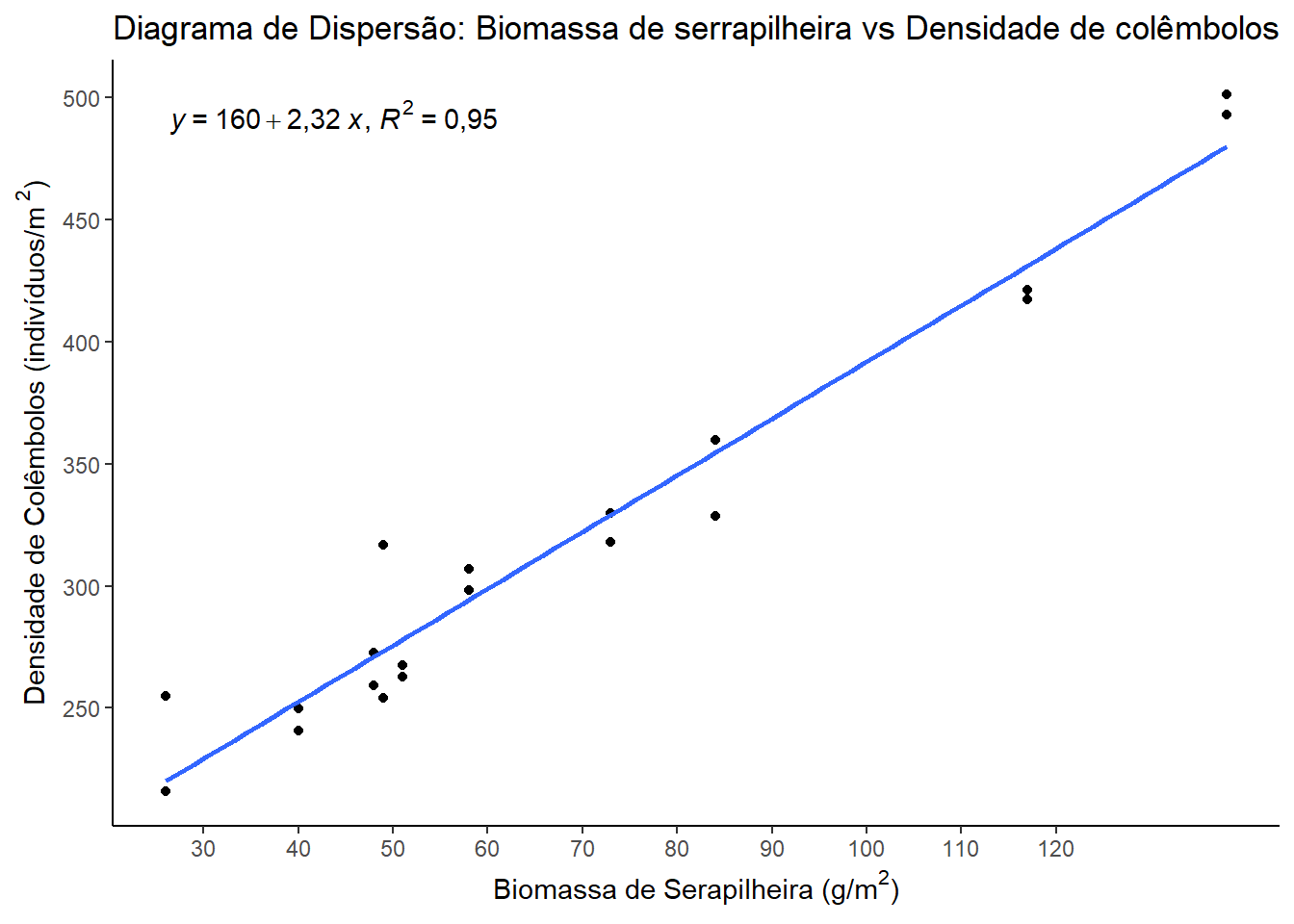

Deseja-se predizer a densidade de colêmbolos para um novo ponto na floresta onde a biomassa de serapilheira medida foi de 80 g/m², e também obter um intervalo de confiança de 95% para essa predição.

A predição pontual seria:

\(y = 159,68 + 2,32 \cdot 80 = 345,32\) indivíduos/m²

O intervalo de confiança pode ser calculado com a função predict:

predict(reg_serrapilheira, data.frame(biomassa = 80), interval = "predict")

       fit     lwr      upr
1 345,3184 305,768 384,8687

Conclusão: Com 95% de confiança, estima-se que a densidade de colêmbolos em um local com 80 g/m² de serapilheira esteja entre 305,77 e 384,87 indivíduos/m². Este intervalo é mais amplo que o intervalo de confiança para a média de y em um dado x, pois considera tanto a incerteza na estimativa da reta de regressão quanto a variabilidade individual dos dados em torno da reta.