7  Estatística Descritiva

7.1 Medidas de centro

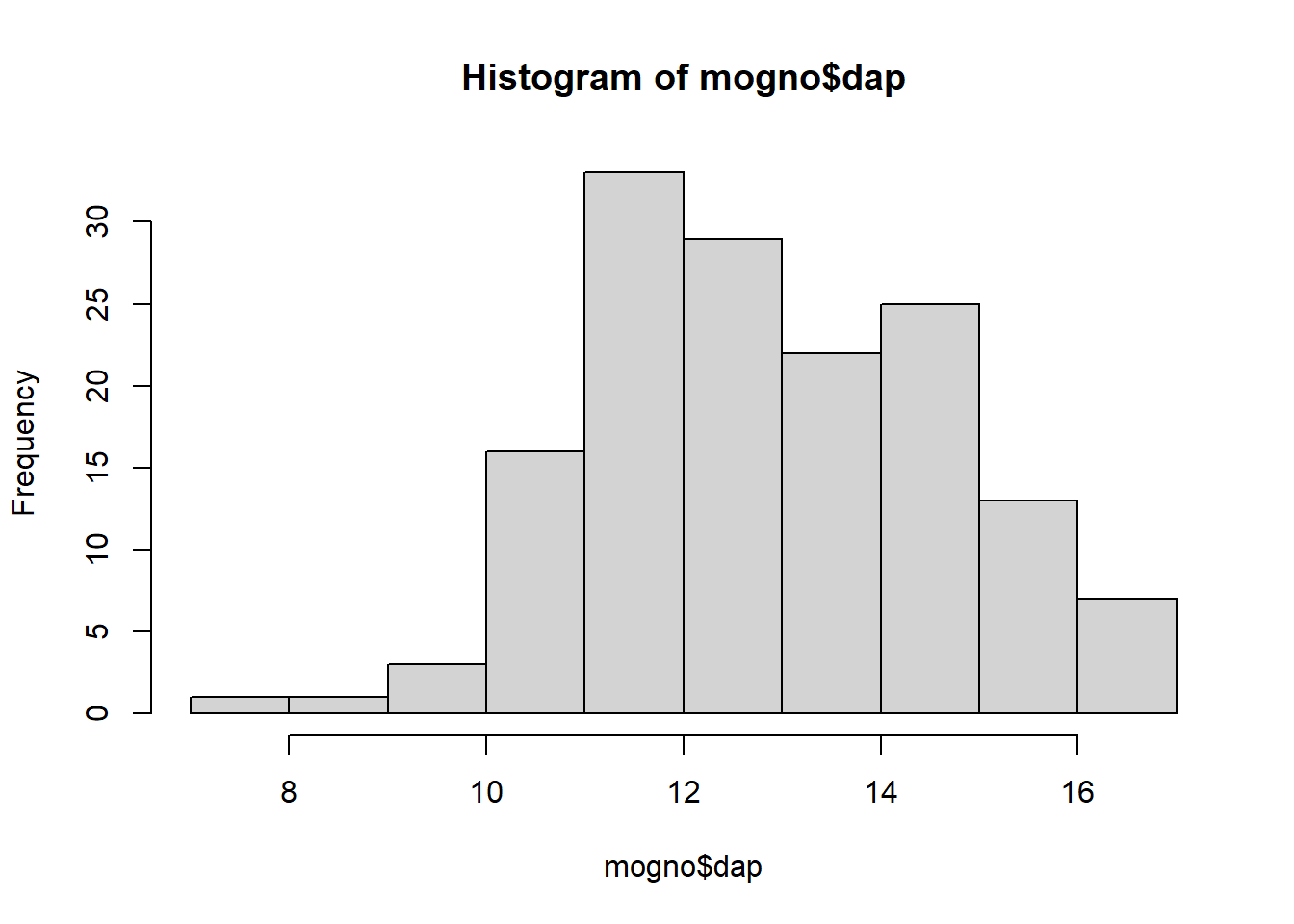
As medidas de centro, também conhecidas como medidas de tendência central, são ferramentas essenciais na estatística descritiva. Elas buscam resumir um conjunto de dados em um único valor que represente o “centro” ou a localização típica dos dados. As medidas de centro mais comuns são a média, a mediana e a moda.

Média

A média aritmética, frequentemente chamada apenas de “média”, é a soma de todos os valores em um conjunto de dados dividida pelo número de valores. É uma medida sensível a valores extremos (outliers), pois todos os valores contribuem igualmente para o cálculo da média.

Mediana

A mediana é o valor que divide um conjunto de dados ordenado em duas metades iguais. É uma medida robusta a outliers, pois não é afetada por valores extremos.

Exemplo 7.1 (Medidas de centro) Considere o conjunto de dados mogno.csv descrito na Seção A.1.

Qual a média e qual a mediana destes dados?

mogno <- read.csv("mogno.csv")  # Importando os dados

# média
mean(mogno$dap)

# mediana
median(mogno$dap)

O resultado nos mostra que a média dos dados é igual a 12,95 cm, e a mediana é igual a 12,82 cm.

7.2 Medidas de dispersão

As medidas de dispersão, também conhecidas como medidas de variabilidade, são ferramentas estatísticas que descrevem a variabilidade ou dispersão dos dados em torno de um ponto central, como a média ou a mediana. Elas fornecem informações importantes sobre a heterogeneidade dos dados e complementam as medidas de centro na descrição de uma distribuição.

7.2.1 Amplitude e Quartis

A amplitude é a medida de dispersão mais simples, calculada como a diferença entre o maior e o menor valor em um conjunto de dados. No entanto, a amplitude é sensível a valores extremos (outliers) e não considera a distribuição dos dados entre o mínimo e o máximo.

Os quartis são valores que dividem um conjunto de dados ordenado em quatro partes iguais.

  • O primeiro quartil (Q1) representa 25% (1/4) dos valores.
  • O segundo quartil (Q2) coincide com a mediana (50% ou 1/2 dos valores).
  • O terceiro quartil (Q3) representa 75% (3/4) dos valores.

A diferença entre o terceiro e o primeiro quartil é chamada de amplitude interquartil (AIQ), e representa a dispersão dos 50% centrais dos dados.

7.2.2 Resumo de cinco números:

O resumo de cinco números é uma forma concisa de descrever a distribuição de um conjunto de dados, incluindo as seguintes medidas:

  • Valor mínimo
  • Primeiro quartil (Q1)
  • Mediana (Q2)
  • Terceiro quartil (Q3)
  • Valor máximo

Exemplo 7.2 (Resumo dos cinco números) Considere o conjunto de dados mogno.csv descrito na Seção A.1.

Qual o resumo de cinco números e a amokitude interquartil para estes dados?

# resumo de cinco números
quantile(mogno$dap)

O resumo de cinco números fornece uma descrição concisa da distribuição do DAP, incluindo:

  • O menor valor de DAP observado no conjunto de dados foi 7,92 cm.
  • 25% das árvores têm DAP menor ou igual a 11,62 cm.
  • Metade das árvores (50%) têm DAP menor ou igual a 12,82 cm.
  • 75% das árvores têm DAP menor ou igual a 14,32 cm.
  • O maior valor de DAP observado no conjunto de dados foi 16,83
# Amplitude interquartil
IQR(mogno$dap)

A amplitude interquartil (AIQ), indica que os 50% centrais dos dados estão concentrados em um intervalo de 2,71 cm.

7.2.3 Variância, desvio-padrão e coeficiente de variação

A variância e o desvio padrão são medidas de dispersão que consideram a distância de cada valor em relação à média do conjunto de dados. A variância (s2) é a média dos quadrados das diferenças entre cada valor e a média. O desvio padrão (s) é a raiz quadrada da variância.

Quanto maior a variância, maior a dispersão dos dados em torno da média. O desvio padrão é expresso na mesma unidade dos dados originais, o que facilita a interpretação. Um desvio padrão maior indica maior variabilidade nos dados.

O coeficiente de variação é uma medida de dispersão relativa que representa o desvio padrão como uma porcentagem da média. Isso permite comparar a variabilidade de conjuntos de dados com unidades diferentes, já que a variabilidade é apresentada em termos percentuais em relação à média. Ele é calculado pela seguinte fórmula:

\[ CV = \frac{Desvio\ Padrão}{Média} * 100% \]

Exemplo 7.3 (Variância e desvio-padrão) Considere o conjunto de dados mogno.csv descrito na Seção A.1.

Qual a variância, o desvio-padrão 1 e o coeficiente de variação destes dados?

# Variância
var(mogno$dap)

# Desvio-padrão
sd(mogno$dap)

# Coeficiente de variação
sd(mogno$dap) / mean(mogno$dap) * 100

A variância é igual a 3,17.

O desvio-padrão é 1,78 cm. Indica que, em média, os valores de DAP se desviam 1,78 cm da média.

O CV do DAP das árvores de mogno é de 13,75 %. Isso significa que o desvio padrão representa 13,75 % da média.

7.3 Assimetria e Curtose

As medidas de assimetria e curtose fornecem informações adicionais sobre a forma da distribuição dos dados, complementando as medidas de centro e dispersão.

A assimetria é uma medida estatística que quantifica o grau de desvio da simetria em uma distribuição de dados. Em outras palavras, ela indica o quão “inclinada” a distribuição está para um lado ou para o outro. Uma distribuição perfeitamente simétrica tem assimetria igual a zero. Uma distribuição assimétrica à direita tem a cauda direita mais longa e assimetria positiva. Uma distribuição assimétrica à esquerda tem a cauda esquerda mais longa e assimetria negativa.

Na prática, valores muito altos (positivos ou negativos) indicam um forte desvio da simetria. Distribuições com assimetria entre -0.5 e +0.5 são geralmente consideradas aproximadamente simétricas. Valores entre -1 e -0.5 ou entre +0.5 e +1 sugerem uma assimetria moderada, enquanto valores menores que -1 ou maiores que +1 indicam uma assimetria mais pronunciada.

Já a curtose mede o grau de achatamento de uma distribuição em relação a uma distribuição normal. Para facilitar a interpretação, muitas vezes utilizamos o excesso de curtose, que é calculado subtraindo 3 do valor da curtose. Dessa forma, a distribuição normal, com curtose 3, terá excesso de curtose igual a zero. Com base no excesso de curtose, podemos classificar as distribuições em:

  • Leptocúrtica (excesso de curtose positivo): A distribuição é mais “pontuda” que a normal, com caudas mais pesadas, o que indica maior concentração de valores em torno da média e maior probabilidade de valores extremos (outliers).
  • Platicúrtica (excesso de curtose negativo): A distribuição é mais “achatada” que a normal, com caudas mais leves, o que indica menor concentração de valores em torno da média e menor probabilidade de valores extremos.
  • Mesocúrtica (excesso de curtose próximo de zero): A distribuição tem “achatamento” similar à normal.

Exemplo 7.4 (Assimetria e curtose) Considere o conjunto de dados mogno.csv descrito na Seção A.1.

Qual a assimetria e curtose desses dados?

Existem diferentes pacotes em R para calcular a assimetria e a curtose. Um pacote popular é o moments2:

pacman::p_load("moments") # instalar e/ou carregar o pacote moments

# Assimetria
skewness(mogno$dap)

# Curtose
kurtosis(mogno$dap)

A assimetria é igual a 0,052. Um valor próximo de zero indica que a distribuição do DAP é aproximadamente simétrica.

A curtose é igual a 2,48. Indica que a distribuição é platicúrtica, ou seja, mais “achatada” que a distribuição normal. Isso significa que os dados estão mais dispersos em torno da média, com caudas mais leves e menor concentração de valores no centro da distribuição.

7.4 Descrição de uma distribuição

A descrição completa de uma distribuição de dados vai além da simples apresentação de tabelas e números. Ela envolve a combinação de medidas numéricas e representações gráficas para revelar a forma, o centro, a dispersão e a presença de valores atípicos nos dados. Essa análise exploratória é crucial para a compreensão dos padrões e das características dos dados, orientando a escolha de métodos estatísticos mais avançados e a interpretação dos resultados.

Utilize as medidas numéricas, apresentadas nas seções anteriores juntamente com representações gráficas, como histogramas, boxplots e diagramas de ramo e folhas, que permitem visualizar a forma da distribuição, identificar a presença de assimetria e outliers, e obter uma compreensão mais intuitiva dos dados.

Ao descrever uma distribuição, considere os seguintes aspectos:

  • Forma: A distribuição é simétrica, assimétrica à direita ou assimétrica à esquerda?
  • Centro: Qual é a medida de centro mais representativa (média, mediana)?
  • Dispersão: Qual a variabilidade dos dados? Os dados estão concentrados ou dispersos?
  • Outliers: Existem valores atípicos? Se sim, como eles afetam a análise?

Exemplo 7.5 (Descrição de uma distribuição simétrica) Considere o conjunto de dados mogno.csv descrito na Seção A.1, que contém o diâmetro à altura do peito (DAP), em centímetros, de árvores de mogno.

Descrever a distribuição do DAP utilizando medidas numéricas e representações gráficas.

mogno <- read.csv("mogno.csv")  # Importando os dados

Medidas numéricas

Já foram apresentadas nos exemplos anteriores:

# média
mean(mogno$dap)

# mediana
median(mogno$dap)

# resumo de cinco números
quantile(mogno$dap)

# Variância
var(mogno$dap)

# Desvio-padrão
sd(mogno$dap)

# Coeficiente de variação
sd(mogno$dap) / mean(mogno$dap) * 100

pacman::p_load("moments") # instalar e/ou carregar o pacote moments

# Assimetria
skewness(mogno$dap)

# Curtose
kurtosis(mogno$dap)

Representações gráficas

A análise combinada de histograma, boxplot e diagrama de ramo-e-folhas oferece uma compreensão abrangente da distribuição dos dados.

# Histograma
hist(mogno$dap)

stem(mogno$dap)

  The decimal point is at the |

   7 | 9
   8 | 
   8 | 8
   9 | 
   9 | 89
  10 | 002344
  10 | 667889999
  11 | 0001111223444
  11 | 5556667777888889
  12 | 000000111122334
  12 | 5555666688888999999
  13 | 0133
  13 | 5555556678888888999
  14 | 11122233444
  14 | 55666788899
  15 | 000012234
  15 | 5666668
  16 | 02
  16 | 55778
# Box-plot
boxplot(mogno$dap)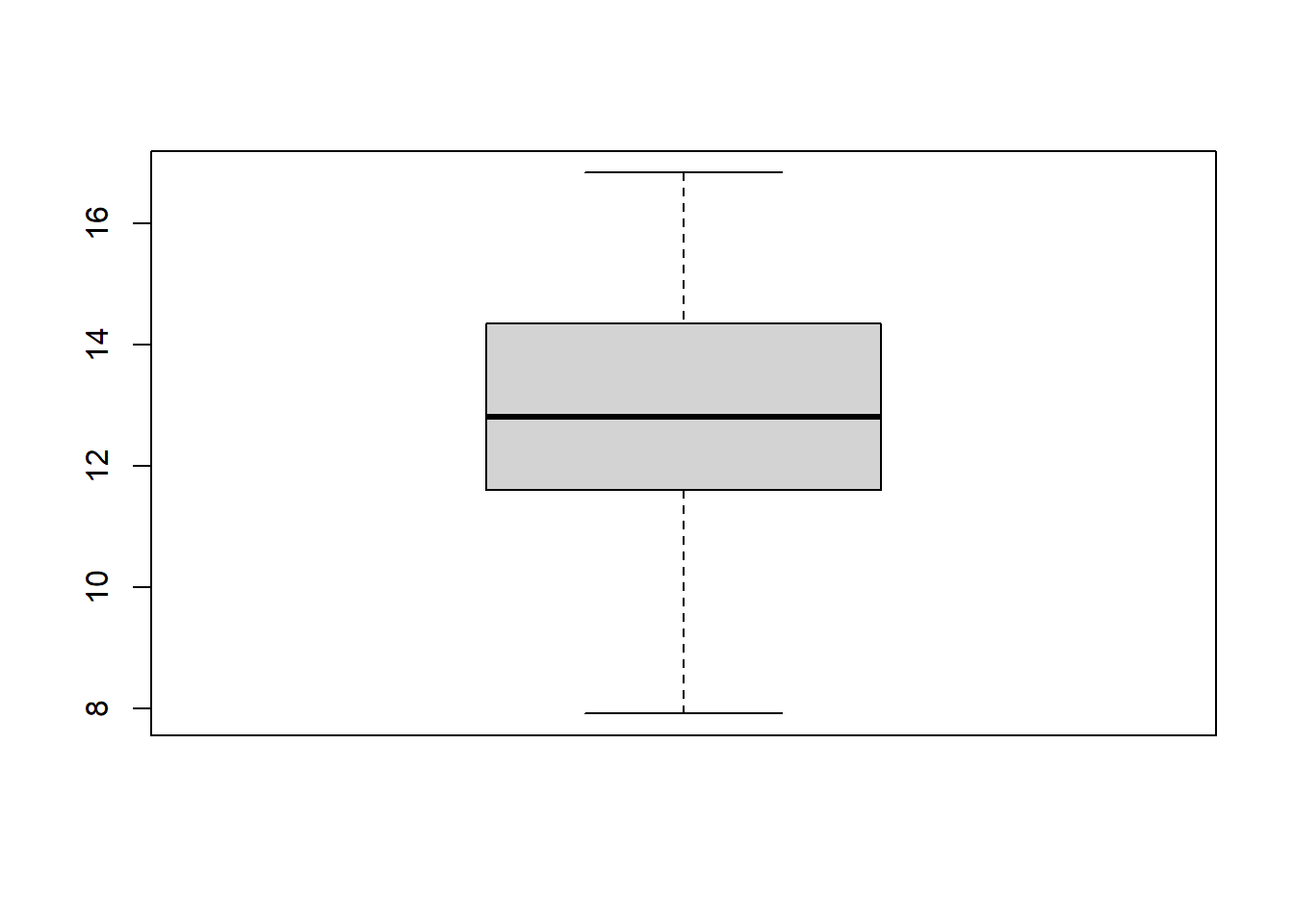

Análise da Distribuição:

  • Forma: Os gráficos indicam que a distribuição do DAP é aproximadamente simétrica, com a maioria dos valores concentrados em torno da média.
  • Centro: A média (12,95 cm) e a mediana (12,82 cm) são muito próximas, o que corrobora a simetria da distribuição.
  • Dispersão: O desvio padrão (1,78 cm) indica uma variabilidade moderada nos dados. A amplitude interquartil, observada no boxplot, reforça essa observação.
  • Outliers: O boxplot não indica a presença de outliers.

Conclusão:

A distribuição do DAP das árvores de mogno é aproximadamente simétrica, com valores concentrados em torno da média e sem a presença de outliers. A variabilidade dos dados é moderada, indicando que a maioria das árvores possui DAP similar.

O DAP média da população é de 12,95 cm com desvio-padrão de 1,78 cm.

7.4.1 Descrevendo outras distribuições

Vejamos outros exemplos com distribuições bastante diferentes da primeira.

Exemplo 7.6 (Descrição de uma distribuição assimétrica) Considere os dados do tempo de sobrevivência de insetos descritos na Seção A.3) (download do arquivo: inseto.csv).

inseto <- readr::read_csv("inseto.csv") # importando o arquivo

Medidas numéricas

# média
mean(inseto$sobrev)
[1] 113.19
# mediana
median(inseto$sobrev)
[1] 61
# resumo de cinco números
quantile(inseto$sobrev)
    0%    25%    50%    75%   100% 
  4.00  33.25  61.00 129.25 849.00 
# Variância
var(inseto$sobrev)
[1] 22594.6
# Desvio-padrão
sd(inseto$sobrev)
[1] 150.315
# Coeficiente de variação
sd(inseto$sobrev) / mean(inseto$sobrev) * 100
[1] 132.7988
pacman::p_load("moments") # instalar e/ou carregar o pacote moments
# Assimetria
skewness(inseto$sobrev)
[1] 2.897902
# Curtose
kurtosis(inseto$sobrev)
[1] 11.80371

Representações gráficas

# Histograma
hist(inseto$sobrev)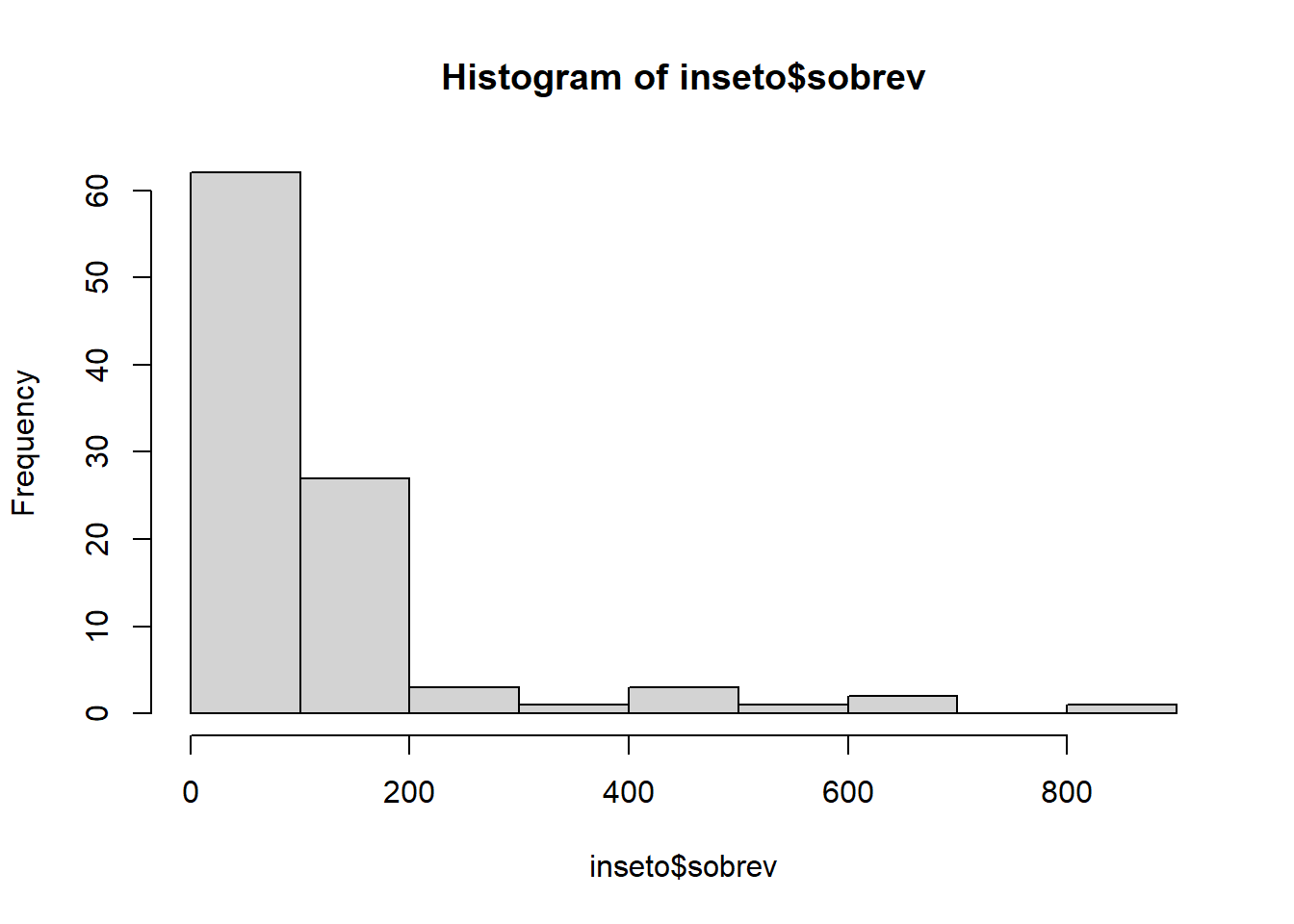

# Diagrama de ramo e folhas
stem(inseto$sobrev)

  The decimal point is 2 digit(s) to the right of the |

  0 | 01111111222222222233333333444444444455555555555666667777777889
  1 | 001122222223333344455567889
  2 | 445
  3 | 1
  4 | 29
  5 | 07
  6 | 78
  7 | 
  8 | 5
# Box-plot
boxplot(inseto$sobrev)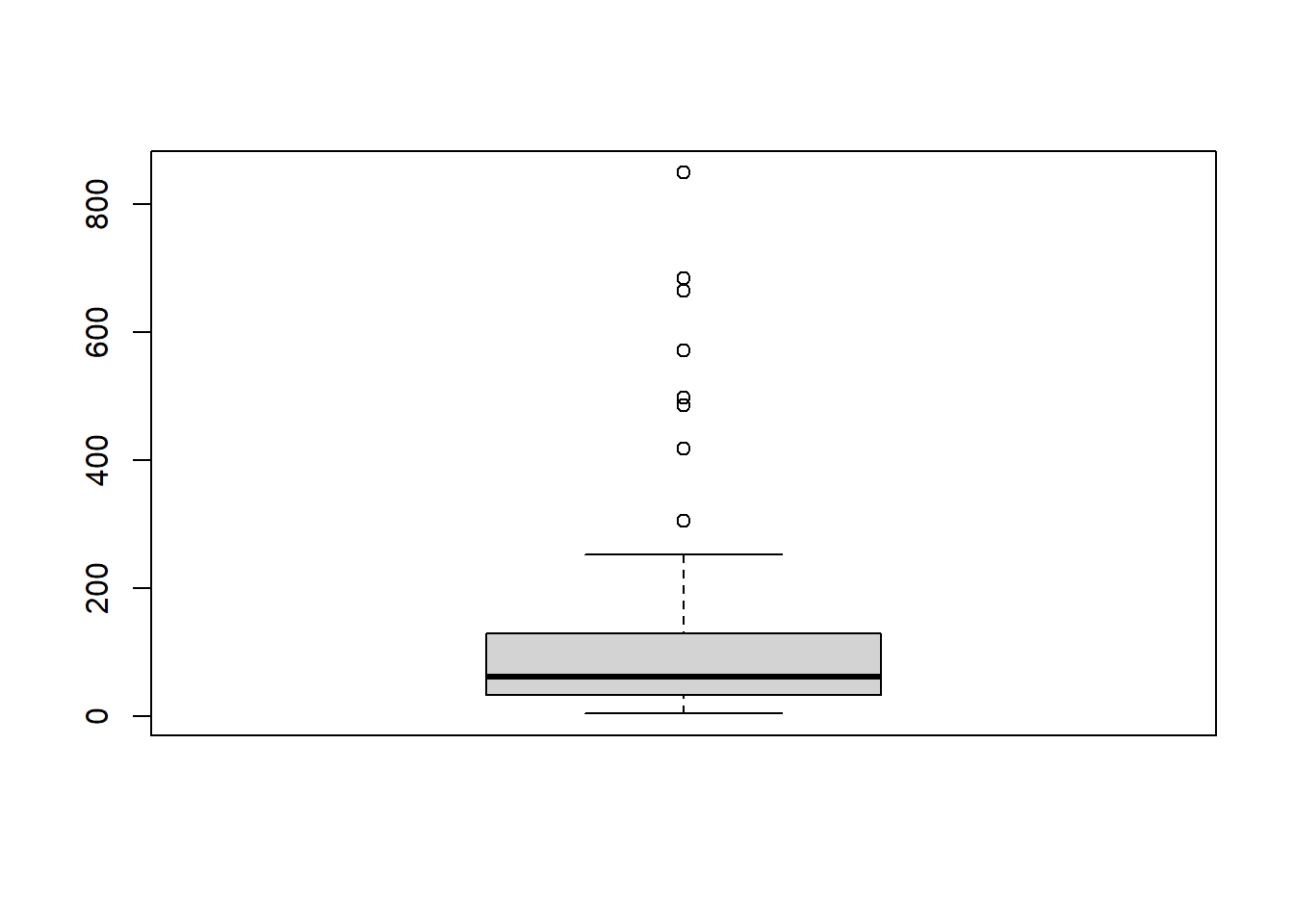

Análise da Distribuição:

  • Forma: O histograma e o boxplot indicam que a distribuição do tempo de sobrevivência é assimétrica à direita, com uma cauda longa se estendendo para valores mais altos.
  • Centro: A média (113,2 minutos) é maior que a mediana (61,00 minutos), o que é típico de distribuições assimétricas à direita.
  • Dispersão: O desvio padrão (150,3 minutos) e o coeficiente de variação (132,8%) indicam uma variabilidade considerável nos dados.
  • Outliers: O boxplot mostra a presença de alguns outliers, que representam insetos com tempo de sobrevivência muito maior que a maioria.

Conclusão:

A distribuição do tempo de sobrevivência dos insetos expostos ao inseticida é assimétrica à direita, com a maioria dos insetos sobrevivendo por um período relativamente curto e apenas alguns sobrevivendo por um período muito mais longo. A presença de outliers indica que alguns fatores podem estar influenciando a sobrevivência de alguns insetos de forma diferente dos demais, possivelmente devido a variações na resistência individual ou a diferenças na exposição ao inseticida.

O resumo de cinco números ( 4,0, 33,2, 61,0, 129,2, 849,0) mostra que metade dos insetos morrem dentro dos primeiros 61,0 minutos e quase nenhum sobrevive até 129,2 minutos. No entanto, alguns poucos insetos sobrevivem mais, de modo que o gráfico se estende mais para a direita do pico, até o valor mais alto de 849 minutos.

A assimetria à direita é um padrão comum em dados de tempo de sobrevivência, especialmente quando há alta mortalidade inicial e alguns indivíduos com alta resistência ou menor exposição ao fator de risco. A presença de outliers pode distorcer a média, tornando a mediana uma medida mais robusta para descrever o centro da distribuição.

Muitas vezes, uma distribuição pode apresentar dois (ou mais) picos. A existência de mais de um pico sugere que indívíduos de vários tipos estão misturados no conjunto de dados.

Exemplo 7.7 (Descrição de uma distribuição bimodal) Considere o conjunto de dados peixe.csv, decrito na Seção A.4, que contém o comprimento (em cm) de vários peixes apanhados em um rio.

Medidas numéricas

# média
mean(peixe$comp)
[1] 30.0745
# mediana
median(peixe$comp)
[1] 28.6
# resumo de cinco números
quantile(peixe$comp)
    0%    25%    50%    75%   100% 
 8.700 20.200 28.600 40.375 53.400 
# Variância
var(peixe$comp)
[1] 125.0334
# Desvio-padrão
sd(peixe$comp)
[1] 11.18183
# Coeficiente de variação
sd(peixe$comp) / mean(peixe$comp) * 100
[1] 37.18044
pacman::p_load("moments") # instalar e/ou carregar o pacote moments
# Assimetria
skewness(peixe$comp)
[1] 0.1376825
# Curtose
kurtosis(peixe$comp)
[1] 1.74875

Representações gráficas

# Histograma
hist(peixe$comp)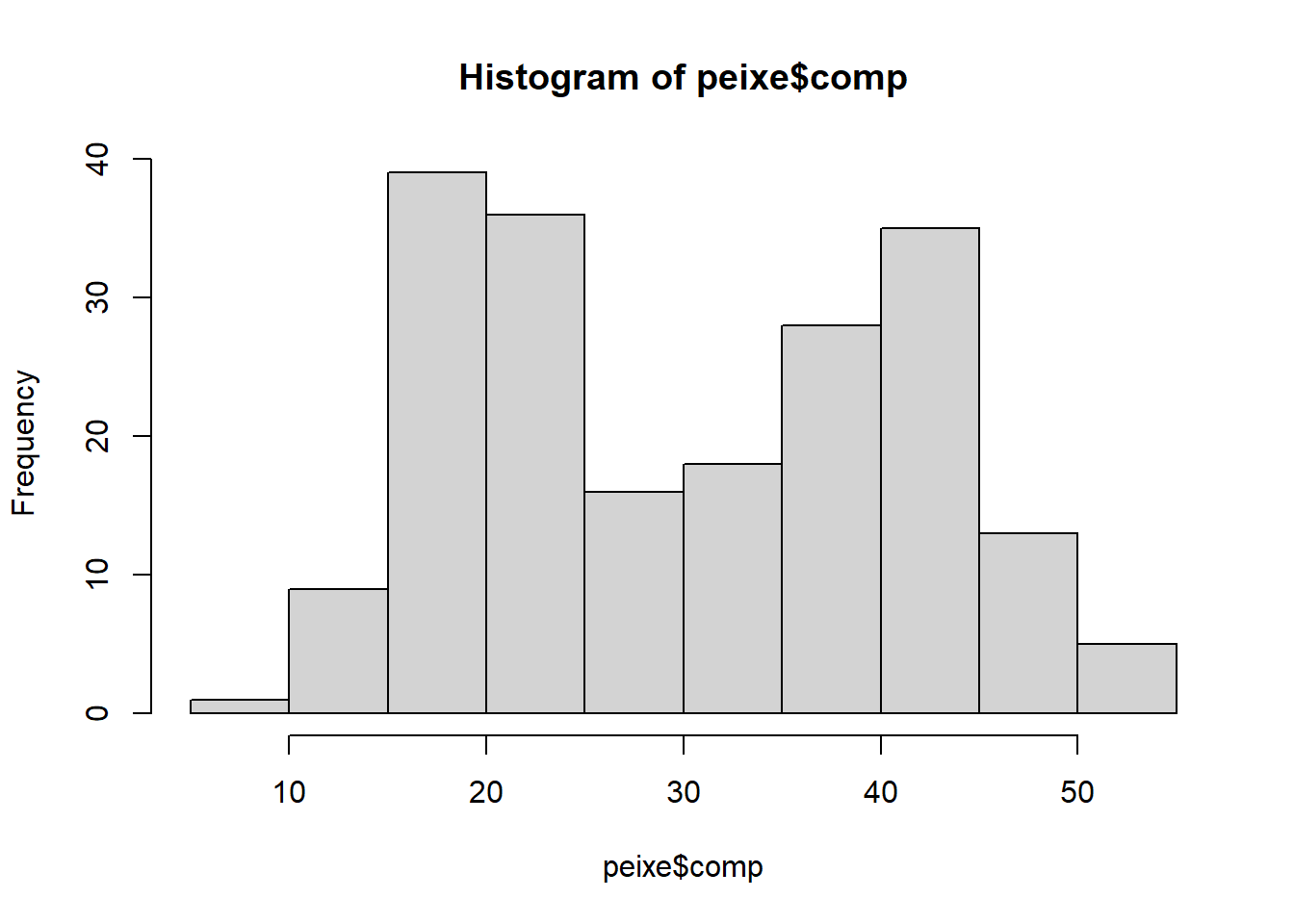

# Diagrama de ramo e folhas
stem(peixe$comp)

  The decimal point is at the |

   8 | 7
  10 | 37
  12 | 969
  14 | 23381112235667
  16 | 001334781667779
  18 | 0224550022668
  20 | 022489001233333789
  22 | 23794566779
  24 | 003566781136789
  26 | 111358
  28 | 057
  30 | 15458
  32 | 0512445578
  34 | 24811666
  36 | 246677782356778999
  38 | 06027
  40 | 133679011222689
  42 | 0014460012344559
  44 | 366813488
  46 | 1125
  48 | 0127
  50 | 88
  52 | 324
# Box-plot
boxplot(peixe$comp)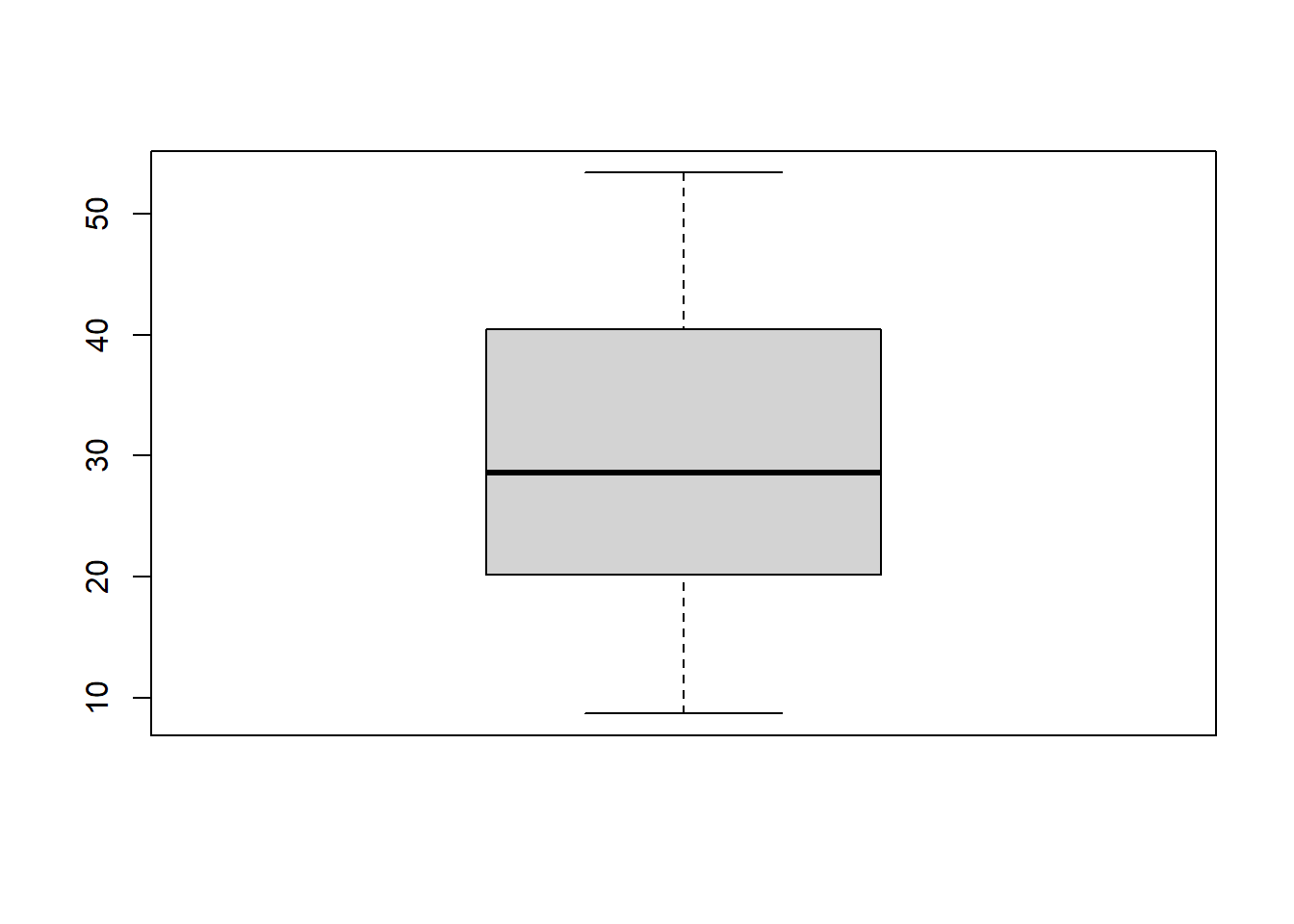

Análise da Distribuição:

  • Forma: O histograma indica que a distribuição do comprimento dos peixes é bimodal, com dois picos distintos em torno de 20 cm e 40 cm. Isso sugere a presença de dois grupos distintos de peixes, possivelmente machos e fêmeas, ou duas espécies diferentes.
  • Centro: A média (30,07 cm) e a mediana (28,6 cm) estão localizadas entre os dois picos, o que é típico de distribuições bimodais. Nesse caso, a média e a mediana não representam bem o centro da distribuição, pois a maioria dos valores se concentra nos dois picos.
  • Dispersão: O desvio padrão (11,18 cm) e o coeficiente de variação (37,18%) indicam uma variabilidade moderada nos dados, considerando a presença de dois grupos distintos.
  • Outliers: O boxplot não mostra a presença de outliers.

Conclusão:

A distribuição do comprimento dos peixes é bimodal, sugerindo a presença de dois grupos distintos na população. Essa bimodalidade pode ser explicada por diversos fatores, como dimorfismo sexual (machos e fêmeas com tamanhos diferentes), presença de duas espécies com comprimentos médios distintos ou variação no tamanho dos peixes em diferentes idades ou estágios de desenvolvimento.

A descrição da distribuição separada por sexo dos peixes pode ser bem mais útil.

# Histograma para peixes machos
peixe %>%
  filter(sexo == "m") %>%
  pull(comp) %>%
  hist()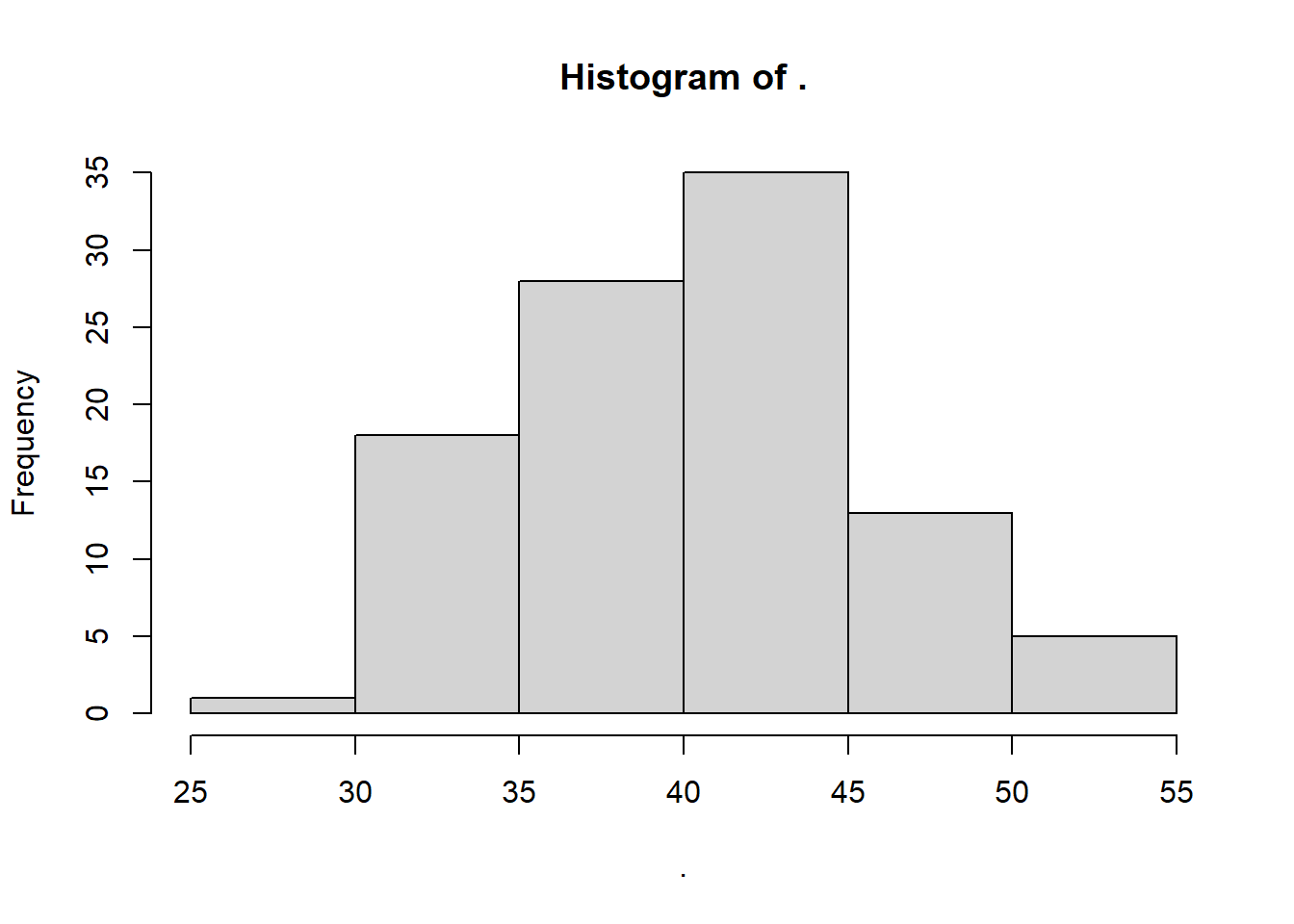

# Histograma para peixes fêmeas
peixe %>%
  filter(sexo == "f") %>%
  pull(comp) %>%
  hist()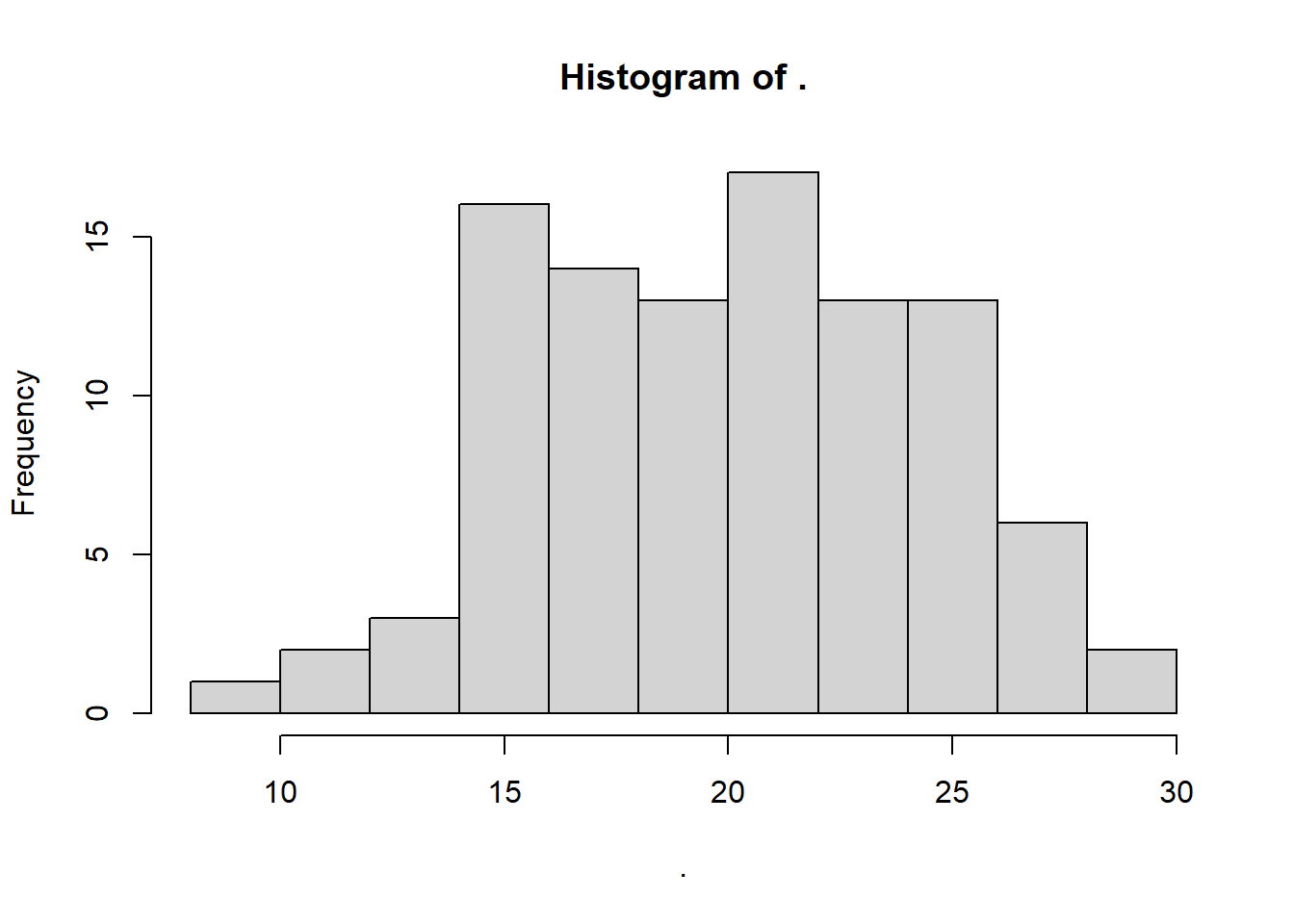

Por fim, pode haver nas distribuições um ou alguns poucos valores discrepantes, ou seja, valores que diferem consideravelmente dos demais. Muito frequentemente, também são chamados de outliers.

Exemplo 7.8 (Descrição de uma distribuição com valores discrepantes) Considere os dados de produção de morango (em g/planta) contidos no arquivo morango.csv.

Medidas numéricas

# média
mean(morango$prod)
[1] 883.7812
# mediana
median(morango$prod)
[1] 670
# resumo de cinco números
quantile(morango$prod)
     0%     25%     50%     75%    100% 
 568.00  628.25  670.00  772.25 6870.00 
# Variância
var(morango$prod)
[1] 1199974
# Desvio-padrão
sd(morango$prod)
[1] 1095.433
# Coeficiente de variação
sd(morango$prod) / mean(morango$prod) * 100
[1] 123.9485
pacman::p_load("moments") # instalar e/ou carregar o pacote moments
# Assimetria
skewness(morango$prod)
[1] 5.34003
# Curtose
kurtosis(morango$prod)
[1] 29.69773

Representações gráficas

# Histograma
hist(morango$prod)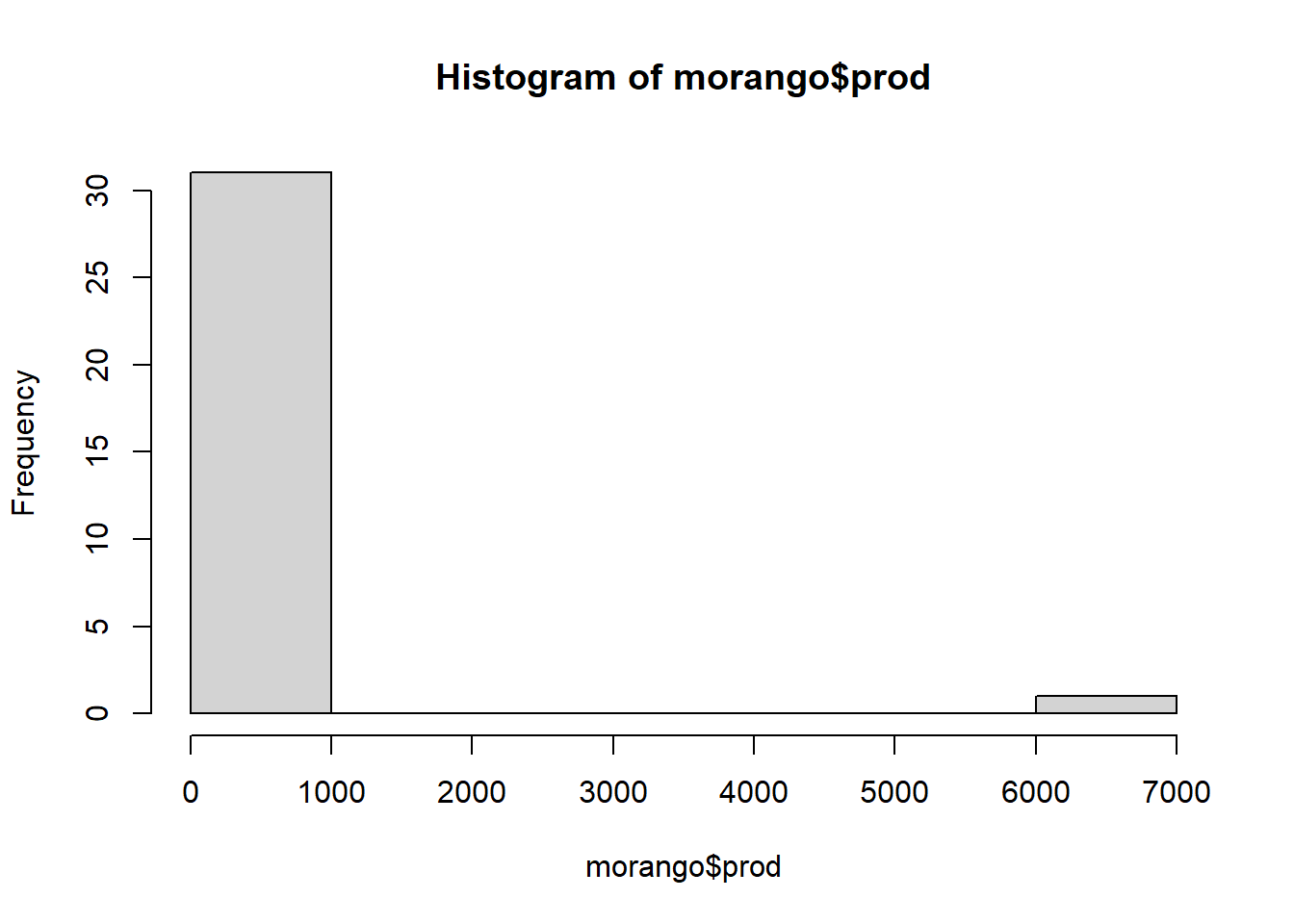

# Diagrama de ramo e folhas
stem(morango$prod)

  The decimal point is 3 digit(s) to the right of the |

  0 | 6666666666666777777778888888888
  1 | 
  2 | 
  3 | 
  4 | 
  5 | 
  6 | 9
# Box-plot
boxplot(morango$prod)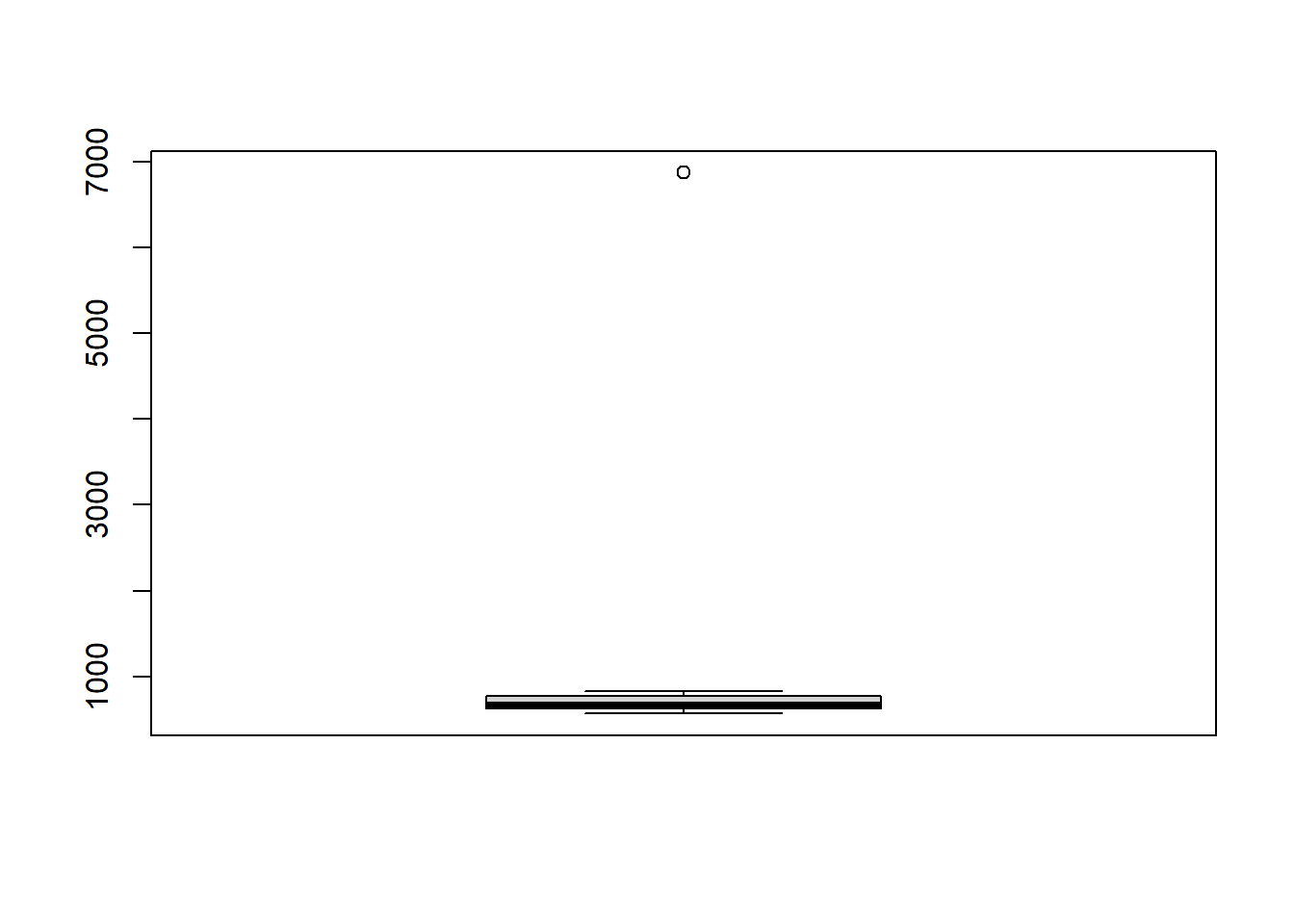

Análise da Distribuição:

  • Forma: O histograma e o boxplot indicam que a distribuição da produção de morangos é assimétrica à direita, com uma cauda longa se estendendo para valores mais altos.
  • Centro: A média (1503.78 kg/ha) é maior que a mediana (733 kg/ha), o que é típico de distribuições assimétricas à direita.
  • Dispersão: O desvio padrão (1865.87 kg/ha) e o coeficiente de variação (124.06%) indicam uma alta variabilidade nos dados.
  • Outliers: O boxplot mostra a presença de um outlier extremo, que representa uma planta com produção muito acima da média.

Conclusão:

Esta distribuição apresenta claramente um valor discrepante: 6870 g na posição 10 do conjunto de dados.

Ao se excluir este valor discrepante (outlier), veja como a distribuição se torna simétrica.

morango %>%
  filter(prod != max(prod)) %>%
  pull(prod) %>%
  hist()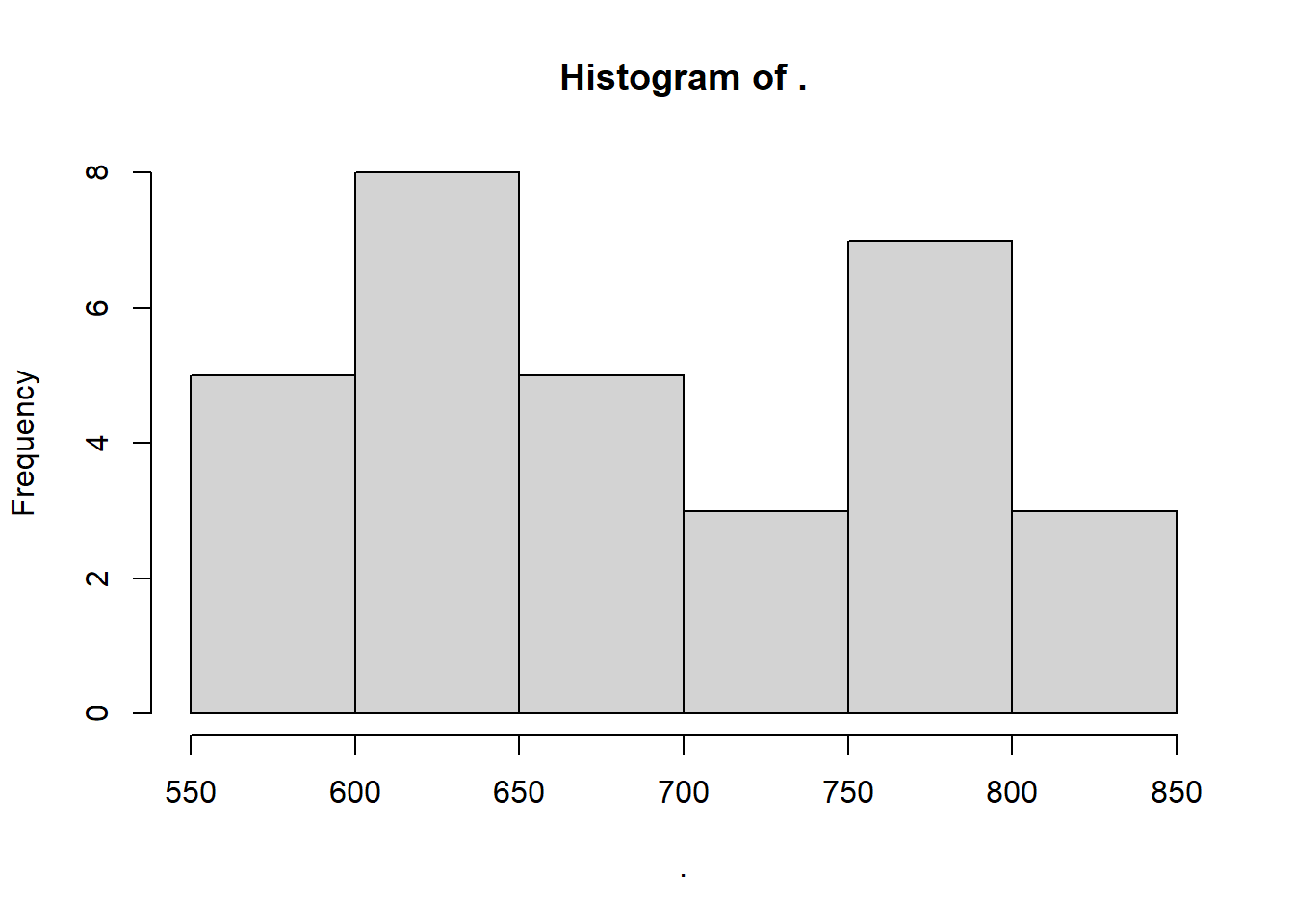

7.5 Relação entre medidas numéricas e representações gráficas:

As medidas numéricas e as representações gráficas são ferramentas complementares na análise descritiva de dados. As medidas numéricas fornecem informações quantitativas sobre a distribuição, enquanto as representações gráficas permitem visualizar a forma da distribuição e identificar padrões e características que podem não ser evidentes nos números.

  • Simetria: Uma distribuição simétrica terá média e mediana próximas, e o histograma apresentará uma forma semelhante em ambos os lados do centro.

  • Assimetria à direita: Uma distribuição assimétrica à direita (com cauda longa à direita) terá média maior que a mediana, e o histograma terá uma cauda mais longa à direita.

  • Assimetria à esquerda: Uma distribuição assimétrica à esquerda (com cauda longa à esquerda) terá média menor que a mediana, e o histograma terá uma cauda mais longa à esquerda.

  • Outliers: Outliers são pontos que se distanciam significativamente dos demais dados e podem ser identificados em boxplots como pontos isolados além dos “bigodes”.

  1. As funções var e sd utilizam o denominador n-1 no cálculo, que não é adequado para o cálculo da variância e desvio-padrão de uma população. No entanto, para uma população de tamanho grande, as diferenças são desprezíveis.↩︎

  2. veja a Seção 2.1 como instalar esse ou outros pacotes.↩︎