9  Inferência Estatística

A inferência estatística é um ramo fundamental da estatística que nos permite extrair conclusões sobre uma população a partir de uma amostra de dados. Ela é essencial para a pesquisa científica, pois permite que os pesquisadores generalizem as conclusões obtidas a partir de uma amostra para a população de interesse. Isso é fundamental para a tomada de decisão em diversas áreas, como saúde, agricultura, meio ambiente e políticas públicas.

A inferência estatística lida com a incerteza inerente ao processo de amostragem. Como a amostra é apenas uma parte da população, sempre há uma chance de que as conclusões obtidas não reflitam perfeitamente a realidade da população. A inferência estatística utiliza a teoria da probabilidade para quantificar essa incerteza e fornecer medidas de confiança nas conclusões.

As duas principais ferramentas da inferência estatística são:

Para garantir a validade das inferências realizadas com o teste t, é essencial que certas premissas sejam satisfeitas. Essas premissas são condições que, quando violadas, podem comprometer a confiabilidade dos resultados do teste. As principais premissas do teste t são:

A violação dessas premissas pode levar a resultados imprecisos ou enganosos. Se as premissas não forem satisfeitas, pode ser necessário usar um teste não paramétrico, que não exige que os dados sigam uma distribuição normal ou tenham variâncias iguais.

9.1 Intervalo de Confiança para a média populacional

Um intervalo de confiança (IC) é uma estimativa de um intervalo que contém um parâmetro populacional com um certo nível de confiança. O nível de confiança indica a probabilidade de que o intervalo contenha o parâmetro populacional.

Os níveis de confiança mais comuns são 90%, 95% e 99%. A escolha do nível de confiança afeta a amplitude do intervalo: quanto maior o nível de confiança, mais amplo será o intervalo.

Utilizaremos a função t.test para calcular um Intervalo de Confiança para a média.

Exemplo 9.1 (Intervalo de Confiança para a média) Considere o conjunto de dados da Seção A.2 que pode ser encontrado no arquivo mogno_am.csv. Calcule o Intervalo de Confiança com 95% 1 de probabilidade (IC95%) para a média populacional dos valores de DAP.

mogno_am <- read.csv("mogno_am.csv")  # Importando os dados
# IC 95%
t.test(mogno_am$dap)

    One Sample t-test

data:  mogno_am$dap
t = 23.04, df = 9, p-value = 2.598e-09
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 12.01668 14.63332
sample estimates:
mean of x 
   13.325

O output da função t.test contém muitas informações, mas por hora, vamos nos focar apenas no intervalo de confiança, indicado pelo texto 95 percent confidence interval

O intervalo de confiança para a média populacional está entre 12,02 cm e 14,63 cm. Em outras palavras, estamos 95% confiantes que a média populacional do DAP de árvores de Mogno Africano está compreendidade entre 12,02 cm e 14,63 cm.

O valor da média amostral, 13,32 cm, é a estimativa central e pode ser entendida como uma estimativa não enviesada da média populacional.

A amostra deste exemplo vem de uma população conhecida, cuja média populacional é 12,95 cm. Vejam que a média amostral e a média populacional diferem entre si, mas o IC calculado contém a média populacional.

A interpretação que devemos fazer do IC de 95% é que 95 em cada 100 amostragens feitas na população irão conter a média populacional. Vejamos a explicação no exemplo abaixo com o uso de simulação.

Exemplo 9.2 (Intervalo de Confiança para a média - simulações) Considere o conjunto de dados da Seção A.1, disponível em mogno.csv.

Inicialmente, criamos uma função que faz uma amostragem de n elementos e retorna os valores, inferior e superior, do IC calculado.

## Função que amostra n elementos e retorna os valores inferior e superior do IC calculado
## data = conjunto de dados de onde será retirada a amostra
## n_sample = tamanho da amostra
ic_amostr <- function(data, n_sample, ...) {
  ic_sample <- sample(data, n_sample) |> t.test(...)
  return(ic_sample$conf.int)
}

Em seguida, com o uso da função replicate, realizamos 100 simulações deste processo2:

## 100 simulações com a função replicate
ic_simul <- replicate(100, ic_amostr(mogno$dap, 10))
## mostrar apenas os primeiros valores do resultado
ic_simul  |> 
  t()  |> 
  head()
         [,1]     [,2]
[1,] 12.32345 14.97855
[2,] 11.38402 13.53198
[3,] 12.02412 14.16588
[4,] 11.28135 13.59465
[5,] 11.14932 13.15668
[6,] 12.37426 14.58974

Quantos dos IC simulados não contém a verdadeira média populacional?3

Por meio de uma análise gráfica:

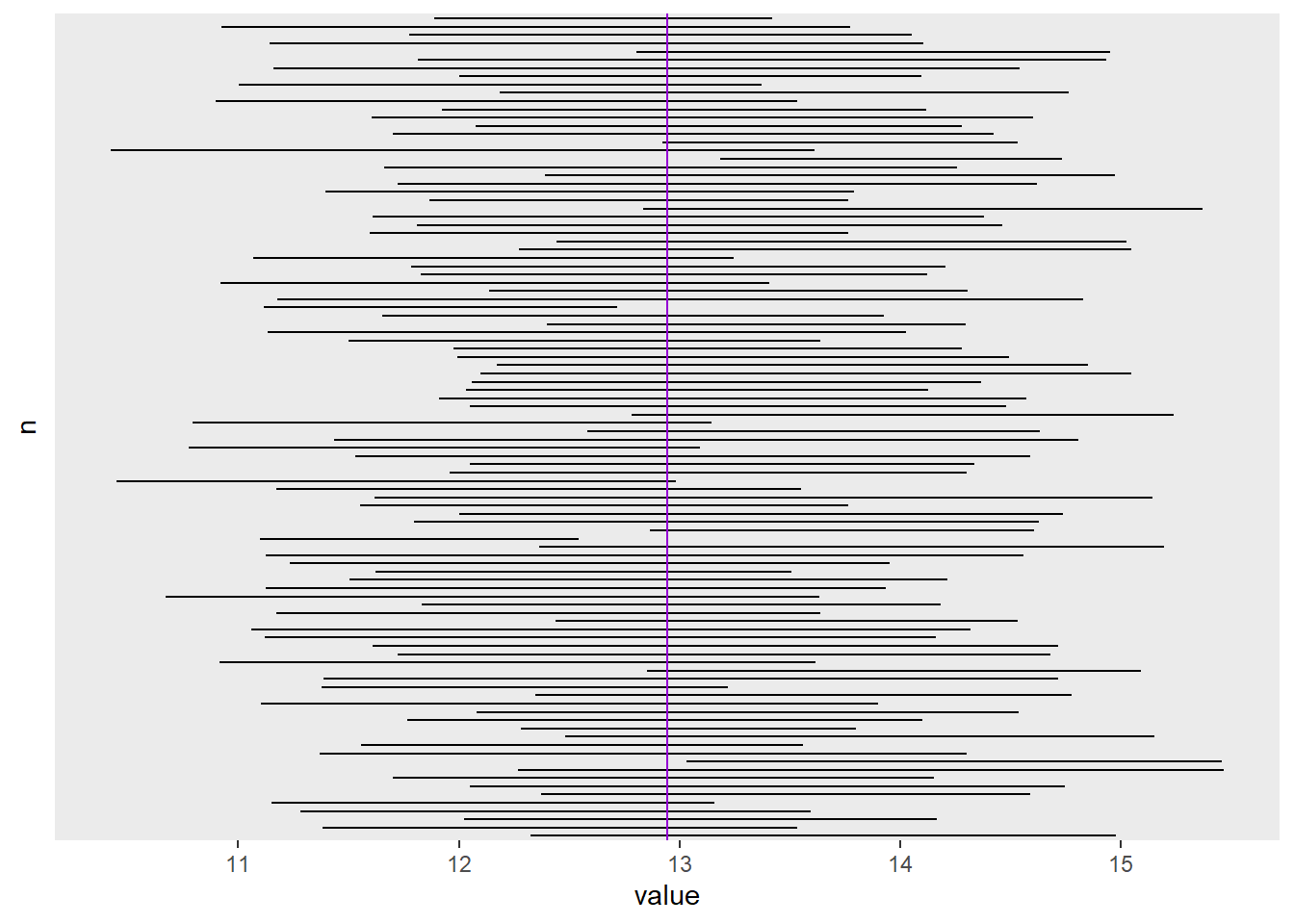
Intervalos de confiança simulados para várias amostragens de uma população. A média populacional é representada pela linha vertical violeta.

Os resultados mostram que 4 dos 100 ICs simulados não contém a média populacional. Para um IC de 95%, está bem próximo do valor esperado.

9.2 O teste t para uma amostra

O teste t para uma amostra é usado para comparar a média de uma amostra com um valor hipotético. Ele permite avaliar se a diferença observada entre a média da amostra e o valor hipotético é estatisticamente significativa ou se pode ser atribuída ao acaso, ou seja, avalia a evidência a favor ou contra uma hipótese.

Antes de realizar o teste t, é importante formular as hipóteses que serão testadas:

  • Hipótese nula (H0): A hipótese nula é uma afirmação sobre a população que se assume ser verdadeira até que haja evidências suficientes para rejeitá-la. No teste t para uma amostra, a hipótese nula geralmente afirma que a média da população é igual a um valor específico.

  • Hipótese alternativa (H1 ou Ha): A hipótese alternativa é uma afirmação que contradiz a hipótese nula. Ela pode ser formulada de três maneiras:

    • Teste bilateral: A hipótese alternativa afirma que a média da população é diferente do valor especificado na hipótese nula.
    • Teste unilateral à direita: A hipótese alternativa afirma que a média da população é maior que o valor especificado na hipótese nula.
    • Teste unilateral à esquerda: A hipótese alternativa afirma que a média da população é menor que o valor especificado na hipótese nula.

Para tomar uma decisão sobre a hipótese nula, comparamos o valor de p com um nível de significância (α) definido previamente. O valor de α mais comum é 0,05 (5%), mas pode variar dependendo da área de estudo e das consequências de se tomar uma decisão errada.

  • Se o valor de p for menor que α, rejeitamos a hipótese nula.
  • Se o valor de p for maior ou igual a α, não rejeitamos a hipótese nula.

O valor de p é uma medida da evidência contra a hipótese nula. Ele representa a probabilidade de obter uma amostra com a média observada (ou mais extrema) se a hipótese nula fosse verdadeira. Quanto menor o valor de p, maior a evidência contra a hipótese nula.

Exemplo 9.3 (Teste t para uma amostra) Considere o conjunto de dados da Seção A.1, cujos dados estão no arquivo mogno_am.csv. Verifique a hipótese de que a média populacional difere de 15 cm.

Primeiramente, devemos estabelecer as hipóteses:

  • H0: esta amostra vem de uma população cuja média populacional é igual a 15 cm.
  • H1: esta amostra vem de uma população cuja média populacional é diferente de 15 cm.

Na função t.test passamos o valor da média da hipótese H0 para o argumento mu.

t.test(mogno_am$dap, mu = 15)

    One Sample t-test

data:  mogno_am$dap
t = -2.8962, df = 9, p-value = 0.01771
alternative hypothesis: true mean is not equal to 15
95 percent confidence interval:
 12.01668 14.63332
sample estimates:
mean of x 
   13.325

A média desta amostra é 13,32 cm. Este valor difere (numericamente) da nossa hipótese, que é de 15 cm. O p-valor do teste (p = 0,0177 nos leva a rejeitar a hipótese H0, ou seja, há evidências de que a média populacional seja estatisticamente diferente de 15 cm.

9.3 Teste t para dados emparelhados

O teste t para dados emparelhados é utilizado para comparar as médias de duas amostras que estão relacionadas de alguma forma. Em um delineamento de dados emparelhados, cada observação em uma amostra está ligada a uma observação específica na outra amostra. Essa relação pode ser devido a:

  • Medidas repetidas: A mesma variável é medida duas vezes no mesmo indivíduo ou objeto, como antes e depois de um tratamento.

  • Pareamento: Indivíduos ou objetos são emparelhados com base em características semelhantes, como idade, sexo ou condição física.

  • Amostras naturalmente emparelhadas: As amostras são compostas por pares de indivíduos ou objetos que têm uma ligação natural, como gêmeos, irmãos ou partes do corpo.

Para realizar o teste t para dados emparelhados, calcula-se a diferença entre as observações em cada par e, em seguida, aplica-se o teste t de uma amostra a essas diferenças. A hipótese nula do teste é que a média das diferenças é igual a zero, o que indica que não há diferença significativa entre as médias das duas amostras.

Exemplo 9.4 (Teste t para dados emparelhados) Considere o conjunto de dados da Seção A.6, em que investigou-se o efeito da altitude sobre a concentração de clorofila em folhas de uma espécie de planta. Para cada planta, foram coletadas duas amostras de folhas, uma da base e outra do topo, e a concentração de clorofila (mg/cm2) foi medida em cada amostra.

Os dados da concentração de clorofila nas folhas estão disponíveis no arquivo clorofila.csv.

Verifique a hipótese de que a concentração de clorofila é maior nas folhas do topo da planta em comparação com as folhas da base.

clorofila <- readr::read_csv("data/clorofila.csv") # Importar os dados
# Realizar o teste t pareado
t.test(clorofila$topo, clorofila$base, paired = TRUE)

    Paired t-test

data:  clorofila$topo and clorofila$base
t = 3.9348, df = 19, p-value = 0.0008892
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
  7.816897 25.583103
sample estimates:
mean difference 
           16.7

O p-valor (p=0,00089) é menor que o nível de significância usual de 0,05, indicando que rejeitamos a hipótese nula.

Há evidências de que a concentração média de clorofila no topo da planta é diferente da concentração média na base.

A concentração média4 de clorofila nas folhas do topo da planta foi de 57,5 mg/cm2. Nas folhas da base, foi de 40,8 mg/cm2.

A média das diferenças entre as concentrações de clorofila no topo e na base é 16,7 mg/cm2, com um intervalo de confiança de 95% de 7,8 a 25,6 mg/cm2. Isso indica que a concentração de clorofila no topo é, em média, maior do que na base.

9.4 Teste t para duas amostras

O teste t para duas amostras é usado para comparar as médias de duas populações independentes. Ele avalia se a diferença observada entre as médias de duas amostras é estatisticamente significativa ou se pode ser atribuída ao acaso.

Exemplo 9.5 (Teste t para duas amostras) Um estudo comparou a biomassa de algas em dois riachos com diferentes níveis de poluição. Amostras de água foram coletadas em cada riacho, e a biomassa de algas (mg/L) foi medida em cada amostra (Seção A.7).

Os dados da biomassa de algas estão disponíveis no arquivo algas.csv.

algas <- read.csv("algas.csv") # Importando os dados
# Realizar o teste t para duas amostras
t.test(biomassa ~ riacho, data = algas)

    Welch Two Sample t-test

data:  biomassa by riacho
t = -15.772, df = 53.607, p-value < 2.2e-16
alternative hypothesis: true difference in means between group Jacare and group Turvo is not equal to 0
95 percent confidence interval:
 -41.88027 -32.43223
sample estimates:
mean in group Jacare  mean in group Turvo 
            30.04375             67.20000

Os resultados do teste t indicam que existe uma diferença significativa na biomassa média de algas entre os dois riachos (p-valor=8,7e-22). Isso significa que a biomassa média de algas no riacho Turvo (média = 67,2 mg/L) é significativamente diferente da biomassa média de algas no riacho Jacaré (média = 30,0 mg/L).

  1. valor padrão da função t.test↩︎

  2. É possível realizar mais simulações, por exemplo, 10 mil↩︎

  3. Este valor já é conhecido: 12,95↩︎

  4. da amostra↩︎